LeetCode_2320_统计防止房子的方式数

最新推荐文章于 2024-12-23 17:00:00 发布

Fitz1318

最新推荐文章于 2024-12-23 17:00:00 发布

阅读量122

点赞数

CC 4.0 BY-SA版权

分类专栏： LeetCode学习之路文章标签： leetcode 算法动态规划

本文链接：https://blog.youkuaiyun.com/Fitz1318/article/details/126361857

LeetCode学习之路专栏收录该内容

307 篇文章

订阅专栏

该博客讨论了一道LeetCode上的动态规划题目，涉及在一条街道两侧放置房屋，要求同一侧不能有两所房子相邻。作者介绍了动态规划的解题思路，并提供了AC代码。动态规划状态转移方程为dp[i] = dp[i-2] + dp[i-1]，最后计算结果时对10^9+7取余。示例中给出了n=1和n=2时的解题过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接

https://leetcode.cn/problems/count-number-of-ways-to-place-houses/

题目描述

一条街道上共有 n * 2 个地块，街道的两侧各有 n 个地块。每一边的地块都按从 1 到 n 编号。每个地块上都可以放置一所房子。

现要求街道同一侧不能存在两所房子相邻的情况，请你计算并返回放置房屋的方式数目。由于答案可能很大，需要对 10^9 + 7 取余后再返回。

注意，如果一所房子放置在这条街某一侧上的第 i 个地块，不影响在另一侧的第 i 个地块放置房子。

示例 1：

输入：n = 1
输出：4
解释：
可能的放置方式：

1. 所有地块都不放置房子。
2. 一所房子放在街道的某一侧。
3. 一所房子放在街道的另一侧。
4. 放置两所房子，街道两侧各放置一所。

示例 2：

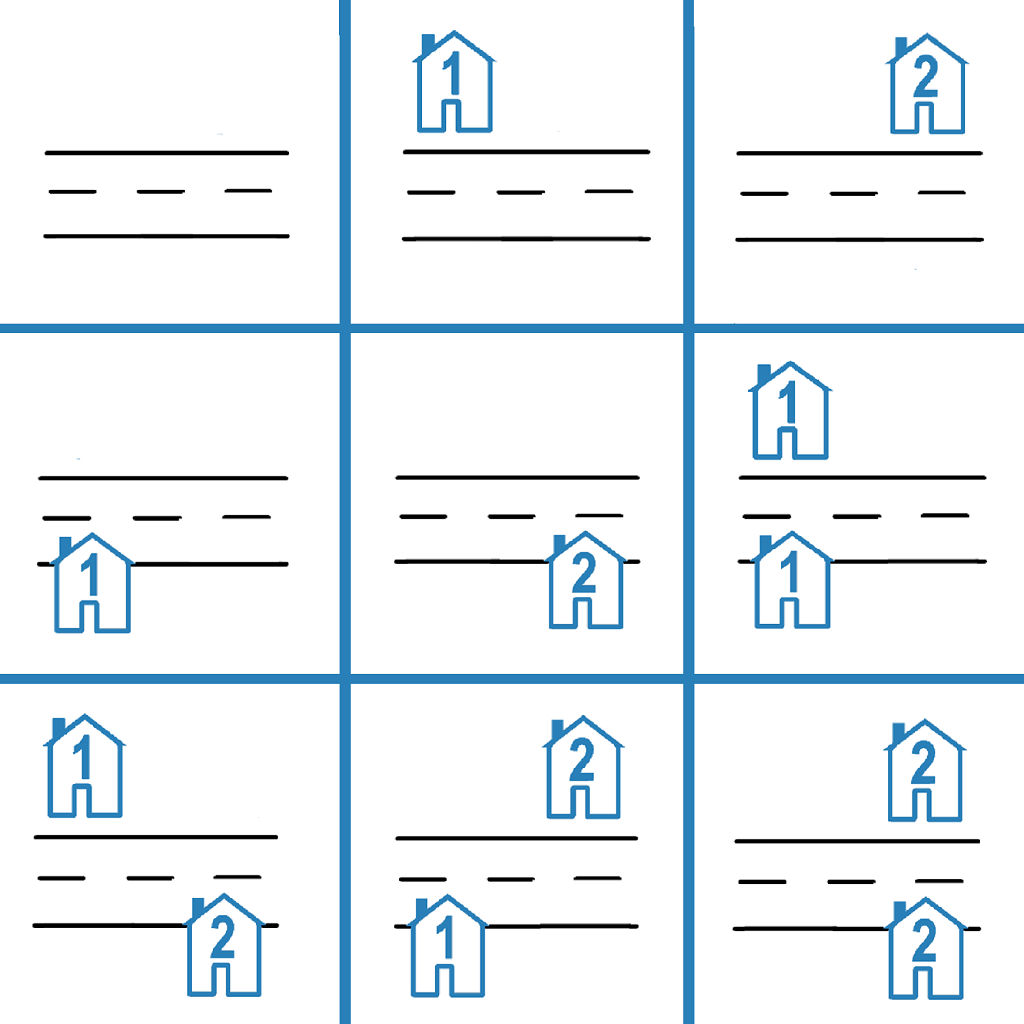
输入：n = 2
输出：9
解释：如上图所示，共有 9 种可能的放置方式。

提示：

1 <= n <= 10^4

解题思路

动态规划法

首先单独考虑一侧的房子，那么这题和打家劫舍就是一样的了。

dp[i]表示前i个土地的放置方案数。

在考虑第i+1块土地时，如果第i块土地有房子，那么第i+1块土地不能放房子，即dp[i + 1] = dp[i]
如果第i块土地没有房子，那么第i-1块可放可不放，即dp[i + 1] = dp[i - 1]
因此dp[i] = dp[i - 1] + dp[i - 2]

AC代码

class Solution {
    public int countHousePlacements(int n) {
        if (n == 0) {
            return 1;
        }
        if (n == 1) {
            return 4;
        }
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 2;
        for (int i = 2; i <= n; i++) {
            dp[i] = (dp[i - 2] + dp[i - 1]) % 1000000007;
        }
        return (int) ((long) dp[n] * dp[n] % 1000000007);
    }
}