LeetCode_96_不同的二叉搜索树

最新推荐文章于 2025-12-17 23:41:09 发布

原创最新推荐文章于 2025-12-17 23:41:09 发布 · 142 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #数据结构 #动态规划

LeetCode学习之路专栏收录该内容

307 篇文章

订阅专栏

这篇博客探讨了如何使用动态规划方法解决LeetCode上的第98题——「不同的二叉搜索树」。博主详细解释了二叉搜索树的定义，并通过示例1和示例2展示了解题思路。通过递推公式`dp[i]+=dp[j-1]*dp[i-j]`，博主展示了如何计算给定节点数n的不同二叉搜索树的数量，最终给出了AC代码实现。

题目链接

https://leetcode.cn/problems/unique-binary-search-trees/

题目描述

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

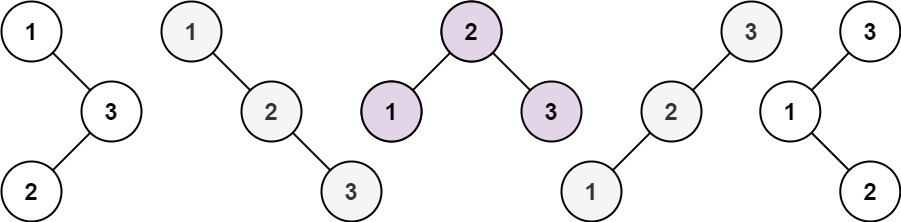
输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

提示：

1 <= n <= 19

解题思路

动态规划法

首先明确一下二叉搜索树的定义：它或者是一棵空树，或者是具有下列性质的二叉树：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉排序树。

以示例1为例子，dp[3]就是以元素1为根节点的二叉搜索树数量+元素2为根节点的数量+元素3为根节点的数量。并且根据二叉搜索树的定义，可以有如下总结：

1为根节点的数量 = 左子树有0个元素的数量 * 右子树有2个元素的数量
2为根节点的数量 = 左子树有1个元素的数量 * 右子树有1个元素的数量
3为根节点的数量 = 左子树有2个元素的数量 * 右子树有0个元素的数量
重点：有2个元素的数量为dp[2]，有1个元素的数量为dp[1]

因此可以得出dp[3] = dp[0] * dp[2] + dp[1] * dp[1] + dp[2] * dp[0],归纳一下可以得到

dp[i] += dp[j-1] * dp[i-j]

其中j相当于根节点，从1遍历到i为止.j-1为j为根节点的左子树节点数量，i-j为右子树节点数量

AC代码

class Solution {
    public int numTrees(int n) {
        if(n == 1){
            return 1;
        }
        int[] dp = new int[n+1];
        dp[0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <=i ; j++) {
                dp[i] += dp[j-1] * dp[i-j];
            }
        }
        return dp[n];
    }
}