李宏毅机器学习三天速成~~~第六课~~~Logistic Regression

1.Function Set

利用概率模型进行分类，分类的判别方法和分类判别模型如下所示：

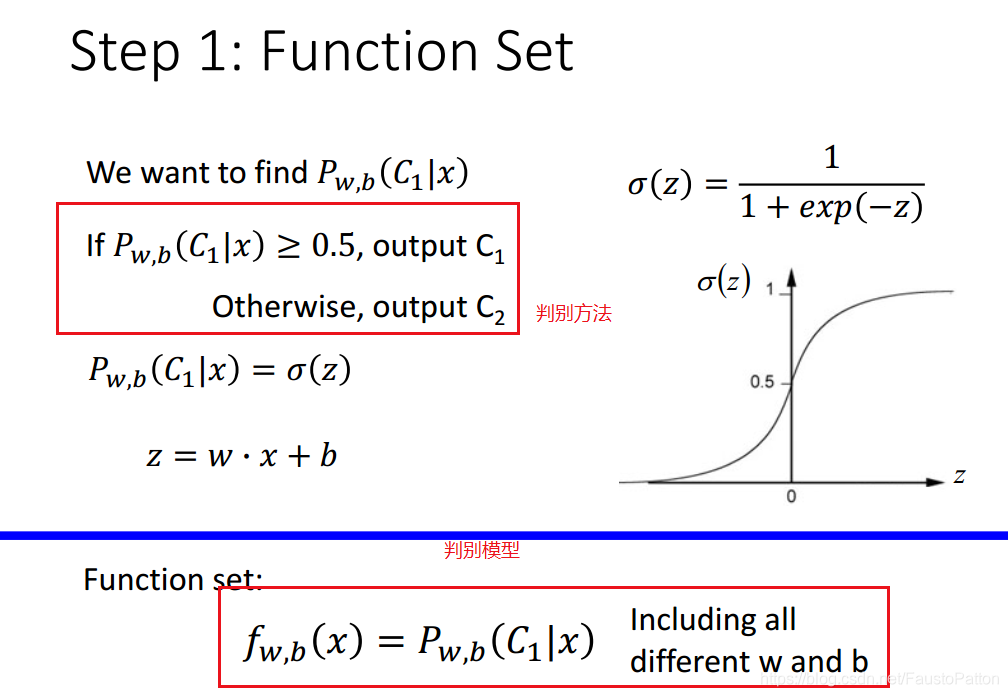
判别的模型采用的是sigmoid function。

Sigmoid函数的输入记为z，由下面公式得出

它表示将这两个数值向量对应元素相乘然后全部加起来即得到z值。其中的向量x是分类器的输入数据，向量w也就是我们要找到的最佳参数（系数），从而使得分类器尽可能地精确。

Sigmoid输出的值即为几率。可以用下图表示：

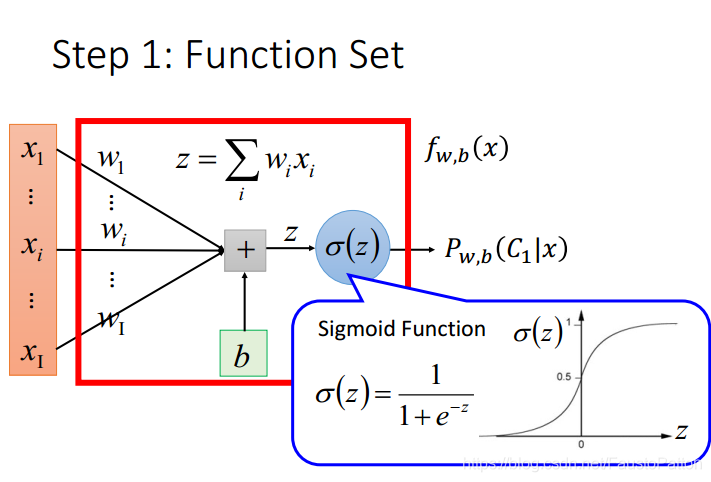
以上模型就是Logistic Regression。

2.判别Logistic Regression的好坏程度：

注意不同的class表达的公式不同

以上参数w,b的最优结果就是使得likeihood最大的参数，即 使L（w,b）最大的参数。

下面用数字代替class1,class2,同时对w,b的表达式进行替换。

总结以上得到：

对model的likeihood进行转换，由求使L（w,b）最大的w,b，改为求使-ln(w,b)最小的w,b,而化简-ln(w,b)的结果表示-ln(w,b)则为求

两个伯努利分布的交叉熵cross entropy。

所谓交叉熵，是用来刻画两个分布的相似性。在这里，交叉熵可以理解为真实分布与预测分布的相似度。同分布的话，交叉熵是0。

对Logistic Regression和Linear Regression进行对比分析，可以得到：

注意，下图左边的L（f）为交叉熵，同时可以作为Loss Function，而不是Likelyhood

上图中提出一个问题，就是为什么不用square error用于计算Logistic Regression的error.

3.Find the best function

主旨思想：利用Gradient decent求使-lnL(w,b)最小的w,b。

下面是一些求微分的相关的数学计算：

注意Sigmoid函数的微分等于

对比一下Logostic Regression和Linear Regression中的Gradient Descent可以发现两个方法很相似。

问题：为什么不用Square error去计算Loss function?下面进行尝试一下：

首先利用square error作为Loss function,并对者求微分，下面用两种情况来论述一下：

第一种情况：

y的实际值为1时，如果sigmoid函数值为1（很接近目标值），其微分结果为0

y的实际值为1时，如果sigmoid函数值为0（距离目标值很远），其微分值还是为0，那么在Gradient Descent过程中将会卡住，无法移动。这种情况见下图

第二种情况时y的实际值为0时的实验，同理并见下图：

下面对比cross Entroy和square error作为Loss Function的两种情况下的差异：

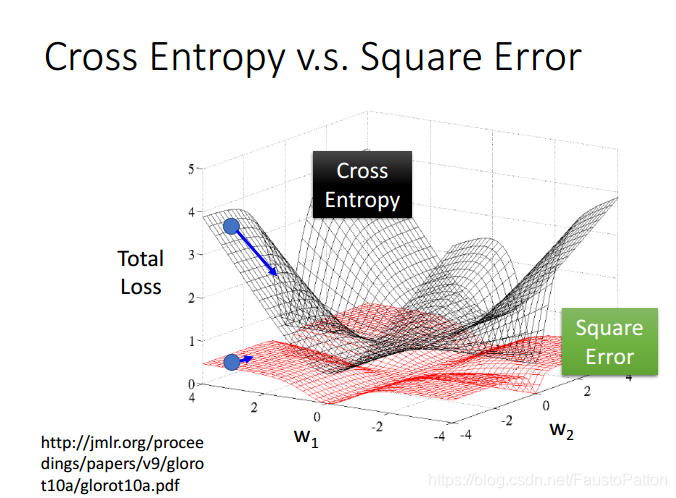
上图中可以发现，cross entropy距离目标值远的时候，下降速度很快，然而square error距离目标值很远的时候，微分值十分小，下降速度很慢，对实际实验很浪费时间，不容易得到结果。所有要使用cross entropy作为Loss Function。

2.Discriminative v.s. Generative（判别模型vs生成模型）

Logistic Regression是Discriminative model

利用Gaussian Distribution的则是Generative model

两个其实本质上没有区别，function set都是一样的，如下图所示：

上图中可以发现计算参数的方法不一样，得到的参数也不一样，但是哪一个比较好呢？

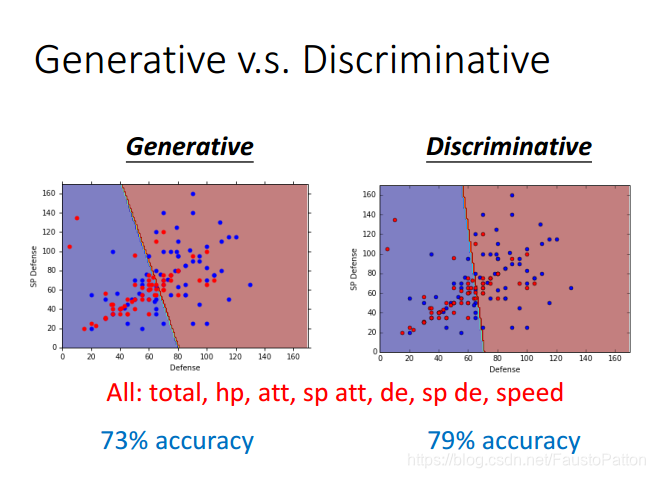
事实上Discriminative model比Generative model的效果要好。

下面对为什么会好进行解释一下：

上图中，每个数据中拥有两个特征,有两种类型，通过对Training data进行分析判别Testing data属于那种类型。

下面利用naive Bayes进行判别，发现判别testing的数据居然属于Class2

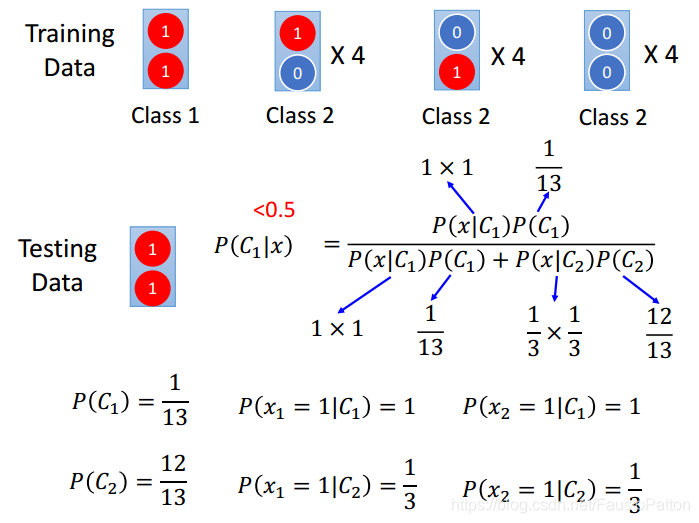
这是因为样本数量不够多

关于Generative model与Discriminative model的区别就是Generative model由做出一种假设，假设数据满足某种几率模型，即脑补。Discriminative model则没有做出任何假设。

Generative model的优势：数据量少的时候有优势，不受数据量影响。

Discriminative model的优势：数据量多的时候error越小，model越准确。

3.Multi-class Classification

和两个类别的分类相似。

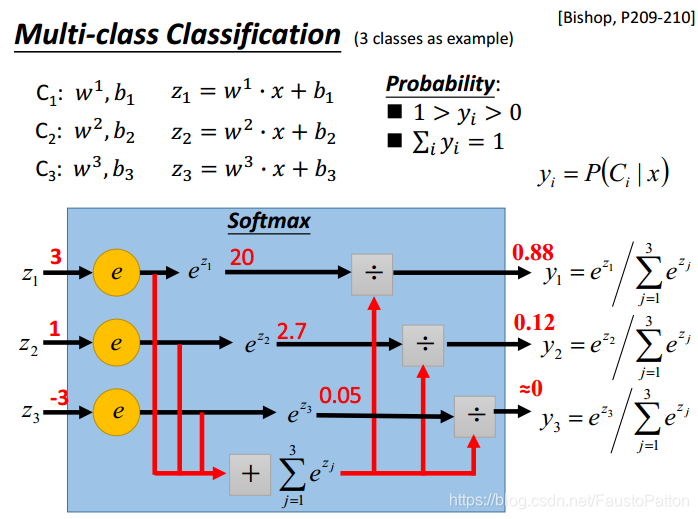
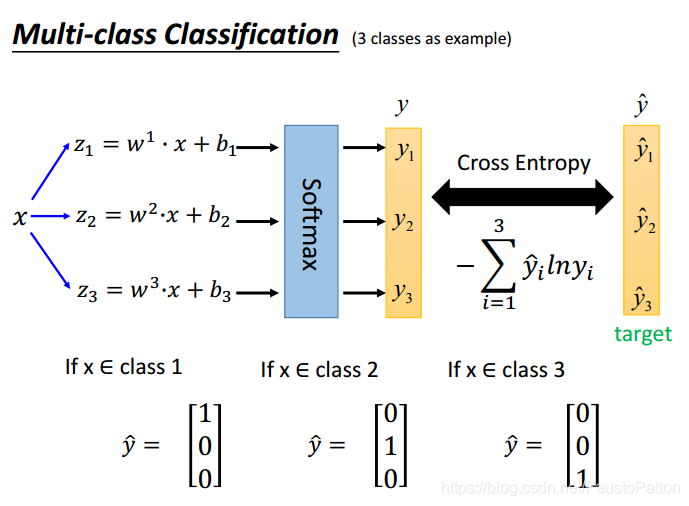
4.Limitation of Logistic Regression

Logistic Regression的不同类之间的分界线是一条线，永远画不了两条线。比如

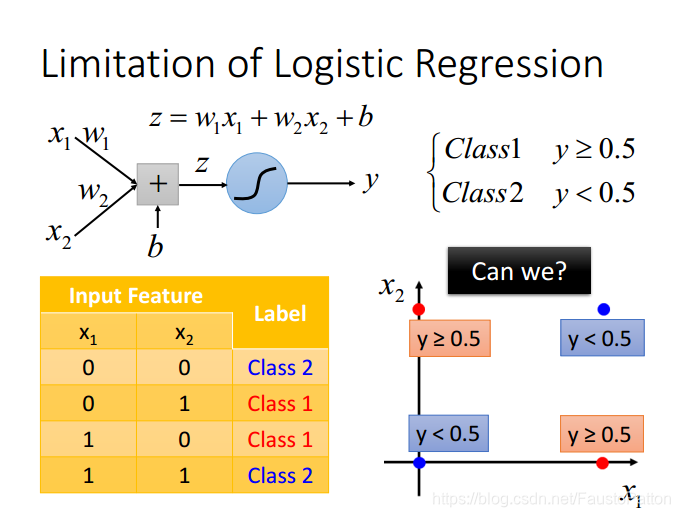
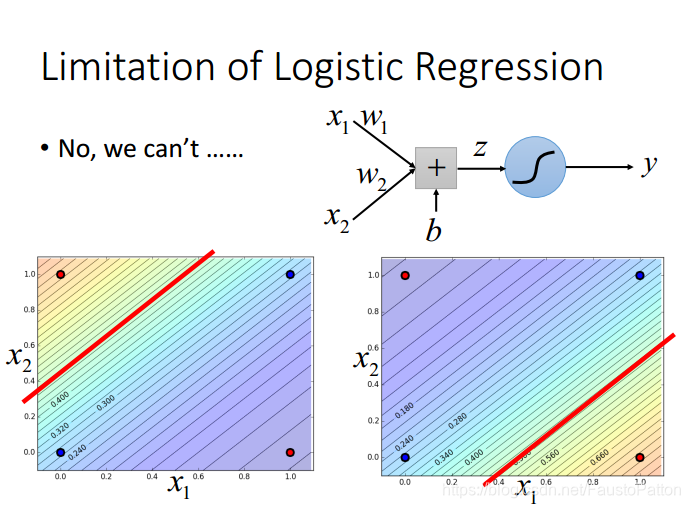
关于这类问题可以利用Feature Transformation，但是Feature Transformation并不是那么简单的！

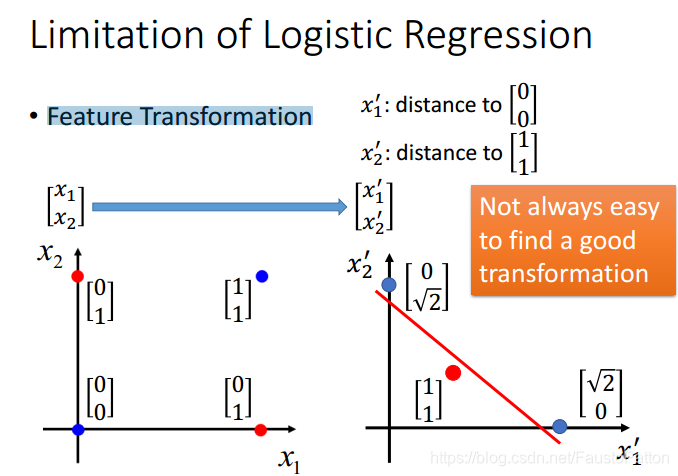
那么做法呢？利用多个Logistic Regression进行叠加。

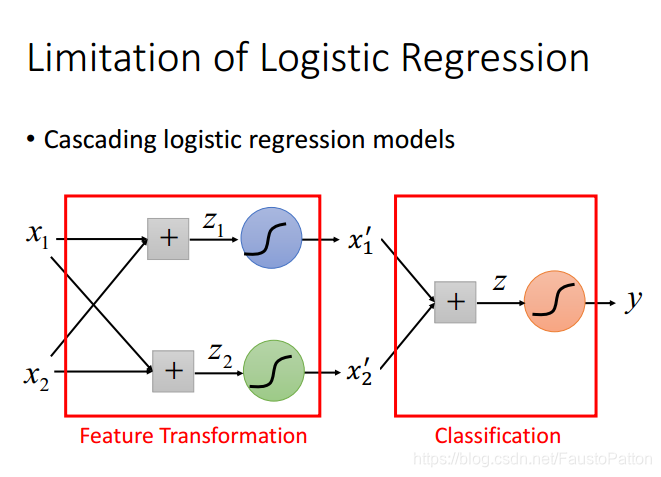
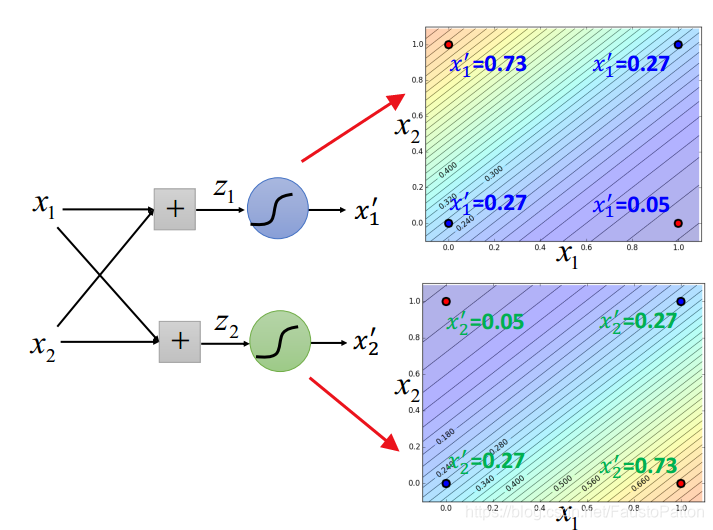
下面就可以用一条线进行分类了（注意下图右边图中的坐标系弄反了）

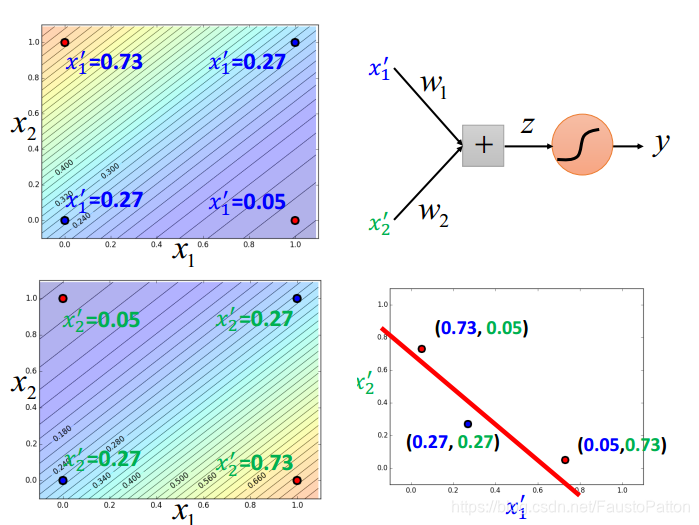
然后装下逼，这个就类似神经网络了，名词很牛逼吧，可以骗人了。

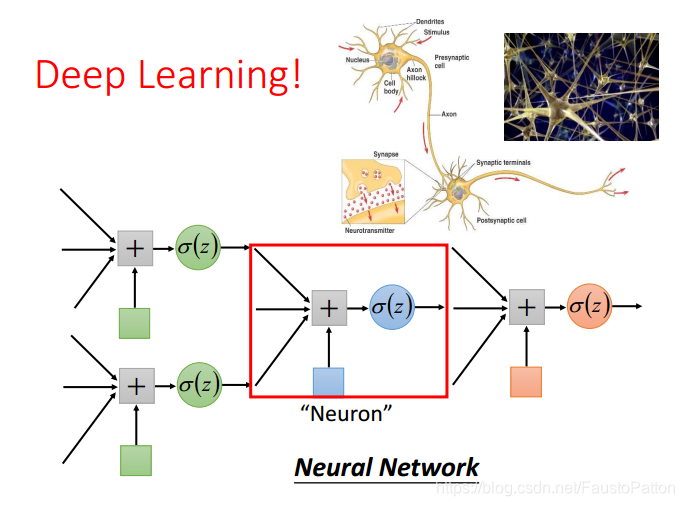
个人理解性内容将后续补充。