重建二叉树

在做题目的时候，做到通过前序遍历和中序遍历或则中序遍历和后序遍历的序列，来重新构建二叉树，并且返回根节点。如果做过剑指offer的题目的同学，应该做过这道题。
首先呢，我们先来熟悉一个前序遍历，中序遍历和后序遍历的顺序吧。
前序遍历：根节点，左孩子，右孩子
中序遍历：左孩子，根节点，有孩子
后序遍历：左孩子，有孩子，根节点
可以看出，可以根据根节点的所在位置来称呼遍历的顺序，这也是做这道题目的关键所在。
那么下面就开始实战吧。
已知一个二叉树的前序遍历序列是{1，2，4，7，3，5，6，8}，中序遍历的序列是{4，7，2，1，5，3，8，6}，要求重建二叉树，并且输出它的头节点。二叉树的节点定义如下：

//定义二叉树的节点
    public class TreeNode {
        int val;
        //定义树的节点，左节点和右节点
        TreeNode left;
        TreeNode right;
        TreeNode(int x){
            val = x;
        }
    }

首先理论分析一下吧。根据前序遍历和中序遍历的特点，可以知道前序遍历序列的第一个元素就是根节点，那么在中序遍历序列中，根节点的左边是左子树，右边是右子树。根据这个特性，就可以利用递归来分别构建左右子树。
代码如下：

//前序加中序遍历
    //前序遍历{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}
    //传入的参数：前序遍历的数组，前序遍历的起点索引，
    //前序遍历的终点的索引， 中序遍历的数组， 中序遍历的起点索引，
    //中序遍历的终点索引
    //索引就是在数组中的位置
    private TreeNode reConstructBinaryTree(int[] preorder,int startPreorder, int endPreorder,
                                            int [] inorder, int startInorder, int endInorder){
        //如果数组不存在，即二叉树不存在。返回空
        if(startPreorder > endPreorder || startInorder > endInorder)
            return null;

        //前序遍历的起点就是二叉树的根节点，可以说startPreorder就是0
        TreeNode root = new TreeNode(preorder[startPreorder]);

        //遍历中序遍历数组的所有元素，根据所给的例子就是从遍历从0到7
        for(int i=startInorder; i<= endInorder; i++){
            //如果中序遍历的数组元素中有等于等节点值的，即为根节点，根节点的索引为3
            if(inorder[i] == root.val){
                //构建左子树 在左子树中，前序遍历中，起点的索引是1，
                //值是2，终点索引是3，值是7；在中序遍历中，起点的索引是9，
                //值是4，终点的索引是2，值是2
                root.left=reConstructBinaryTree(preorder,startPreorder+1, startPreorder
                        +i - startInorder, inorder, startInorder, i-1);

                //由于中序遍历的特性，根节点左边的节点为左孩子部分，右边为右孩子部分
                //构建右子树，在右子树中，前序遍历中，起点的索引是4，
                //值是7，终点的索引是7，值是8； 在中序遍历中，
                //起点的索引是4，值是5，终点的索引是7，值是6，
                //然后调整相应的参数
                root.right=reConstructBinaryTree(preorder,i-startInorder+startPreorder+1,
                        endPreorder, inorder,i+1, endInorder);
                break;
            }
        }
        return root;
    }

public TreeNode reConstructBinaryTree(int [] preorder, int [] inorder) {
        TreeNode root = reConstructBinaryTree(preorder,0,preorder.length-1,inorder,
                0, inorder.length-1);
        return root;

    }

只要把定义函数和主函数加上，再输入相应的前序和终须遍历序列就能重新构造二叉树，并且输出头节点。
我的主函数是这样的，直接输出的是头节点的值，再这组数组中也就是1

public static void main(String[] args) {
        int[] preorder = new int[]{1, 2, 4, 7, 3, 5, 6, 8};
        int[] inorder = new int[]{4,7,2,1,5,3,8,6};

        Solution sn = new Solution();
        System.out.println(sn.reConstructBinaryTree(preorder,inorder).val);
    }

那么我们核对一下答案，根据剑指offer的题目的信息，可以得到完整的二叉树结构是这样的。

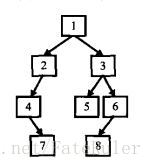
可以看到根节点的值是1.

那么下面我们再扩展一下，如果条件变成已知中序遍历和后序遍历序列，然后再做这道题目呢，其实差别并不大，对上面的代码稍作修改即可。主要的改变来自于，后序遍历序列的最后以为是头节点的数值，这与前序遍历序列第一位是头节点的数值，区别。

//中序遍历加后序遍历
    //中序遍历数组{4，7，2， 1， 5，3，8，6}，后序遍历数组{7，4，2， 8，5，6，3， 1}
    //传入的参数：后序遍历的数组，前序遍历的起点索引，
    //前序遍历的终点的索引， 中序遍历的数组，
    // 中序遍历的起点索引，中序遍历的终点索引
    private TreeNode reConstructBinaryTree(int[] afterorder, int startafterorder, int endafterorder,
                 int [] inorder, int startInorder, int endInorder){
        //如果数组不存在，即二叉树不存在。返回空
        if(startafterorder > endafterorder || startInorder > endInorder)
            return null;

        //后序遍历的终点就是二叉树的根节点，可以说endafterorder就是7,值是1，修改一下
        TreeNode root = new  TreeNode(afterorder[endafterorder]);

        //遍历中序遍历数组的所有元素，根据所给的数组就是从遍历从0到7
        for(int i=startInorder; i<= endInorder; i++){
            //如果中序遍历的数组元素中有等于等节点值的，即为根节点，根节点的索引为3
            if(inorder[i] == root.val){
                //构建左子树 在左子树中，后序遍历中，起点的索引是0，
                //值是7，终点索引是2，值是2；在中序遍历中，
                //起点的索引是0，值是4，终点的索引是2，值是2（修改一下）
                root.left=reConstructBinaryTree(afterorder, startafterorder, i - startInorder+startafterorder-1,
                        inorder, startInorder,i-1);

                //由于中序遍历的特性，根节点左边的节点为左孩子部分，右边为右孩子部分
                //构建右子树，在右子树中，后序遍历中，起点的索引是3，
                //值是8，终点的索引是6，值是3； 在中序遍历中，起点的索引是4，
                //值是5，终点的索引是7，值是6（修改一下）
                root.right=reConstructBinaryTree(afterorder,i-startInorder+startafterorder,
                        endafterorder-1, inorder,i+1, endInorder);
                break;
            }
        }
        return root;
    }

有的人可能会问，为什么你不说前序遍历和后序遍历来重构二叉树呢？其实只有前序和后序遍历序列是不能一维确定二叉树的，所以这里就没有讨论了。