【JZOJ 5771】【NOIP2008模拟】遨游 (最短路+二分)

问题描述
MWH寒假外出旅游，来到了S国。S国划分为N个省，第i个省有Ti座城市，编号分别为Ci1，Ci2，……CiTi（各省城市编号不会重复）。所有城市间有M条双向的道路连接，从任意一个城市出发，可到达一切城市，每条道路均须收费。
此时恰逢春运期间，S国交通运输局采取了优惠措施。当一条路的路费在[L..R]区间时，可免去。同时，每个省也有优惠措施，第i个省内的每条道路路费收其Xi%，连接第i个省和第j个省的每条道路路费收其(Xi%+Xj%)/2。
MWH想从城市s走到城市t，请求出一对L，R，确保：

MWH能免费到达目的地；
L≤R；
L、R均为整数；
L尽可能地大，R在满足L最大的前提下最小。

注意：因每条道路由各省的交通运输局直接管辖，所以每条道路的路费必须先得到省级优惠，再得到国家级优惠
输入
第一行两个整数N，M。
接下来M行，每行三个整数，u、v、w，表示连接u、v的道路需收费w。
接下来N行，第i+M+1行有一个整数Ti，后面Ti个整数，分别是Ci1..CiTi（所有城市编号保证按正整数顺序给出1.. Ti）。
下一行N个整数X1..Xi。
最后一行，两个整数，s、t。
输出
一行两个整数，如题，L和R。
样例输入
3 7
1 2 3
5 2 8
1 3 7
5 4 5
2 4 9
3 5 10
3 4 2
2 1 2
1 3
2 4 5
30 50 60
1 5
样例输出
2 6

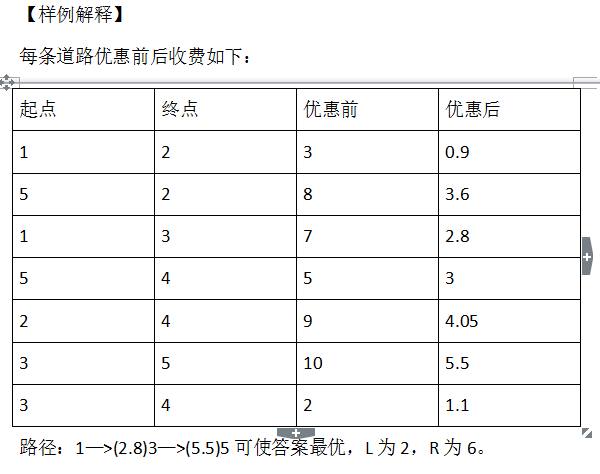
算法讨论
对于题目描述中既有“最大”又有“最小”的题目，很多都是用二分，这题也不例外。
首先，省级路费是很容易算且是独立的，所以预处理出每条道路经过了省级优惠后是多少路费。
然后我们分别用两个二分处理出L和R，第一个二分先处理出L，如果当前l1,r1可以到达目的地，就把l1开大，否则r1减小。第二个二分处理R，加上之前处理出的L的限制，如果当前l1,r1可以到达目的地，就把r1减小，否则l1开大。

#include <cstdio>
#include <deque>
#define MAX_N 5006
#define MAX_T 50006
#define MAX_M 100006
#define maxlongint 0x3f3f3f3f
using namespace std;
struct edge
{
    int f,t,n;
    double w;
}a[MAX_M*2];
int ls[MAX_T],c[MAX_T],n,m,s,t,l,T,L=maxlongint,R,l1,r1,mid,mid1,sl,sr;
bool v[MAX_T];
double X[MAX_N],d[MAX_T],dist[MAX_T];
deque <int> q;

void init()
{
    scanf("%d%d",&n,&m);
    for (int i=1;i<=m;i++)
    {
        l++;
        scanf("%d%d%lf",&a[l].f,&a[l].t,&a[l].w);
        a[l].n=ls[a[l].f];
        ls[a[l].f]=l;
        a[++l].f=a[l-1].t; a[l].t=a[l-1].f; a[l].w=a[l-1].w;
        a[l].n=ls[a[l].f];
        ls[a[l].f]=l;
    }
    int x,y,p=0;
    for (int i=1;i<=n;i++)
    {
        scanf("%d",&x);
        T+=x;
        for (int j=1;j<=x;j++)
        {
            scanf("%d",&y);
            c[++p]=i;
        }
    }
    for (int i=1;i<=n;i++)
    {
        scanf("%lf",&X[i]);
        X[i]/=100;
    }
    scanf("%d%d",&s,&t);
    p=0;
    for (int i=1;i<=m;i++)
    {
        p++;
        if (c[a[p].f]==c[a[p].t])
        {
            a[p].w*=X[c[a[p].t]];
            a[++p].w=a[p-1].w;
        }
        else
        {
            a[p].w*=((X[c[a[p].f]]+X[c[a[p].t]]) / 2);
            a[++p].w=a[p-1].w;
        }
        if (a[p].w<L)
            L=a[p].w;
        if (a[p].w>R)
            R=a[p].w;
    }
    R++;
}

bool spfa(int l,int r)
{
    for (int i=1;i<=T;i++)
        d[i]=maxlongint;
    d[s]=0; v[s]=1;
    q.push_back(s);
    while (!q.empty())
    {
        int u=q.front();
        q.pop_front(); v[u]=0;
        for (int i=ls[u];i;i=a[i].n)
            if (d[u]+a[i].w<d[a[i].t] && a[i].w>=l && a[i].w<=r)
            {
                d[a[i].t]=d[u]+a[i].w;
                if (!v[a[i].t])
                {
                    v[a[i].t]=1;
                    if (q.empty() || d[a[i].t]>d[q.front()])
                        q.push_back(a[i].t);
                    else
                        q.push_front(a[i].t);
                }
            }
    }
    if (d[t]!=maxlongint)
        return 1;
    return 0;
}
int main()
{
    freopen("trip.in","r",stdin);
    freopen("trip.out","w",stdout);
    init();
    int L1=L,R1=R;
    while (L1<=R1)
    {
        mid=(L1+R1) / 2;
        if (spfa(mid,R))
        {
            L1=mid+1;
            sl=mid;
        }
        else
        {
            if (L1==R1)
                break;
            R1=mid;
        }
    }
    l1=sl; r1=R;
    while (l1<=r1)
    {
        mid1=(l1+r1) / 2;
        if (spfa(sl,mid1))
        {
            r1=mid1;
            sr=mid1;
            if (l1==r1)
                break;
        }
        else
            l1=mid1+1;
    }
    printf("%d %d",sl,sr);
    fclose(stdin); fclose(stdout);
}