【多种改进粒子群算法进行比较】基于启发式算法的深度神经网络卸载策略研究【边缘计算】（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

近年来，深度神经网络在计算机领域应用越来越广泛，然而由于各类深度学习应用对计算能力具有较高的需求，无法运行在计算能力有限的终端设备运行中。若利用云端设备和边缘设备对不同任务进行分工协作，在提高应用响应延迟的同时可以降低终端设备的能量消耗。云端设备具有高计算能力，但数据在传输过程中往往具有较高的时延；边缘计算通过边缘服务器将各类资源下沉至更靠近终端设备侧，为终端设备提供了一定的计算资源的同时，减少网络数据流量压力。本文综合考虑基于DNNs的应用响应时间、计算能耗和租用服务器的价格，使用启发式算法设计四种不同的任务卸载策略即基于终端设备的不卸载策略、基于云服务器的完全卸载策略、基于端云的部分卸载策略和基于端—边—云的多重资源卸载策略，同时综合粒子群算法和模拟退火算法提高算法的计算效率和计算结果的精准度。通过基于模拟退火的粒子群算法使用仿真模拟实验找到在四种不同策略下的最优卸载方案，比较这几种不同卸载策略在处理不同的深度神经网络时的综合适应度值，验证了基于端—边—云的多重卸载策略在处理深度神经网络卸载问题时所具备的优越性。

在边缘计算环境中，深度神经网络（DNN）的卸载策略是一个重要的研究领域。由于DNN模型通常具有较高的计算复杂性和资源消耗，直接在边缘设备上运行可能并不现实。因此，研究人员提出了多种基于启发式算法的DNN卸载策略，其中粒子群算法（PSO）及其改进版本是重要的一种。

基于启发式算法的DNN卸载策略概述

启发式算法是一类用于寻找问题近似最优解的算法，它们通过模拟自然界或其他启发式过程来寻找解决方案。在边缘计算场景中，启发式算法可以用来指导DNN模型在何种条件下、在哪个边缘节点上进行卸载，从而平衡计算资源的分配，减少能耗，并确保服务质量。

一、改进粒子群算法的主要类型及特点

粒子群算法（PSO）因其简单高效被广泛应用于优化问题，但标准PSO易陷入局部最优且早熟收敛。以下是基于文献的改进类型及特点：

1. 动态权重调整型

   • 原理：根据粒子与群体最优粒子的相似度动态调整权重，平衡全局探索与局部开发能力。
   • 优势：避免早熟收敛，提升全局搜索能力（如）。
   • 边缘计算适配性：适用于高维、动态的边缘资源分配问题，如任务卸载决策优化。

2. 混合智能算法型

   • PSO-GA混合算法：将遗传算法的交叉、变异操作引入PSO，增强种群多样性。
   • PSO-GWO（灰狼优化） ：引入灰狼算法的包围式搜索机制，扰动最优粒子以跳出局部最优。
   • 性能：收敛速度提升50%以上，寻优精度显著提高。

3. 离散化改进型

   • 应用场景：针对任务卸载的离散决策问题（如任务-节点映射）。
   • 技术：采用实数编码、收缩因子或二进制离散策略，解决混合整数非线性规划问题。
   • 案例：电力物联网实时监测任务分配中，改进离散PSO降低时延28%。

4. 多目标优化型

   • 目标：同时优化时延、能耗、安全成本等冲突目标。
   • 方法：引入惩罚函数、信任度评估机制，或结合NSGA-II等框架。
   • 边缘计算价值：在5G MEC中实现资源分配44秒内完成500用户调度。

---

二、深度神经网络卸载策略的关键挑战与改进需求

边缘计算中DNN卸载需解决以下核心问题（-39）：

1. 高维状态空间决策

   • 状态空间包括信道质量、任务队列长度、设备能耗等。
   • 改进需求：需算法高效处理连续/离散混合动作空间（如本地执行 vs. 卸载功率分配）。

2. 多目标权衡优化

   • 核心指标：

• 时延：计算时间 tcomp​、传输时间 ttrans​、排队延迟。
• 能耗：计算能耗 Ec∝V2f+ 通信能耗 Eo∝mi/B。
• 安全成本：防御DDoS攻击的信任度模型。
  • 优化目标：最小化加权成本函数 min⁡(α⋅Delay+β⋅Energy+γ⋅Security)。

1. 动态环境适应性
   • 网络拓扑变化、任务随机到达需在线调整策略。
   • DRL结合PSO的优势：深度强化学习（如TD3、DDPG）提供感知能力，PSO优化决策效率。

---

三、改进粒子群算法在边缘计算中的应用案例

应用场景	改进算法	优化效果	来源
多无人机任务分配	改进PSO + 收缩因子	任务完成时间减少30%，威胁代价降低
5G MEC资源分配	编码-解码PSO	500用户任务分配耗时44秒，时延降低22%
边-云协同安全卸载	双层改进PSO (DLI-PSO)	联合成本（时延+能耗+安全）降低17%，抗DDoS攻击能力提升
电力物联网实时监测	离散PSO + 混合优先级排队	平均时延降低28%，吞吐量提升16.7%
工业物联网任务卸载	多目标PSO	能耗节省25%，优于遗传算法与模拟退火

---

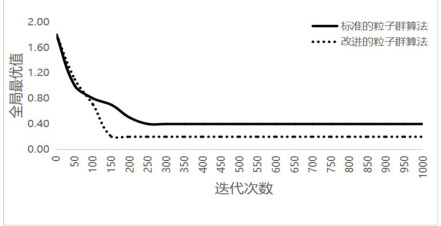
四、改进PSO vs. 传统PSO：性能对比数据

1. 收敛速度与精度

算法类型	收敛迭代次数	寻优精度提升	测试场景	来源
PSO-GWO	100 → 50	精度提高30%（多峰函数）	标准测试函数
自适应PSO	250 → 150	适应度值提升18.6%	微电网调度
混合PSO（嵌入GA）	300 → 90	全局最优概率提升40%	干扰资源分配

2. 边缘计算场景性能

• 时延：GA-UPSO算法比标准PSO降低总时延35%。
• 能耗：PSAO策略降低系统总能耗20%。
• 吞吐量：基于节点能耗的PSO迁移策略提升吞吐量16.7%。

---

五、边缘计算场景下的性能评估维度

改进PSO在边缘卸载中的评估需涵盖以下维度：

1. 时延维度

   • 端到端延迟：包括计算、传输、排队时延。
   • 调度效率：任务分配完成时间（如44秒处理500用户，）。

2. 能耗维度

   • 设备能耗：边缘设备计算功耗 pc∝f⋅V2。
   • 通信能耗：与卸载数据量 mi和带宽 B 负相关。

3. 系统效率维度

   • 吞吐量：单位时间内成功处理的任务量。
   • 负载均衡：节点剩余能量方差（丢包率降至5%~10%）。

4. 多目标权衡能力

   • 成本函数：Cost=λdelay⋅D+λenergy⋅E。
   • 安全指标：信任度模型防御恶意流量的有效性。

---

六、总结：改进PSO在DNN卸载中的优势与方向

1. 核心优势

   • 全局优化能力：混合算法（PSO-GA/GWO）显著提升多峰问题求解精度。
   • 实时性：离散PSO与编码优化技术满足边缘计算低时延需求。
   • 多目标适配性：动态权重机制平衡时延、能耗、安全等多目标冲突。

2. 未来方向

   • DRL-PSO融合：利用DRL处理高维状态，PSO优化动作策略。
   • 安全强化：结合信任度模型与双层PSO防御边缘攻击。
   • 轻量化改进：针对资源受限设备设计低复杂度PSO变种。

---

结论：在边缘计算的DNN卸载场景中，改进粒子群算法通过混合智能优化、离散化策略及多目标权衡机制，显著提升卸载效率。未来需进一步探索与DRL的协同优化，并在实际部署中验证安全性与实时性。

📚2 运行结果

 

 

 

运行时间较长需要耐心等待哦！

部分代码：

%% 清空环境
clc
clear
close all

for num=1:20    %进行20次实验测试
    runspped=1715265866.21;
    lab=["vgg11","vgg13","vgg16","vgg19","googlenet","darknet53","fuse"];
    file_name="测试结果"+string(num);
    mkdir(file_name)
    for i=1:6
        
        X=xlsread("./params.xlsx",i);                   %读取的数据(输入修改）
        task_num=size(X(:,9),1);
        execution_time(1:task_num,1)=(X(:,9)/sum(X(:,9)))*1;     %云服务器1执行时间
        execution_time(1:task_num,2)=(X(:,9)/sum(X(:,9)))*1.3;   %边缘服务器2执行时间
        execution_time(1:task_num,3)=(X(:,9)/sum(X(:,9)))*1.4;     %边缘服务器3执行时间
        execution_time(1:task_num,4)=(X(:,9)/sum(X(:,9)))*2;     %本地终端执行时间
        %execution_time(:,:)=execution_time(:,:).*X(1,10);
        execution_time(:,:)=execution_time(:,:).*sum(X(:,9))./(4*runspped*0.001);
        narvs = size(X(:,9),1)+7;       %目标函数的自变量个数
        task_out=X(:,8);
        task_in=X(1,4);
        task=xlsread("./task.xlsx",i);
        floot_num(i)=sum(X(:,9));
        %% 初始化设置
        if narvs<30
            MaxNum = 300;                          % 粒子最大迭代次数
        else
            MaxNum=narvs*10;
        end
        
        %% 不卸载LOPSO
        narvs=task_num+7;
        x=zeros(1, narvs);         % 粒子所在的位置
        LO=object_value(x,task,execution_time,task_num,task_out,task_in);
        disp("不卸载策略结果：");LO
        LO_result_data=object_result_data(x,task,execution_time,task_num,task_out,task_in);
        
        %% 基于云服务器的完全卸载（FOCPSO）
        [FOC,FOC_strategy]=FOCPSO(task,execution_time,task_num,task_out,task_in);
        disp("基于云服务器的完全卸载:");FOC
        FOC_result_data=object_result_data(FOC_strategy,task,execution_time,task_num,task_out,task_in);
        
        %% 基于端云的部分卸载（POPSO）
        [PO,PO_strategy]=POPSO(task,execution_time,task_num,task_out,task_in,LO,MaxNum);
        disp("基于端云的部分卸载:");PO
        PO_result_data=object_result_data(PO_strategy,task,execution_time,task_num,task_out,task_in);
        
        %% 端-云-边多重资源卸载策略（MRPSO）
        [MR,MR_strategy] = MRPSO(task,execution_time,task_num,task_out,task_in,LO,MaxNum);
        disp("端-云-边卸载策略:");MR
        MR_result_data=object_result_data(MR_strategy,task,execution_time,task_num,task_out,task_in);
        
        %% 结果存储
        result(i,:)=[LO FOC PO MR];
        purchase_cost(i,:)=[LO_result_data(1) FOC_result_data(1) PO_result_data(1) MR_result_data(1)];
        completion_time(i,:)=[LO_result_data(2) FOC_result_data(2) PO_result_data(2) MR_result_data(2)];
        Power_Cost(i,:)=[LO_result_data(3) FOC_result_data(3) PO_result_data(3) MR_result_data(3)];
        
        %% 卸载方案存储
        lables=["LOPSO";"FOCPSO";"POPSO";"MRPSO"];
        strategy(1:4,:)=[zeros(1, narvs);FOC_strategy;PO_strategy;MR_strategy];
        strategy=[lables,strategy];
        strategy_name=lab(i);
        xlswrite('./'+file_name+'/'+strategy_name+'.xls',strategy);
        clear strategy;
    end
    
    %% 适应度值对比图
    figure();
    b=bar(result);
    grid on;
    xlabel('DNNs')
    legend('LOPSO','FOCPSO','POPSO','MRPSO')
    set(gca,'XTickLabel',{'vgg11','vgg13','vgg16','vgg19','googlenet','darknet53','fuse'})
    title("适应度值对比图");
    
    %% 云配置价格、执行时间、能耗对比图
    figure();
    b=bar(purchase_cost);
    grid on;
    xlabel('DNNs')
    legend('LOPSO','FOCPSO','POPSO','MRPSO')
    set(gca,'XTickLabel',{'vgg11','vgg13','vgg16','vgg19','googlenet','darknet53','fuse'})
    title("云配置价格对比图");
    
    figure();
    b=bar(completion_time);
    grid on;
    xlabel('DNNs')
    legend('LOPSO','FOCPSO','POPSO','MRPSO')
    set(gca,'XTickLabel',{'vgg11','vgg13','vgg16','vgg19','googlenet','darknet53','fuse'})
    title("执行时间对比图");
    
    figure();
    b=bar(Power_Cost);
    grid on;
    xlabel('DNNs')
    legend('LOPSO','FOCPSO','POPSO','MRPSO')
    set(gca,'XTickLabel',{'vgg11','vgg13','vgg16','vgg19','googlenet','darknet53','fuse'})
    title("能耗对比图");
    
    
    figure();
    b=bar(floot_num);
    grid on;
    xlabel('DNNs')
    set(gca,'XTickLabel',{'vgg11','vgg13','vgg16','vgg19','googlenet','darknet53','fuse'})
    title("浮点运算次数");
    
    
    %% 数据存储
    
    lables1=[" ";"vgg11";"vgg13";"vgg16";"vgg19";"googlenet";"darknet53"];
    lables2=["LOPSO","FOCPSO","POPSO","MRPSO"];
    
    completion_time=[lables2;completion_time];
    completion_time=[lables1,completion_time];
    xlswrite('./'+file_name+'/completion_time.xls',completion_time);
    
    purchase_cost=[lables2;purchase_cost];
    purchase_cost=[lables1,purchase_cost];
    xlswrite('./'+file_name+'/purchase_cost.xls',purchase_cost);
    
    Power_Cost=[lables2;Power_Cost];
    Power_Cost=[lables1,Power_Cost];
    xlswrite('./'+file_name+'/Power_Cost.xls',Power_Cost);
    
    result=[lables2;result];
    result=[lables1,result];
    xlswrite('./'+file_name+'/result.xls',result);
    
    %% 清空环境
    clc
    clear
    close all
end

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

🌈4 Matlab代码、数据文档讲解下载

 资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取