👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
💥1 概述
车间调度在制造业和生产系统中起着举足轻重的作用,其根本目的是合理分配有限资源,实现
生产效益最大化。柔性作业车间调度问题( Flexible job-shop scheduling problem,FJSP) 作为传统的作业车间调度问题( Job-shop scheduling problem, JSP) 的扩展,允许工序在其可加工机器集中选择不同的机器进行加工,提高了加工的灵活性,更符合企业实际的生产状况。因此,研究 FJSP 对于解决车间实际问题具有重要意义。近年来,FJSP 受到了广泛研究,越来越多的
智能优化算法被用于求解 FJSP。张晓星等考虑到混合蛙跳算法易于陷入局部最优的问题,引
入局部更新策略进行优化,提出改进的混合蛙跳算法求解 FJSP; Nouiri 等提出一种分布式粒子
群算法并应用于 FJSP; 王雷等提出一种改进的免疫克隆选择算法求解 FJSP,利用自适应变异算
子提高全局最优解的质量; 姜天华引入变邻域搜索并结合遗传算子,提出一种混合灰狼优化算
法求解 FJSP。
车间调度FJSP:基于全球邻域和爬山优化算法的模糊柔性车间调度问题研究
一、研究背景与意义
柔性车间调度问题(Flexible Job Shop Scheduling Problem, FJSP)是传统车间调度问题(Job Shop Scheduling Problem, JSP)的扩展,允许工序在多台机器上加工,提高了调度的灵活性,更符合实际生产需求。然而,实际生产环境中存在诸多不确定性因素,如机器故障、工序时间波动等,导致传统精确调度方法难以适用。模糊柔性车间调度问题(Fuzzy Flexible Job Shop Scheduling Problem, FFJSP)进一步引入了模糊集理论,以处理工序时间的不确定性,使得调度问题更加复杂和贴近实际。
研究FFJSP对于提高生产效率、降低生产成本、缩短交货周期具有重要意义。基于全球邻域和爬山优化算法的混合策略,结合了全局搜索和局部搜索的优势,能够在较大范围内寻找潜在的最优解,并通过爬山策略逐步逼近全局最优解,为解决FFJSP提供了新的思路和方法。
二、问题建模
-
模糊工序时间表示:
- 采用三角模糊数(a, b, c)表示工序时间,其中a表示最小可能时间,b表示最可能时间,c表示最大可能时间。
- 利用α-cut方法将三角模糊数转换为清晰的时间区间,便于计算和比较。
-
数学模型构建:
- 目标函数:以最小化最大完工时间(Makespan)为目标,即所有工序中完成时间最晚的工序的完成时间。
- 约束条件:
- 每个工序只能在一台机器上加工。
- 工序的加工顺序约束,即同一工件的前一道工序完成后才能开始下一道工序。
- 机器上的工序加工顺序约束,即同一机器上相邻加工的工序之间需满足一定的顺序关系。
三、算法设计
-
全球邻域搜索策略:
- 初始解生成:随机生成一组初始解,每个解代表一个可能的调度方案。
- 邻域搜索:定义多种邻域结构,如交换邻域、插入邻域、逆转邻域等。通过对当前解进行邻域结构内的操作,产生新的解。
- 选择操作:根据适应度函数评估邻域解的质量,选择较优的解进入下一代。
-
爬山优化算法:
- 局部搜索:从当前解出发,不断地寻找更优的邻域解,直到找到局部最优解为止。
- 步长调整:根据搜索过程中的反馈信息,动态调整爬山算法的步长,以提高搜索效率。
- 终止条件:当达到最大迭代次数或无法找到更优的邻域解时,终止爬山算法。
-
混合算法流程:
- 初始化:生成初始种群,设置算法参数。
- 全球邻域搜索:在解空间中进行大范围的探索,寻找有希望的区域。
- 爬山优化:在有希望的区域内进行精细的搜索,以找到更好的局部最优解。
- 终止条件:当达到最大迭代次数或满足其他终止条件时,终止算法。
四、实验验证与结果分析
-
实验设置:
- 数据集:采用实际生产数据或标准测试数据集进行验证。
- 参数设置:设置种群规模、最大迭代次数、邻域结构类型等参数。
- 对比算法:选择其他智能优化算法(如遗传算法、模拟退火算法等)作为对比,评估所提算法的性能。
-
实验结果:
- 收敛性分析:通过绘制收敛曲线,观察算法的收敛速度和稳定性。
- 解的质量评估:比较不同算法找到的最优解的质量,评估所提算法的优越性。
- 鲁棒性分析:通过改变参数设置或引入噪声数据,测试算法的鲁棒性。
-
结果分析:
- 算法优势:所提算法结合了全局搜索和局部搜索的优势,能够在较大范围内寻找潜在的最优解,并通过爬山策略逐步逼近全局最优解。实验结果表明,该算法在解决FFJSP方面具有良好的性能和鲁棒性。
- 改进方向:尽管所提算法取得了一定的成果,但仍存在一些不足之处。例如,算法对初始解和参数设置较为敏感;在处理大规模问题时,计算时间可能较长。未来可以进一步研究自适应参数调整策略、多种邻域结构融合方法等,以提高算法的搜索效率和鲁棒性。
📚2 运行结果
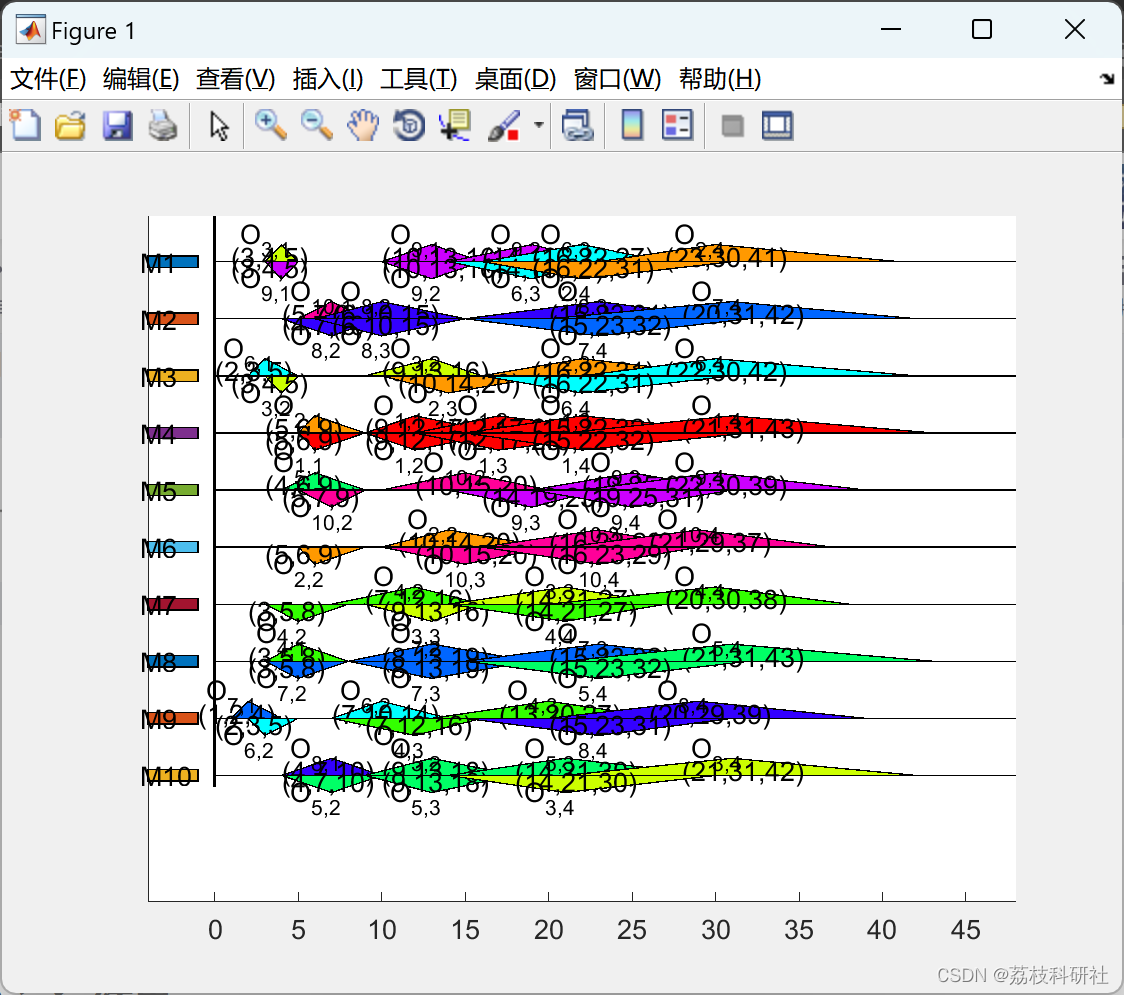
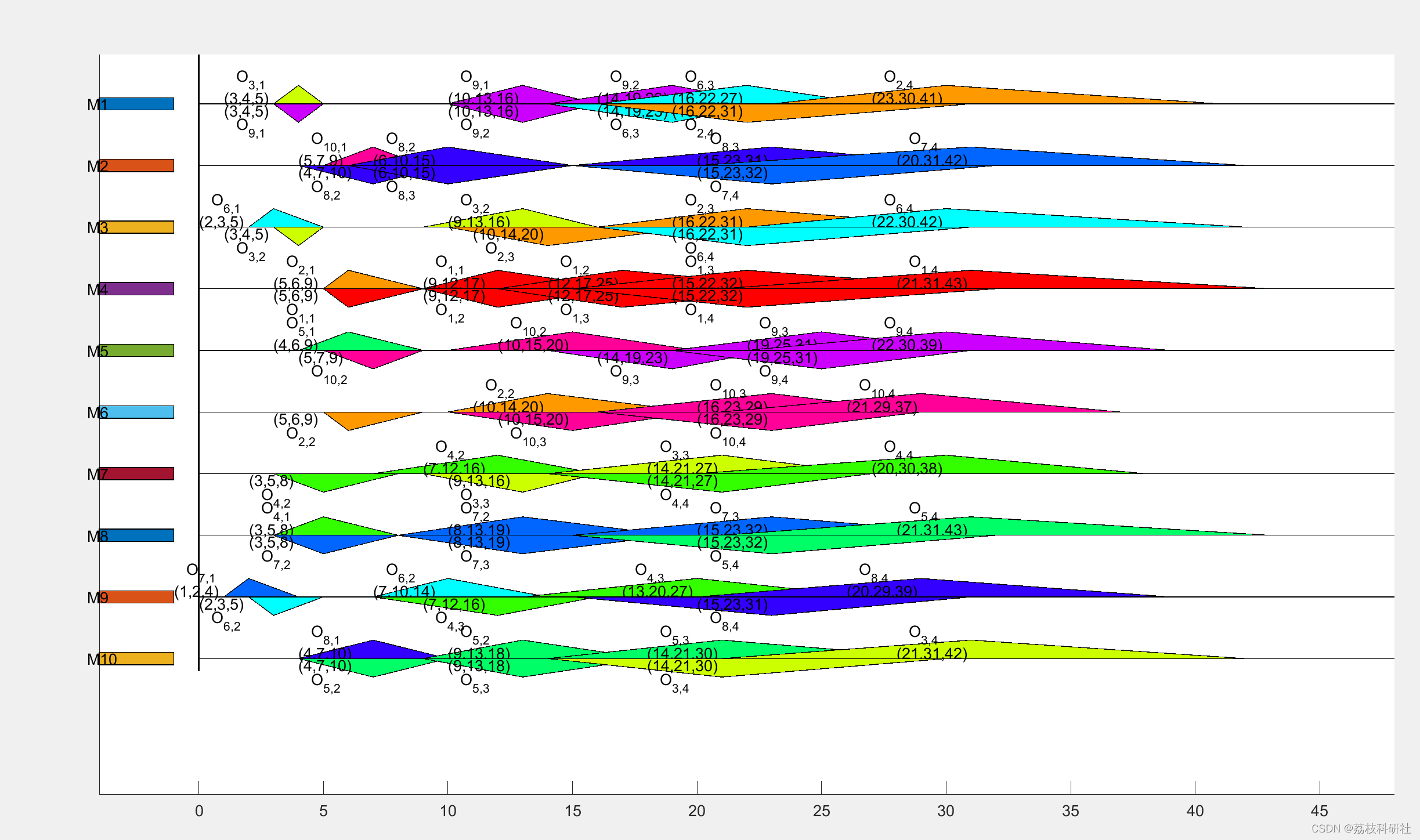
部分代码:
%Smart-cell array
PoblacionSO=zeros(numIndividuos,numOperaciones);
PoblacionSM=zeros(numIndividuos,numOperaciones);
PoblacionMakespan=zeros(numIndividuos,3);
%Jobs table,
%Columns ordered by job and operation (J_11, J_12, ... Jnm-1, Jnm)
%Row order:
%Assigned machine
%Processing position in the assigned machine
%Minimum processing time
%Most probable processing time
%Maximum processing time
%Operation position in SO
%Position of the previous operation in the table
PoblacionTablaTrabajos=zeros(10,numOperaciones,numIndividuos);
%Machine table,
%Columns ordered by machine and operation (M_11, M_12, ... Mmo-1, Jmo)
%Row order:
%Job assigned to the machine
%Operation of the job
%Minimum processing time
%Most probable processing time
%Maximum processing time
%Operation position in SO
PoblacionTablaMaquinas=zeros(9,numOperaciones,numIndividuos);
PoblacionVectorMaquinas=zeros(numIndividuos,numeroMaquinas);
PoblacionVectorOrdenMaq=zeros(numIndividuos,numOperaciones);
PoblacionPosMk=zeros(numIndividuos,1);
PoblacionPosTT=zeros(numIndividuos,numOperaciones);
PoblacionPosTM=zeros(numIndividuos,numOperaciones);
%Random initial population of smart-cells
for i=1:numIndividuos
[PoblacionSO(i,:),PoblacionSM(i,:)] = generarIndividuoAleatorio(numeroMaquinas,numOperaciones,vectorOperaciones,tablaMaquinasFactibles);
end
%Evaluate population
[PoblacionMakespan, PoblacionPosMk, PoblacionTablaTrabajos, PoblacionTablaMaquinas, PoblacionVectorMaquinas, PoblacionVectorOrdenMaq, PoblacionPosTT, PoblacionPosTM] = calificarPoblacion(PoblacionSO, PoblacionSM, PoblacionMakespan, PoblacionPosMk, PoblacionTablaTrabajos, PoblacionTablaMaquinas, PoblacionVectorMaquinas, PoblacionVectorOrdenMaq, PoblacionPosTT, PoblacionPosTM, numeroTrabajos, numeroMaquinas, numOperaciones,numIndividuos,vectorNumOperaciones,vectorInicioOperaciones, tablaTiempos, 1);
%Select the best smart-cell
[mejorSO, mejorSM, mejorMakespan] = mejorIndividuo(PoblacionSO, PoblacionSM, PoblacionMakespan);
%Elitist smart-cells
numIndEl=round(numIndividuos*probElitista);
if mod(numIndividuos-numIndEl,2)==1
numIndEl = numIndEl+1;
end
contIt=1;
contEst=1;
banderaCiclo=1;
%Convergence vector
convergencia=[];
convergencia(contIt,:)=mejorMakespan;
%Optimization loop
while(banderaCiclo)
%Selection
[PoblacionSO, PoblacionSM, PoblacionMakespan,PoblacionPosMk, PoblacionTablaTrabajos, PoblacionTablaMaquinas, PoblacionVectorMaquinas, PoblacionVectorOrdenMaq, PoblacionPosTT, PoblacionPosTM] = seleccion(PoblacionSO, PoblacionSM, PoblacionMakespan, PoblacionPosMk, PoblacionTablaTrabajos, PoblacionTablaMaquinas, PoblacionVectorMaquinas, PoblacionVectorOrdenMaq, PoblacionPosTT, PoblacionPosTM, numIndividuos, numIndEl, 2);
%GN-HC neigborhood
[PoblacionSO, PoblacionSM, PoblacionMakespan,PoblacionPosMk, PoblacionTablaTrabajos, PoblacionTablaMaquinas, PoblacionVectorMaquinas, PoblacionVectorOrdenMaq, PoblacionPosTT, PoblacionPosTM] = aplicacionVecindadGN_HC(PoblacionSO, PoblacionSM, PoblacionMakespan, PoblacionPosMk, PoblacionTablaTrabajos, PoblacionTablaMaquinas, PoblacionVectorMaquinas, PoblacionVectorOrdenMaq, PoblacionPosTT, PoblacionPosTM, tamVecindad, numIndividuos, numeroTrabajos, numeroMaquinas, numOperaciones, vectorInicioOperaciones, tablaTiempos, tablaMaquinasFactibles, vectorNumOperaciones, numIndEl);
%Hill climbing
[PoblacionSO, PoblacionSM, PoblacionMakespan,PoblacionPosMk, PoblacionTablaTrabajos, PoblacionTablaMaquinas, PoblacionVectorMaquinas, PoblacionVectorOrdenMaq, PoblacionPosTT, PoblacionPosTM] = busquedaPoblacionalEscaladaColina(PoblacionSO, PoblacionSM, PoblacionMakespan, PoblacionPosMk, PoblacionTablaTrabajos, PoblacionTablaMaquinas, PoblacionVectorMaquinas, PoblacionVectorOrdenMaq, PoblacionPosTT, PoblacionPosTM, numIndividuos, iteracionesTotalesEscalada, iteracionesReinicioEscalada, numeroTrabajos, numeroMaquinas, numOperaciones, vectorInicioOperaciones, tablaTiempos, tablaMaquinasFactibles, vectorNumOperaciones, numIndEl);
%Select best solution in the iteration
[nuevaMejorSO, nuevaMejorSM, nuevaMejorMakespan] = mejorIndividuo(PoblacionSO, PoblacionSM, PoblacionMakespan);
%If improved, update best solution
[~,pos] = mayor_difuso(mejorMakespan,nuevaMejorMakespan);
if pos==1
suma=sum(mejorMakespan==nuevaMejorMakespan);
if suma<3
mejorSO = nuevaMejorSO;
mejorSM = nuevaMejorSM;
mejorMakespan = nuevaMejorMakespan;
contEst=1;
else
%Increase stagnation
contEst=contEst+1;
end
else
contEst=contEst+1;
end
%Halt condition
if ((contEst>=numEstancamiento) || (contIt>=numGeneraciones))
banderaCiclo=0;
end
%Print best fuzzy makespan
if mod(contIt,20)==0 && bandImp==1
disp(['Iteracion: ' num2str(contIt) ' Makespan: ' num2str(mejorMakespan)])
end
contIt=contIt+1;
%Keep convergence
convergencia(contIt,:)=mejorMakespan;
end
end
%Random smart-cell
function [so,sm] = generarIndividuoAleatorio(numeroMaquinas,numOperaciones,vectorOperaciones,tablaMaquinasFactibles)
indices=randperm(numOperaciones);
so=vectorOperaciones(indices);
lista_maquinas = 1:numeroMaquinas;
sm=zeros(1,numOperaciones);
for i=1:numOperaciones
maquinas=tablaMaquinasFactibles(i,:);
factibles = lista_maquinas(logical(maquinas));
numMaquinas=length(factibles);
indMaquina=randi([1 numMaquinas]);
maquina=factibles(indMaquina);
sm(i)=maquina;
end
end
%Evaluate population
function [PobMk, PobPMk, PobTT, PobTM, PobVM, PobVOM, PobPTT, PobPTM] = calificarPoblacion(PobSO, PobSM, PobMk, PobPMk, PobTT, PobTM, PobVM, PobVOM, PobPTT, PobPTM, numeroTrabajos, numeroMaquinas, numOperaciones,numIndividuos,vectorNumOperaciones,vectorInicioOperaciones, tablaTiempos, inicio)
for i=inicio:numIndividuos
[PobMk(i,:), PobPMk(i), PobTT(:,:,i), PobTM(:,:,i), PobVM(i,:),PobVOM(i,:), PobPTT(i,:), PobPTM(i,:)] = calcularMakespanActivoTablas(PobSO(i,:),PobSM(i,:),numeroTrabajos, numeroMaquinas, numOperaciones, vectorNumOperaciones,vectorInicioOperaciones, tablaTiempos, PobTT(:,:,i), PobTM(:,:,i), PobVM(i,:), PobVOM(i,:), PobPTT(i,:), PobPTM(i,:));
end
end
%Calculate fuzzy makespan
function [makespan,posmk,TablaTrabajos,TablaMaquinas,vectorMaquinas,vectorOrdenMaq,posTT,posTM] = calcularMakespanActivoTablas(so,sm,numeroTrabajos, numeroMaquinas, numOperaciones, vectorNumOperaciones,vectorInicioOperaciones, tablaTiempos, TablaTrabajos, TablaMaquinas, vectorMaquinas, vectorOrdenMaq, posTT, posTM)
makespan = zeros(1,3);
posmk = 0;
[~,pos] = mayor_difuso(mejorMk,z2);
if pos==1
mejorMk = PobMk(i,:);
mejorSO = PobSO(i,:);
mejorSM = PobSM(i,:);
indice = i;
end
end
end
%Selection by elitism and tournement
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Juan Carlos Seck Tuoh Mora Nayeli Jazmin Escamilla Serna,A global neighborhood with hill climbing algorithm for fuzzy flexible job shop scheduling problem.
[2]范书宁,余开朝,万雨松.改进MOEA/D算法求解多目标模糊柔性车间调度问题[J].计算机应用研究,2023,40(01):192-197.DOI:10.19734/j.issn.1001-3695.2022.06.0290.
[3]李旻运. 基于改进的NSGA2算法的多目标柔性车间调度问题的研究及应用[D].湖州师范学院,2022.DOI:10.27946/d.cnki.ghzsf.2022.000051.
[4]蔡敏,王艳,纪志成.混合粒子群优化算法求解模糊柔性作业车间调度问题[J].南京理工大学学报,2021,45(03):352-360.DOI:10.14177/j.cnki.32-1397n.2021.45.03.014.
 基于GN-HC算法的FFJSP研究
基于GN-HC算法的FFJSP研究




















 1319
1319

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








