一、背景
由于一些数据集扫描出来的结果并不清楚,3d建模后在某些位置可能出现凹陷,因此对应的皮肤表皮轮廓也会有相应的凹陷。任务便是想出一些方式“修复”这些凹陷,使表皮更加光滑。
二、尝试
方式一:
mt介绍完这个任务时说了他们以前的尝试方式,主要是通过对轴冠矢三面进行处理来减小凹陷的影响,还说了一种思路是直接将原图3d建模,在3d建模时考虑光照的一些影响可能会对凹陷部位进行修复。即最终得出的3d模型中凹陷会修复,之后对整个3d模型提取表面,即3d皮肤模型。他们说这种思路以前还未尝试,所以我先尝试的这一种方式。
思路大概是先根据源数据形成三维mask,然后提取mesh,检查mesh的表面,我一开始以为水密性watertight是会检测表面是否有凹陷。如果有的话就填充。但是我对水密性这个概念有误解。满足水密性是说mesh表面完全封闭。3d建模时凹陷部位并不是一个“孔洞”,他只是凹下去了,并不是缺失,所以表面仍然是封闭的。
根据水密性可以填充“孔洞”,如下图所示:
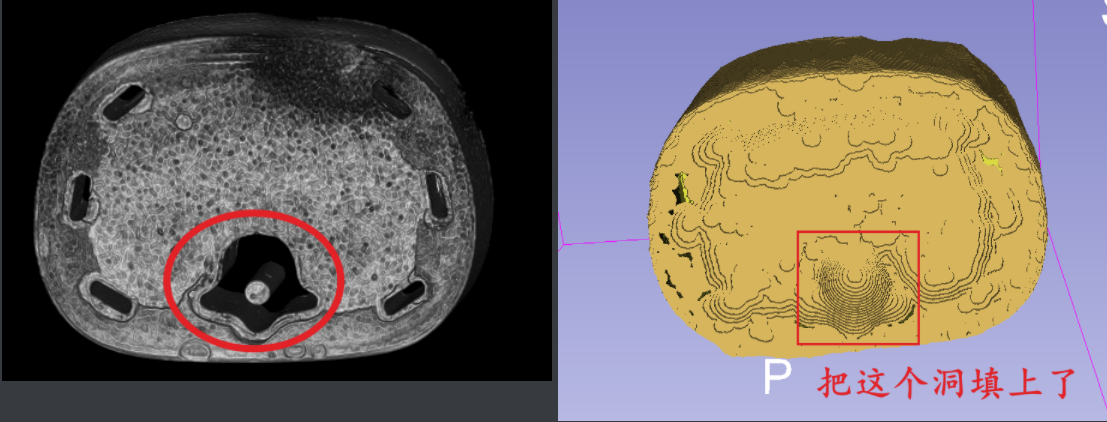
上图中3d建模后红色框原本是空的,不满足水密性,检测出来之后填充就会一定程度上填充这个洞。这才是水密性的用途。
对于这个思路由于3d建模过程都是gpt写的代码,我不明白其中原理,无法调试,所以就放弃了。
方式二:
之后还是想着从轴面轮廓开始做,因为其中的操作我明白具体是什么。首先是对原始影像进行预处理,起码得出比较清晰的轮廓。当时想,对于轮廓严重缺失的,直接舍弃,例如下面的轮廓:
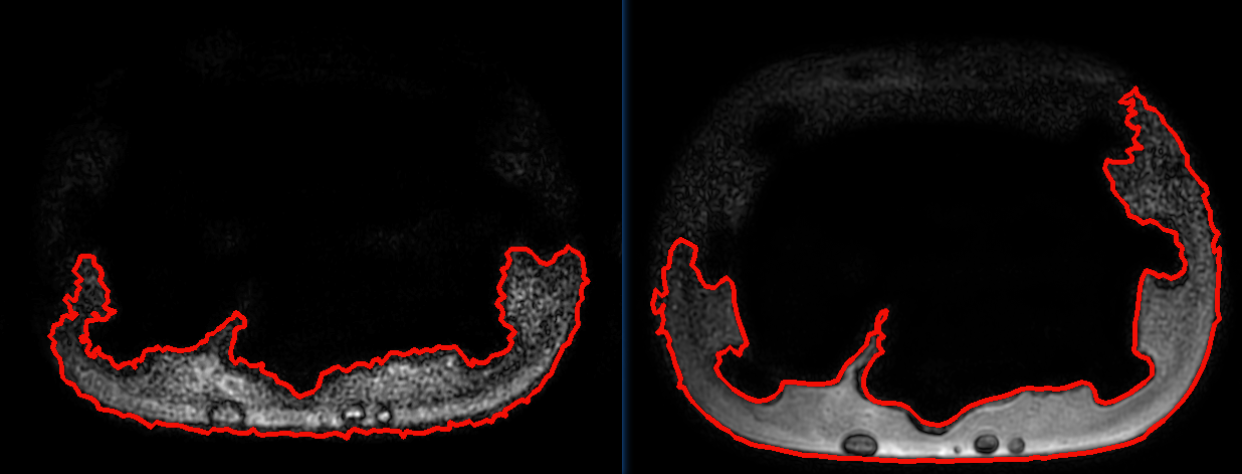
对有"轻微凹陷"的轮廓进行修改,像下面这种:
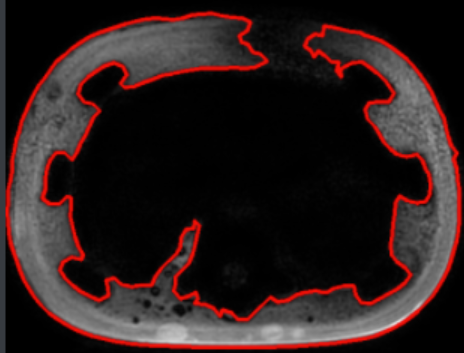
整体思路:
-
预处理图像
-
通过findcontours函数找出轮廓
-
找到凹陷的拐点,然后通过曲线拟合修补
预处理阶段:
-
首先对所有影像归一化
-
假如当前影像是第i张,我会将各自归一化之后的i-1,i,i+1这三张影像相加,作为增强
-
之后进行闭运算,采用的核大小为(7,7)
-
模糊处理,核大小为(5,5)
-
使用Otsu阈值分割,第一次运行Otsu会得出一个阈值ret,之后还会在根据阈值ret-20在进行简单分割。mt当时说过对于mr影像这样做得到的分割效果更好,我经过测试发现确实如此。
-
使用findcontours函数寻找轮廓,最大的轮廓就是我们要处理的。
以上是预处理的大致步骤,记得当时寻找轮廓时遇到一个问题,
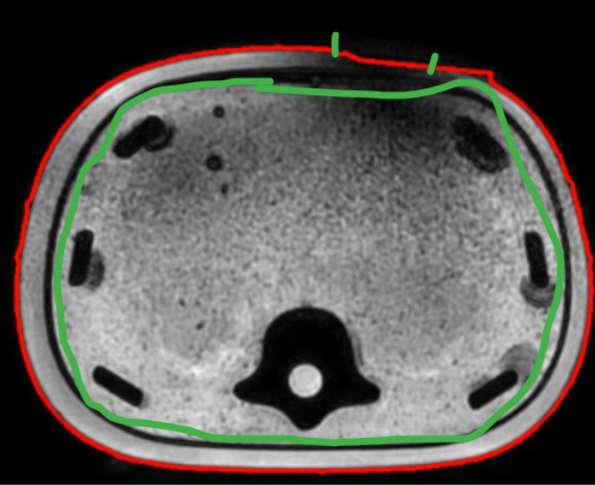
比如上图,外面的红色轮廓在绿色竖线部分是有缺口的,所以外面的轮廓就不完整,恰好里面绿色轮廓完整,而且和外面”不粘连“,所以扫描出来的结果最大轮廓是里面的轮廓。如下图所示:
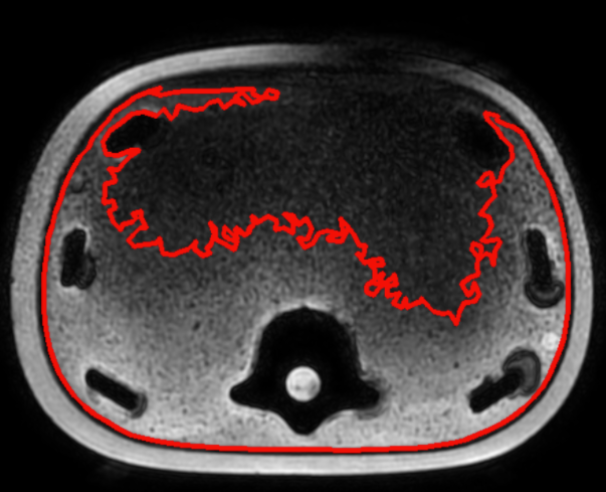
这里当时是通过在模糊处理之前加一个(7*7)的闭运算解决的。通过这个闭运算,内外部分会粘连到一起,不会出现完全分隔开的情况。根据开闭运算的原理,闭运算确实能填补内部的一些缝隙,而开运算则能消除内部的一些噪点,小黑洞,如下面两幅图:
闭运算:
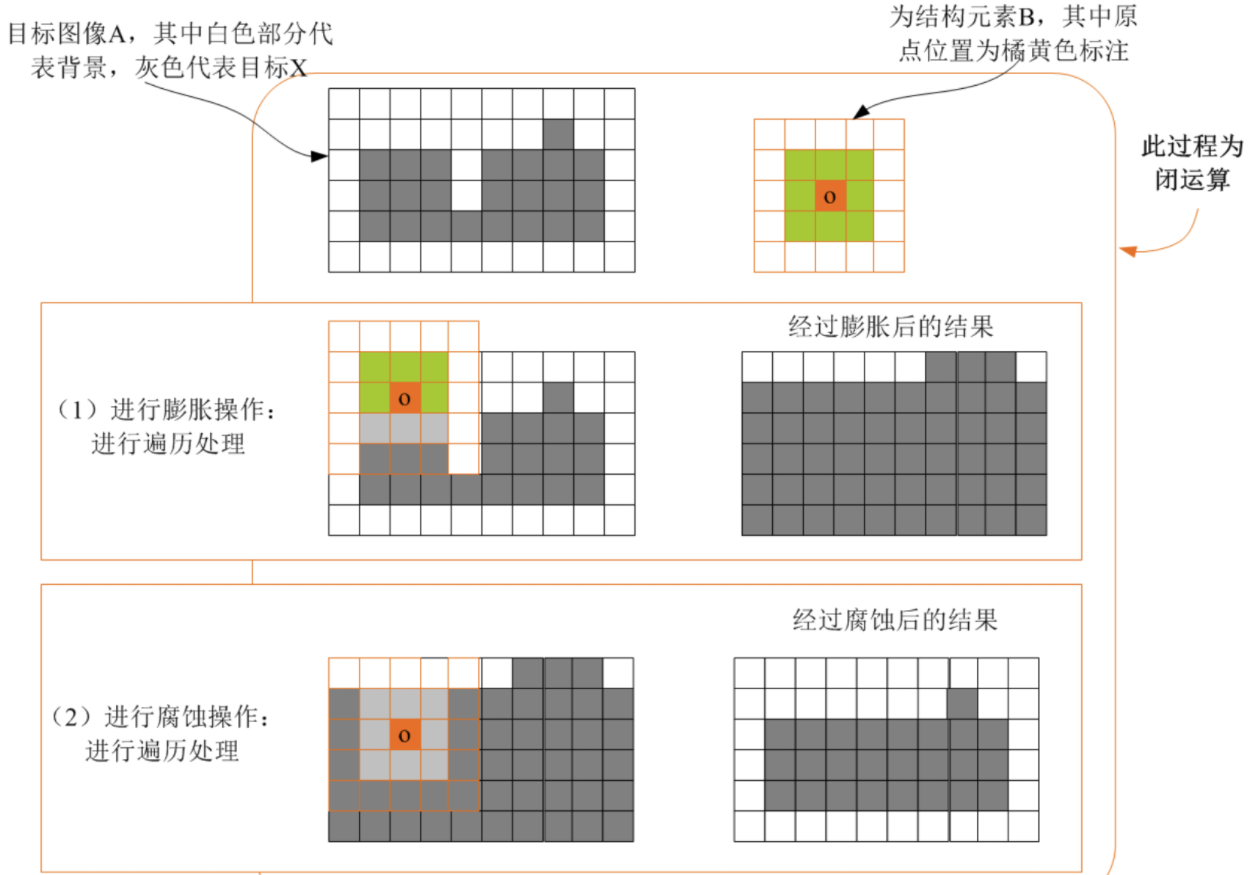
开运算:
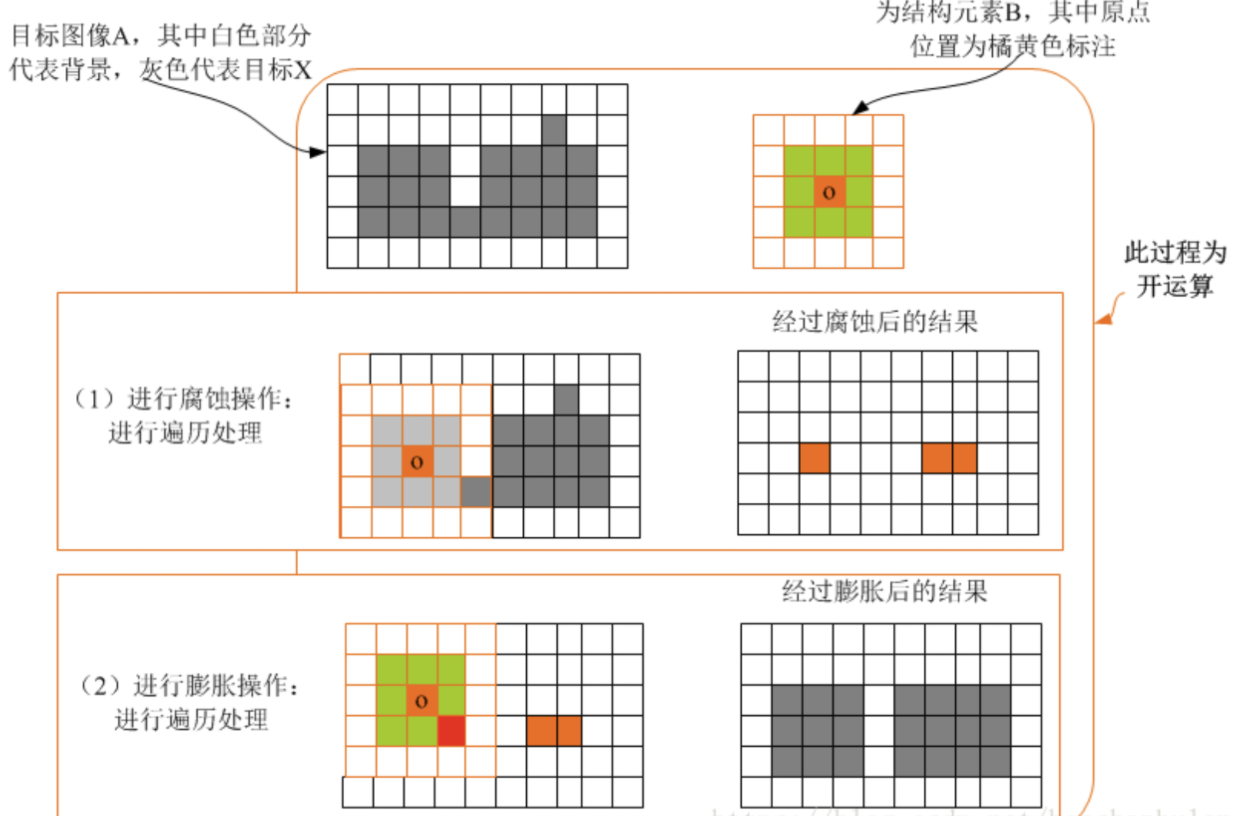
寻找凹陷拐点:
这是主线任务,也是难点。
方式一:
对于凹陷的拐点,我首先尝试用一个滑窗取扫描轮廓,滑窗中三个点,根据其形成的两条直线夹角进行判断
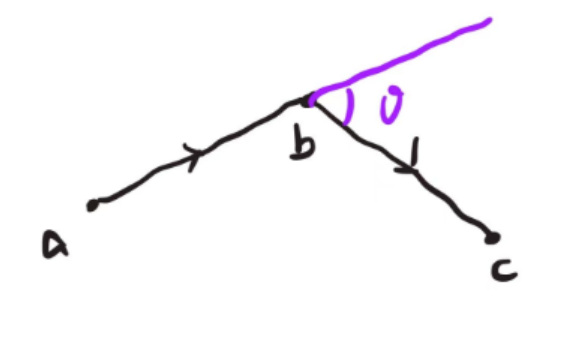
我想着身体部分是平滑的,如果这两条线段形成的夹角太大,说明就是凹陷。这种方式效果不好,原因是三个点太少,误差太多。
然后增加滑窗内的点,增加到七个:
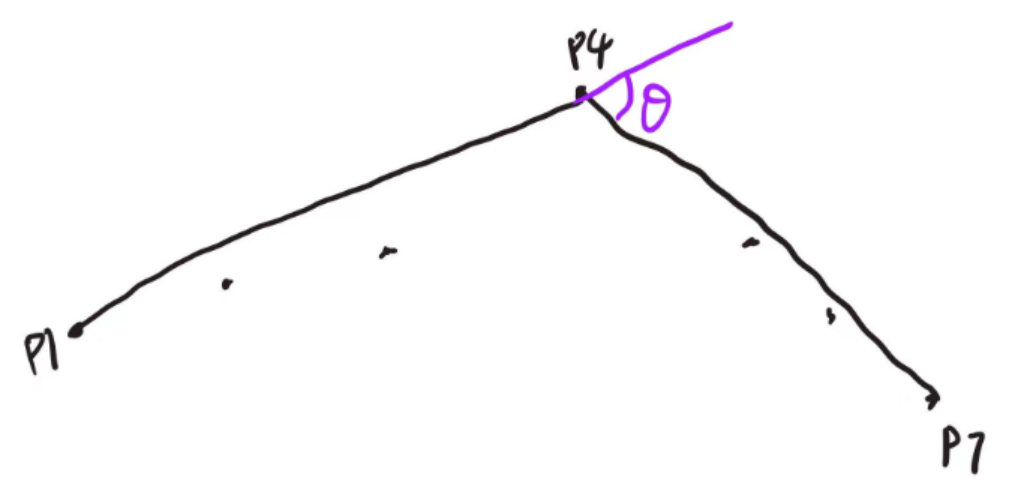
此时效果比上面的好多了,但是,这种方法本身局限性太大,准确度也不能达到很高。
还有一种思路:即统计滑窗内七个点形成的线段的累计夹角,将夹角和与一个阈值做判断,但是如果遇到下面这种情况,就不可以:

如图中绿色框,绿色点。显然这是一个拐角,但是这个拐角的累加和并不会太高。在这个滑窗内只有一个夹角会很大。其余都很平滑。
以上是自己当时想得判断思路。
之后和mt交流,提供了两种思路:(这两个思路是将知道凹陷位置后如何对凹陷进行处理的,并不是寻找拐点的)
思路一:

比如我们知道图中黄色框位置有一个凹陷存在,我们单独对这个滑窗内的图像进行Otsu处理,考虑到一开始由于凹陷部位的像素在图像中相对较低,所以Otsu时分割不明显,如果我们只聚焦于当前位置,进行Otsu阈值分割,或许可以恢复凹陷部分。
但是,存在下面这样的情况:

如图,红色框内属于边缘部分的伪影,绿色框是正常凹陷位置部分,但伪影的像素值原本大于正常凹陷中的部分,所以在Otsu阈值分割时,伪影也会被规划到前景中,所以处理后会出现下面这种情况:
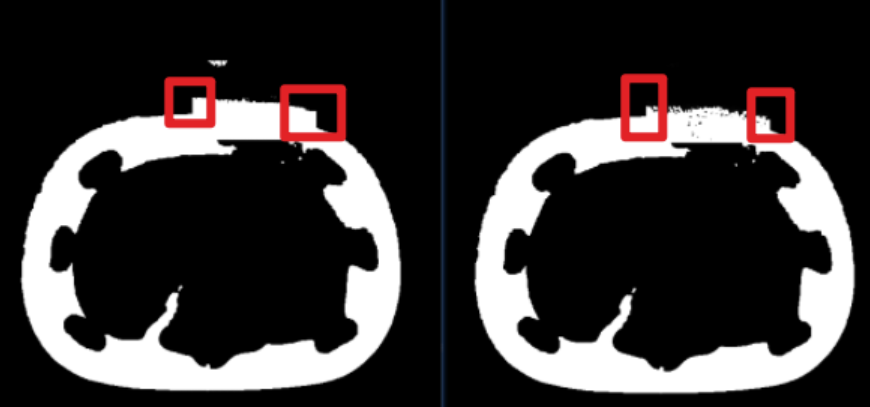
处理后凹陷部分会有凸出,这个也不好处理。
思路二:

比如当前层凹陷区域,在滑窗内,比如上图6滑窗,我们寻找一个”没有凹陷的影像“作为对比,也用一个滑窗卡住相同位置,比如上左图5,我们在5中计算出非零像素的占比percentile,然后在6中调试一个阈值thresh,用这个阈值分割后非零像素占比达到percentile即可。以这种方式恢复凹陷区域。
但是,这种方式同样会出现思路一中的问题。故放弃
最终方式
mt提到一种通过相邻层轮廓对比进行凹陷判断的方式,即用一个”完好“的轮廓作为参照,同时扫描当前轮廓和参考轮廓。思考之后我认为这种方式不错,简洁而全面。
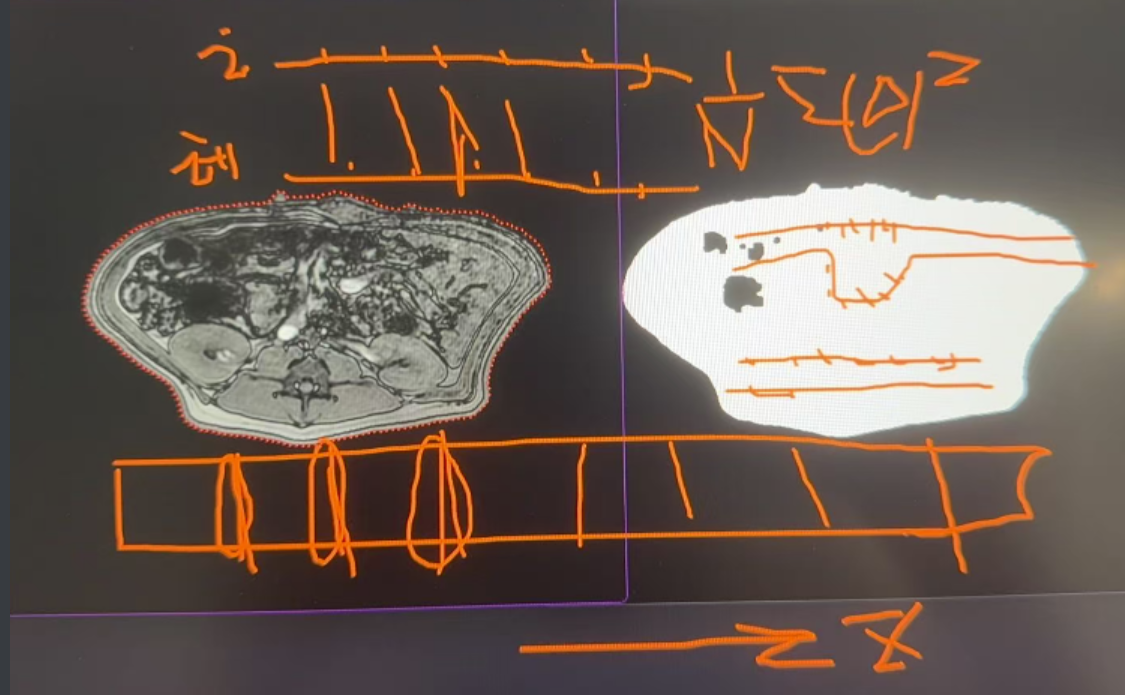
但是这种方式关键在于如何扫描两个轮廓。
因为通过findcontours扫出来之后每个影像的轮廓点数不同,不能做到”相同下标的点对应两个轮廓中的相同位置“,即使你把他们都采样到相同点数,用滑窗扫描的方式也无法达到这个要求,所以不能用滑窗的方式。
之前mt提到他寻找拐点是先找出质心,求圆上点到质心的极角,对于轮廓上的点按照顺时针扫描,正常来说极角递增,如果某位置出现反向,即递减,那么就判断为凹陷的一个拐点。
基于这种方式,以同样的扫描方式,同时对两个轮廓进行同步扫描,一个是参考轮廓,它是“完好没有凹陷”的轮廓;一个是当前要处理的轮廓,即判断有没有凹陷。
首先在图中使用极坐标系,质心为原点,如下图:
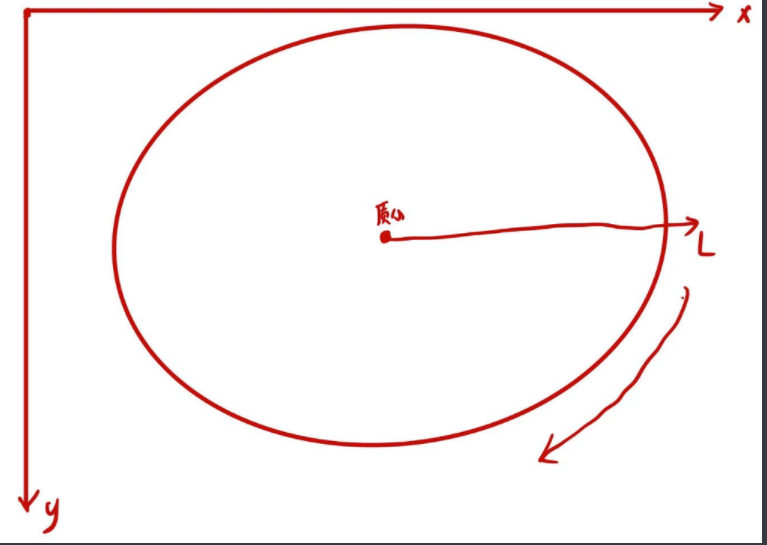
因轮廓是一周,即一个圆,在轮廓上采样180个点,即相邻点之间2°。
然后计算轮廓上点到质心半径,那么对于轮廓上每一个点都可以用(r,θ)来表示。
我们首先要对通过findcontours得到的轮廓进行采样,得到一周的点.即180个.
对原轮廓以这种方式进行轮廓采样:
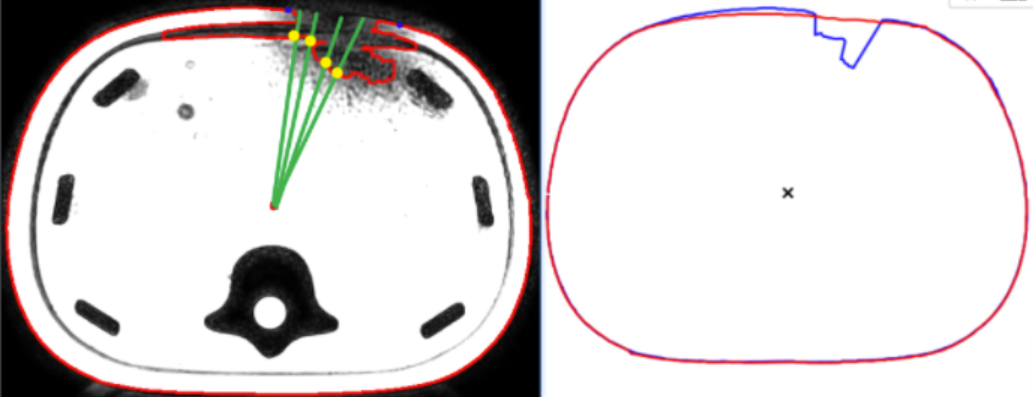
比如上左图中轮廓采样后就是右图中蓝色轮廓。
如果凹陷部位完全缺失,相应角度上的点我们取质心作为轮廓点。
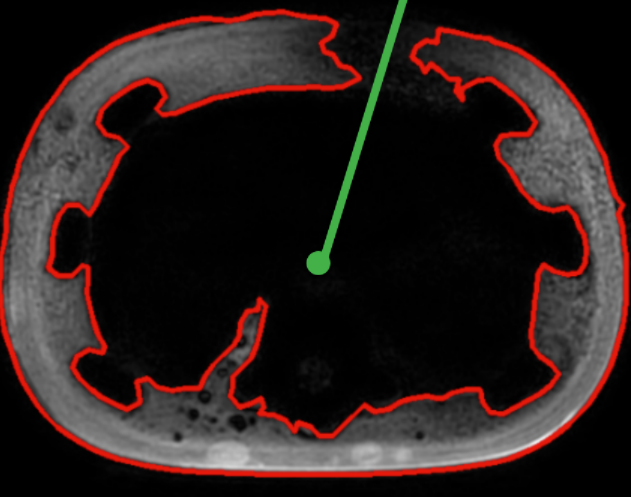
比如上图中在这个角度,轮廓上没有对应的点,此时设置轮廓点为质心。,取轮廓之后结果如下图。
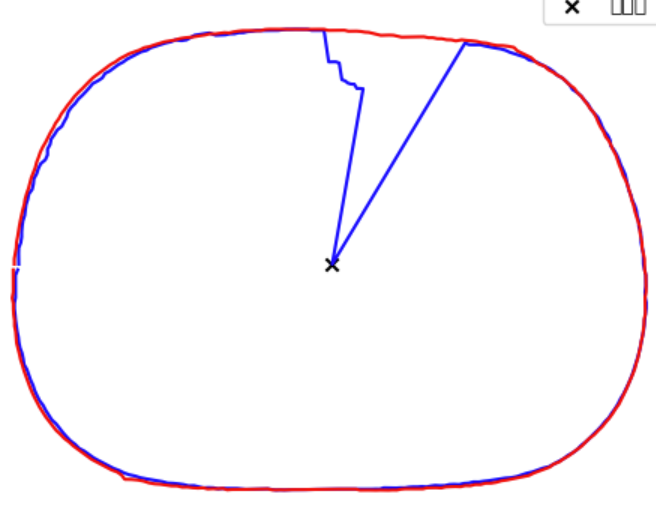
对于下图中某一个角度上有内外两层轮廓,正常的是外层轮廓,所以我们取半径最大的点作为轮廓点.因此,对于外凸的缺口,我们就不能处理,在那种缺口中,某一个角度对应多层轮廓,应该取半径较小的.
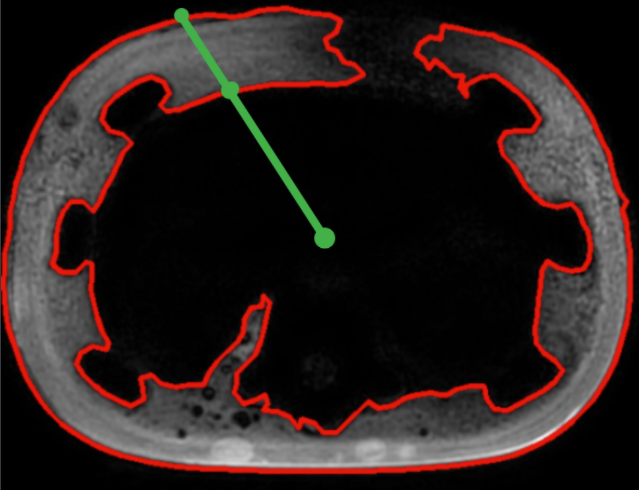
注意:对于一个数据集,质心我取中间影像的质心(默认中间影像是“完好”的),所有影像公用这一个质心。
之后就是扫描确定凹陷位置:
对当前轮廓(图中蓝色轮廓)和参考轮廓(图中红色轮廓)进行同步扫描。对于两个轮廓上相同θ的点的半径r,如果半径差大于设定的阈值,就认为是凹陷,如下图:
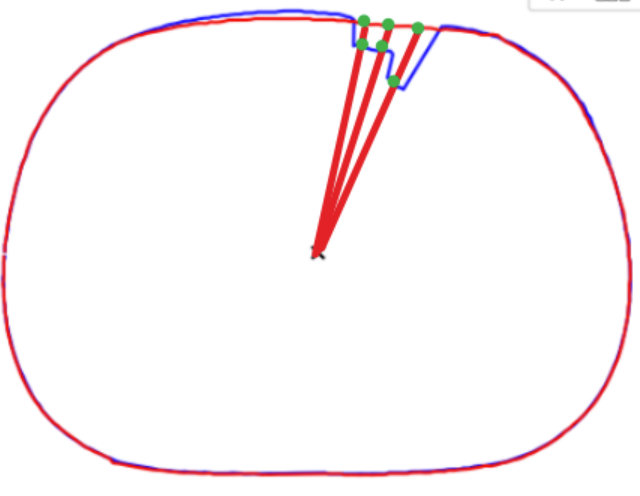
通过以上方式,我们能找到连续的凹陷点,两端就是凹陷的拐点,在两个拐点之间进行曲线拟合即可。
缺陷:
-
不能处理外凸型缺口
-
此方法前提是整个数据集中有"完好没有凹陷"的参考轮廓,如果不存在参考轮廓,则不能奏效
以上就是主要思路
接下来是写代码过程中遇到的问题
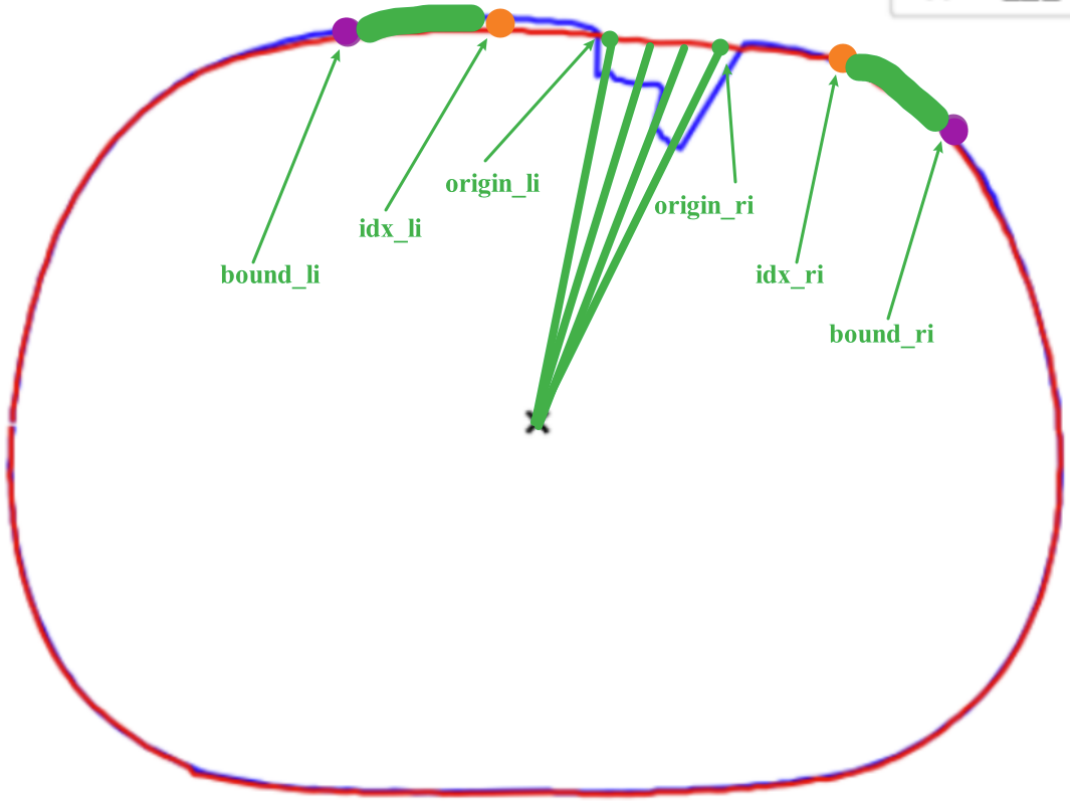
如上图所示:通过半径差能确定凹陷的边界origin_li,origin_ri.需要确保拟合曲线用得点在凹陷外,所以我先各自偏移十个点得到idx_li,idx_ri.之后再偏移十个点得到bound_li,bound_ri.用[bound_li:idx_li],[idx_ri:bound_ri]上的点进行B样条拟合.
一周对应的角度记录在theta_grid中:
N = 180 # 圆周取180个点 theta_grid = np.linspace(-np.pi, np.pi, N, endpoint=False) # 一周180个点
圆周上180个点,通过:
theta = np.arctan2(cnt[:, 1], cnt[:, 0]) # cnt记录的是圆周上点的坐标 # 将 theta 映射回 [-π, π) theta = (theta + np.pi) % (2 * np.pi) - np.pi # 分配到角度 bin bin_indices = np.digitize(theta, theta_grid) - 1
np.digitize()函数要求theta_grid单调,这里以后会遇到一个问题,后面再说。
通过下面的函数计算每个点的半径,(这里计算的是点到原点(0,0)的距离,这也是为什么对所有点先减去质心centroid
r = np.linalg.norm(cnt, axis=1)
所以我们有如下四个数组
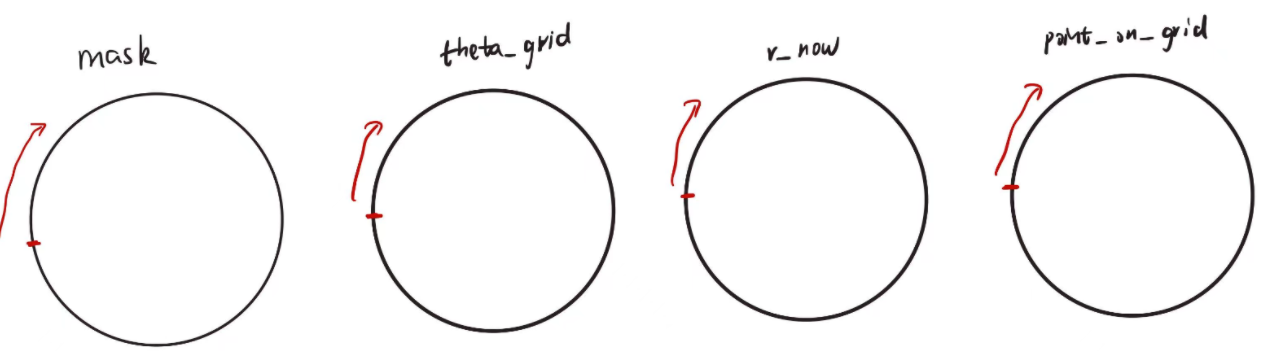
mask # mask = diff_r > thresh 记录半径差是否大于阈值,为true表示凹陷部位 theta_grid # 记录一周的角度 r_now # 记录当前层轮廓上各个角度对应的半径 point_on_grid #记录当前层轮廓上的点
都是顺时针方向存储,从红点开始。
因为我们要取[bound_li:idx_li],[idx_ri:bound_ri]这部分的点,而一开始只知道origin_li,origin_ri。如果凹陷在下图这个位置:
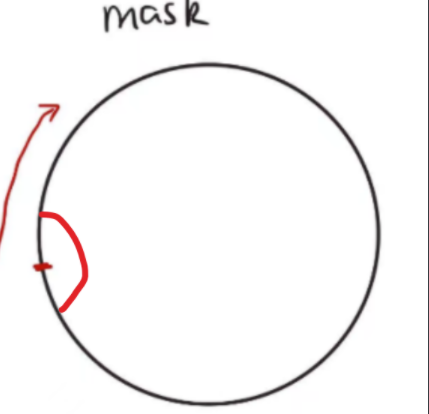
取拟合需要的点时就要考虑数组起点在凹陷中的位置,一共有六种情况:
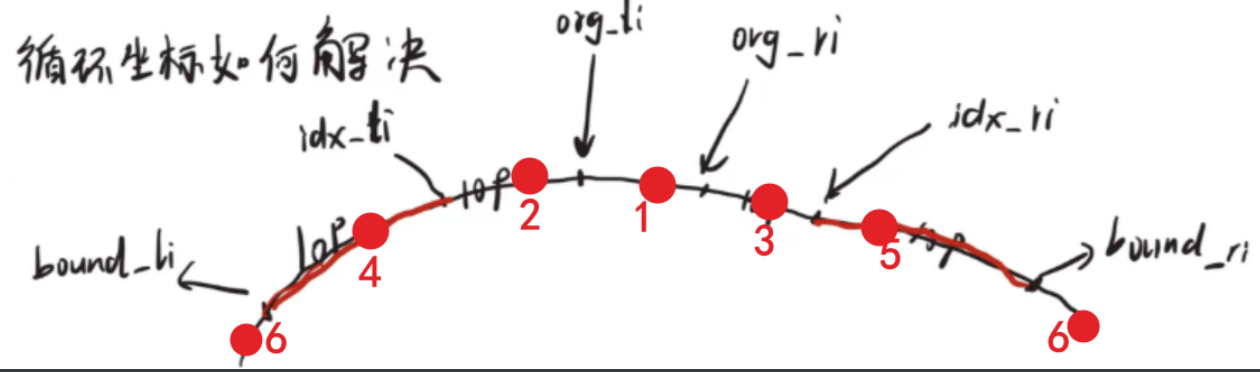
如果用if-else写,下标范围极容易出错。
想到的解决方法是:
mask、theta_grid、r_now、points_on_grid这四个数组下标都是一一对应的。
将每个数组重复三次,以mask数组为例:

原先每个数组都是180个点。我们从在[180:360]范围内进行扫描,如果连续20个点mask都是false,那么用这段的右端点作为start,在区间[start:start+180]上进行操作。这样就会避免出现凹陷在数组0位置处。这里为什么要连续20个点呢?因为[bound_li:origin_li], [origin_ri:bound_ri]各自最多只有20个点,只会有一端出现在数组0附近,所以只需要20个点。
代码中是这样进行实现的。
上面的思路等效于下面的:

这次不扩容,只是将原来数组前面的一部分移动到数组的尾部。
从数组开头进行扫描,如果找到一个大小为40的连续区间,用区间中间作为新数组的头。
这里为什么是40,而不是20?因为如果是20,新数组头部和尾部我们最多保证10个点是正常点,如果我们在index=11处找到凹陷点坐标origin_li,那么拟合需要的点[bound_li:idx_li]就会是负的,虽然可以通过取模进行处理,但是很麻烦。
如果是40,那么新数组头部尾部最多都可以保证20个正常点,那么[bound_li:idx_li]就不会越界。
以上是编码遇到的第一个问题。
另一个问题是关于theta_grid的。
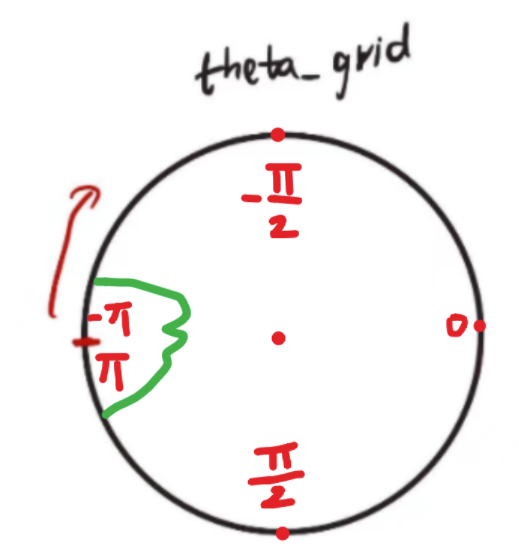
首先极坐标中点的角度划分如上图所示。
如果凹陷跨越theta_grid的头部和尾部,如上图绿色部分。那么角度范围可能是[\frac{3\pi}{4}:\frac{-3\pi}{4}],我们通过曲线拟合在[idx_li:idx_ri]上拟合出对应的点,将这些点分配到[\frac{3\pi}{4}:\frac{-3\pi}{4}],代码如下:
# 计算出点对应的角度 theta = np.arctan2(cnt[:, 1], cnt[:, 0]) # 将 theta 映射回 [-π, π) theta = (theta + np.pi) % (2 * np.pi) - np.pi # 分配到角度 bin bin_indices = np.digitize(theta, theta_grid) - 1
其中np.digitize()函数要求theta_grid必须是单调的。对于这部分采取的方式是分两步进行,将角度分为[\frac{3\pi}{4}:\pi]、[-\pi:\frac{-3\pi}{4}],也将生成的点分成对应两段进行分配。
以上shi方案一的思路
后来又忽然想到,我采用的是参考轮廓和当前轮廓进行对比,如果发现当前轮廓有凹陷,就通过当前轮廓上正常的点进行拟合曲线,来修补凹陷位置。
将参考轮廓和当前轮廓对比,本质上不是说明参考轮廓是当前轮廓的“目标形态”吗,那我在找到凹陷区域后,为什么不直接用参考轮廓上对应的点直接来替代当前轮廓上凹陷位置的点呢?
基于此思路,有了方案二:
方案二是在当前轮廓检测到凹陷后,对于要修补的区域[idx_li:idx_ri],直接用参考轮廓对应区域的点替代。 认为这种方式比方案一实现简单,效果也好点,能修补所有影像,因为即使很差的影像,我们也是用参考轮廓替代当前 影像的轮廓 程序中完好轮廓默认采用的是数据集最中间的一层 缺点: 1、如果一个数据集中没有一张完好的轮廓,则不能用这种方法 优点: 1、只要数据集中有完美轮廓,向内凹陷,向外凹陷都能够处理 2、速度快,对同一个数据集,方案一耗时约4.3s 而方案二耗时2.8s
但实验中发现该方案有一个问题,它会抑制原本正常的“扩大”,”缩小“。如下图:
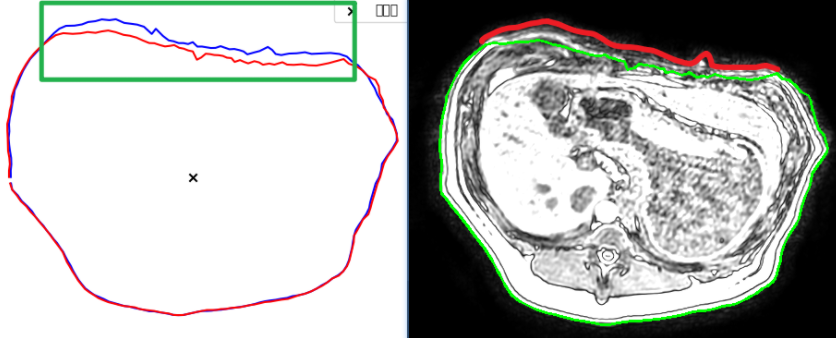
在数据集中的后边影像中,身体部分正常向外扩招,如上图蓝色区域,此时这部分会被检测为凹陷异常,那么就会用参考轮廓替代原本的蓝色轮廓。而且这种情况是累积的,因为身体向外扩展可能是连续的,所以如果当前层扩展失败,那么后面的更会失败,半径差会越来越大:
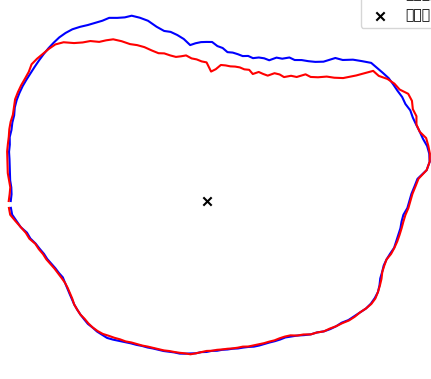
关键是”累积“的问题,这样抑制越来越大。
方案三:
方案三是方案一和方案二的结合。我们找到凹陷位置之后,[origin_li,origin_ri],计算凹陷的宽度,如果宽度大于50°,此时曲线拟合方式生成的点就不准确了。就直接好用参考轮廓上的对应点替代。
如果宽度小于50,就采用曲线拟合的方式
关于所有的思路到此结束
在记录python中函数传参引用的例子:
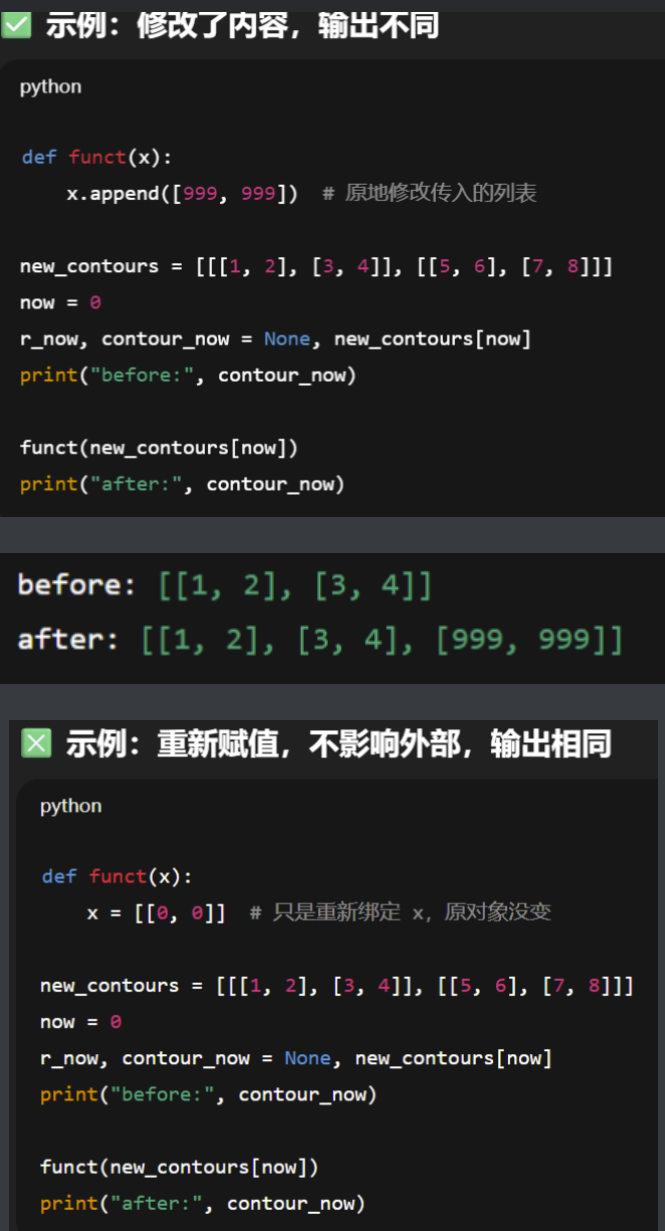
注意:这里是重新赋值,才不会影响外部。如果通过引用修改原本数据的值还是可以的,例如x[0] = 100.
完毕。
修补好皮肤轮廓之后就可以用这些轮廓进行表皮建模了。





















 3861
3861

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








