数据结构与算法-归并排序

归并的概念

“归并”一词的中文含义就是合并、并入的意思，而在数据结构中的定义是将两个或两个以上的有序表合成一个新的有序表。

归并排序的基本概念

归并排序（Merging Sort）就是利用归并的思想实现的排序方法。它的原理是假设初始序列含有n个记录，则可以看成n个有序的子序列，每个子序列的长度为1，然后两两归并，得到n/2向下取整个长度为2或1的有序子序列；再两两归并，······，如此重复，直至得到一个长度为n的有序序列为止。

java代码实现

/**
 * 将待排序列中的两个相邻有序子序列组合成一个
 * 
 * @param a	待排序序列
 * @param start	左边子序列的起始地址
 * @param mid	左边子序列的结束地址，mid+1是右边子序列的起始地址
 * @param end	右边子序列的结束地址
 * @param temp 	临时数组
 */
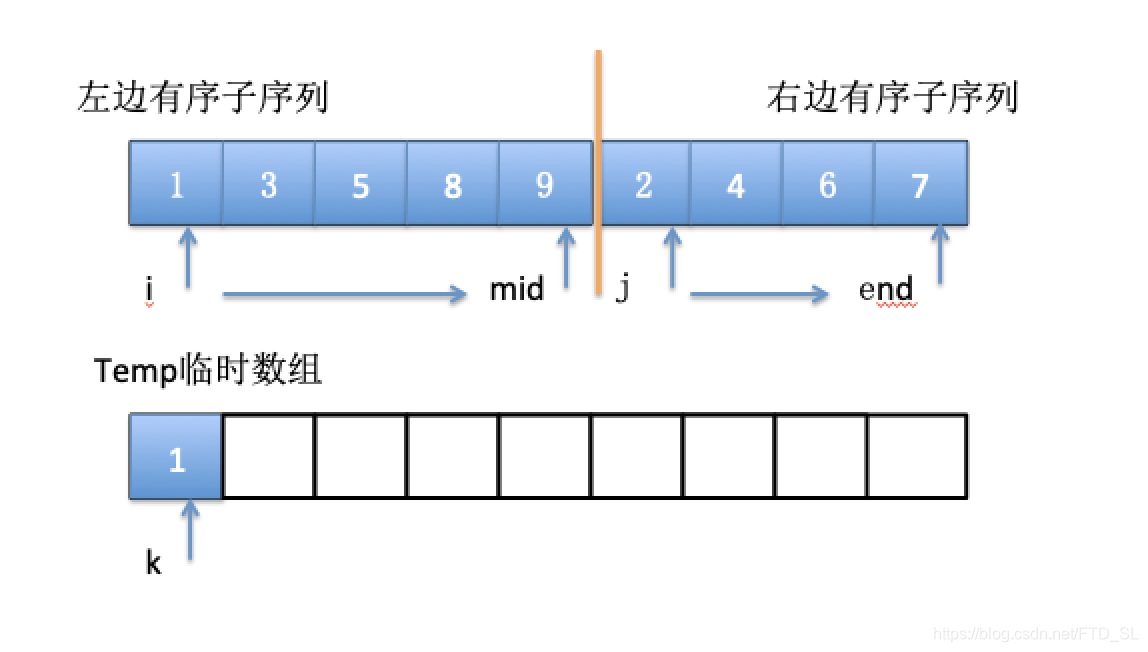
void merge(int[] a, int start, int mid, int end, int[] temp) {
	int i = start;   //左边子序列指针
	int j = mid + 1; //右边子序列指针
	int k = 0;       //临时数组指针
	while (i <= mid && j<= end) {
	    if (a[i] <= a[j]) { /* 取左子序列元素填充进temp，且左子序列指针后移一位 */
	       temp[k++] = a[i++];
	    } else { /* 取右子序列元素填充进temp，且右子序列指针后移一位 */
	       temp[k++] = a[j++];
	    }
	}
	/* 如果右子序列查询结束，则将左子序列中的剩余元素填充进temp中 */
	while (i <= mid) { 
	    temp[k++] = a[i++];
	}
	 /* 如果左子序列查询结束，则将右子序列中的剩余元素填充进temp中 */
	while (j <= end) {
	    temp[k++] = a[j++];
	}	
	/* 排序后的元素，全部整合到原待排序列中 */
	k = 0;
	while (start <= end) {
	    a[start++] = temp[k++];
	}
}

/**
 * 对待排序列进行若干次合并：将“每2个相邻的子元素”进行排序合并
 * 
 * @param a   待排序列
 * @param gap 每次合并时，子序列长度，1，2，4，8...
 */
 void merge_group(int[] a, int gap) {
	/* 申明临时数组，长度等于待排序列长度 */
	int[] temp = new int[a.length];
	int i;
	int twoLen = 2*gap; //两个相邻子序列长度
		
	/* 将“每2个相邻的子元素”进行排序合并 */
	for (i = 0; i+twoLen-1 < a.length; i+=twoLen) {
	    merge(a, i, i+gap-1, i+twoLen-1, temp);
	}
		
	/* 待排序列两两配对，若i+gap-1 < a.length-1，则剩余一个子序列没有配对。需要将该子序列排序合并到已排序列中 */
	if (i+gap-1 < a.length-1) {
	   merge(a, i, i+gap-1, a.length-1, temp);
	}
}

/**
 * 归并排序（递归方式）
 * 
 * @param a	待排序列
 * @param start	序列起始地址
 * @param end	序列结束地址
 */
void mergeSort_Recursion(int[] a, int start, int end) {
	/* 申明临时数组，长度等于待排序列长度，避免递归中频繁开辟空间 */
	int[] temp = new int[end-start+1];
	int mid = (start + end)/2;
	if (a == null || start >= end) { /* 递归终止条件 */
	    return;
	}
	mergeSort_Recursion(a, start, mid); /* 左边归并排序，使得左子序列有序 */
	mergeSort_Recursion(a, mid+1, end); /* 右边归并排序，使得右子序列有序 */
	merge(a, start, mid, end, temp);    /* 将最终的两个有序子序列归并排序 */
}

/**
 * 归并排序（迭代方式）
 * 
 * @param a 待排序列
 */
void mergeSort_Iteration(int[] a) {
     for (int n = 1; n < a.length; n*=2) { /* n以2的指数递增 */
	  merge_group(a, n);
     }
}

//声明待排序列
int[] a = {9,1,5,8,3,7,4,6,2};

//测试调用
//递归方式排序		
mergeSort_Recursion(a, 0, 8); //输出1,2,3,4,5,6,7,8,9
//迭代方式排序
mergeSort_Iteration(a); //输出1,2,3,4,5,6,7,8,9

图示代码执行过程

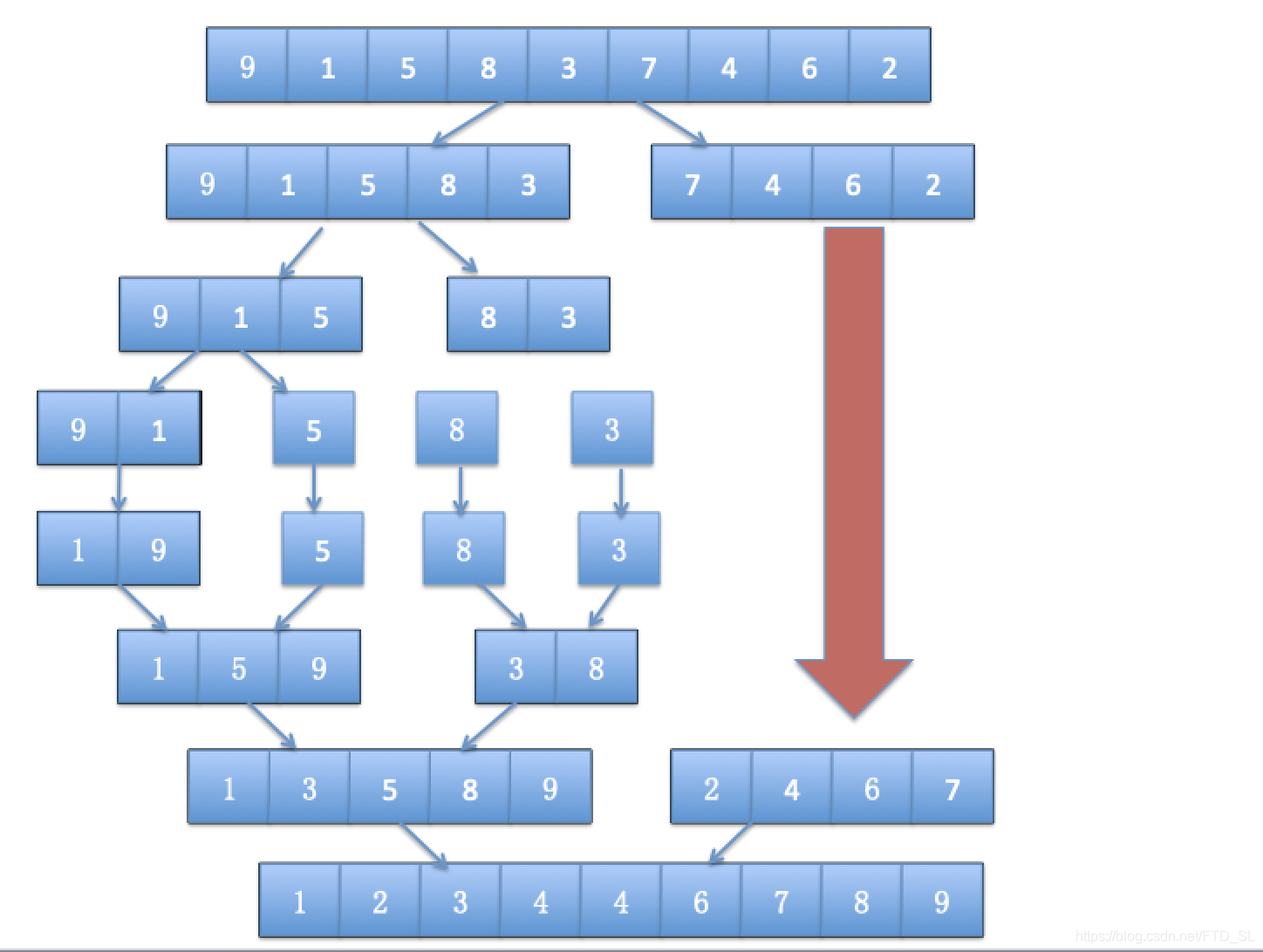
算法复杂度分析

• **递归方式：**一趟归并需要将待排序列中的所有记录扫描一遍，因此耗费O(n)时间，而由完全二叉树的深度可知，整个归并排序需要进行log₂n向下取整次，因此，总的时间复杂度为O(nlogn)，而且这是归并排序算法中最好、最坏和平均的时间性能。由于归并排序在归并过程中需要与原始记录列同样数量的存储空间存放归并结果及递归时深度为log₂n的栈空间，因此空间复杂度为0(n+logn)。
• **迭代方式：**非递归的迭代方法避免了递归时深度为log₂n的栈空间，空间只是用到申请归并临时用的数组，因此空间复杂度为O(n)，时间复杂度依然为O(nlogn)，但避免递归在时间性能上有一定的提升，所以使用归并排序时，尽量考虑用非递归方式。
• 分析代码可知，元素位置是通过a[i] <= a[j]两两比较进行调整，不存在跳跃，因此归并排序是一种稳定的排序算法。
• 总的来说，归并排序是一种比较占用内存，但却效率高且稳定的算法。