Partition相关整理

emmm迁移一下我的笔记好了...

partition 和single是对的

double是错误的

快排的partition算法

第一种是单向扫描法 - 算法导论

主要思想是，j 从 left 开始扫描，直到 j<right，这for循环过程中保证的是 i 及其左侧都是比 pivot 小的数

private static int partition(int[] arr, int left, int right) {
    int pivot = arr[right];
    int i=left-1;
    for(int j=left;j<=right-1;j++){  // for j left to right-1
        if(arr[j]<pivot){
            i++;
            if(i!=j)
            swap(arr,i,j);
        }
    }
    i++;
    swap(arr,i,right);
    return i;
}

第二种是双向扫描法，有多种具体实现办法，如下为“哨兵法”  fivejoy.github.io中记录 （当时记录时更理解挖坑填数法可见 也是很神奇哈哈）

private static int partition(int[] nums,int left,int right){
    int i=left;
    int j=right;
    int temp=nums[left];
    while(i<j) {   //！=也可以啊
        while(i<j&&nums[j]>temp)
            j--;
        while(i<j&&nums[i]<=temp)
            i++;
        if(i<j)
            swap(nums,i,j);
    }
    nums[left]=nums[i];
    nums[i]=temp;
    return i;
}

快排

public static void solution(int[] arr){
    if(null==arr||arr.length<2){
        return;
    }
    quickSort(arr,0,arr.length-1);
}

private static void quickSort(int[] arr, int left, int right) {
    if(left>=right)
        return;
    int g=partitionMOSINgle(arr,left,right);
    quickSort(arr,left,g-1);
    quickSort(arr,g+1,right);
}

快排时间复杂度

快速排序的最好情况：每次选取的主元可正好将数组a中的元素平均分成两份 每次将问题分为两个等分的问题然后向下递归T(N)=O(NlogN)
快速排序的最坏情况：每次选取的主元都将数组a分为1个元素+N-1个元素两份·

计算方法如下

 

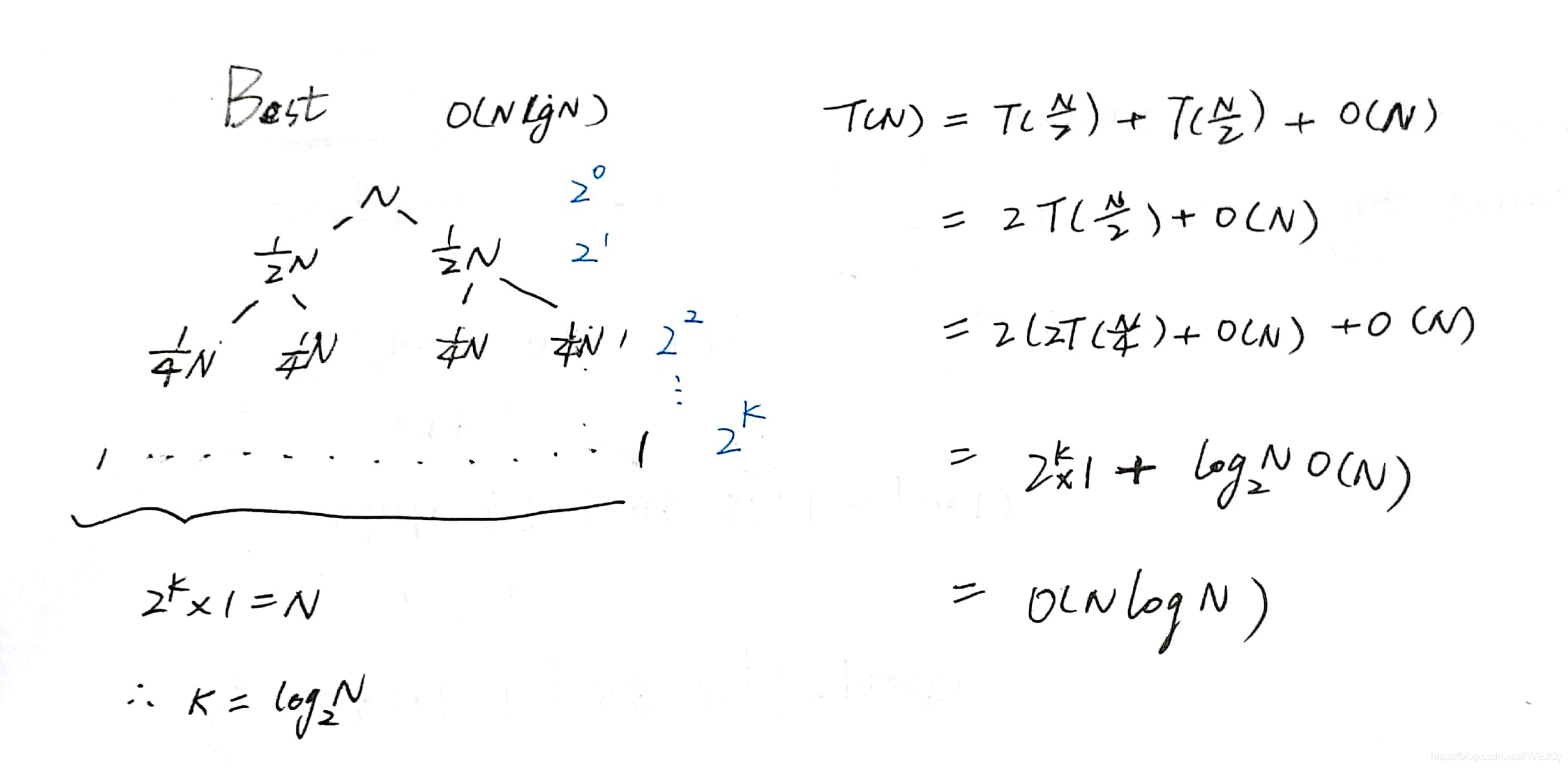
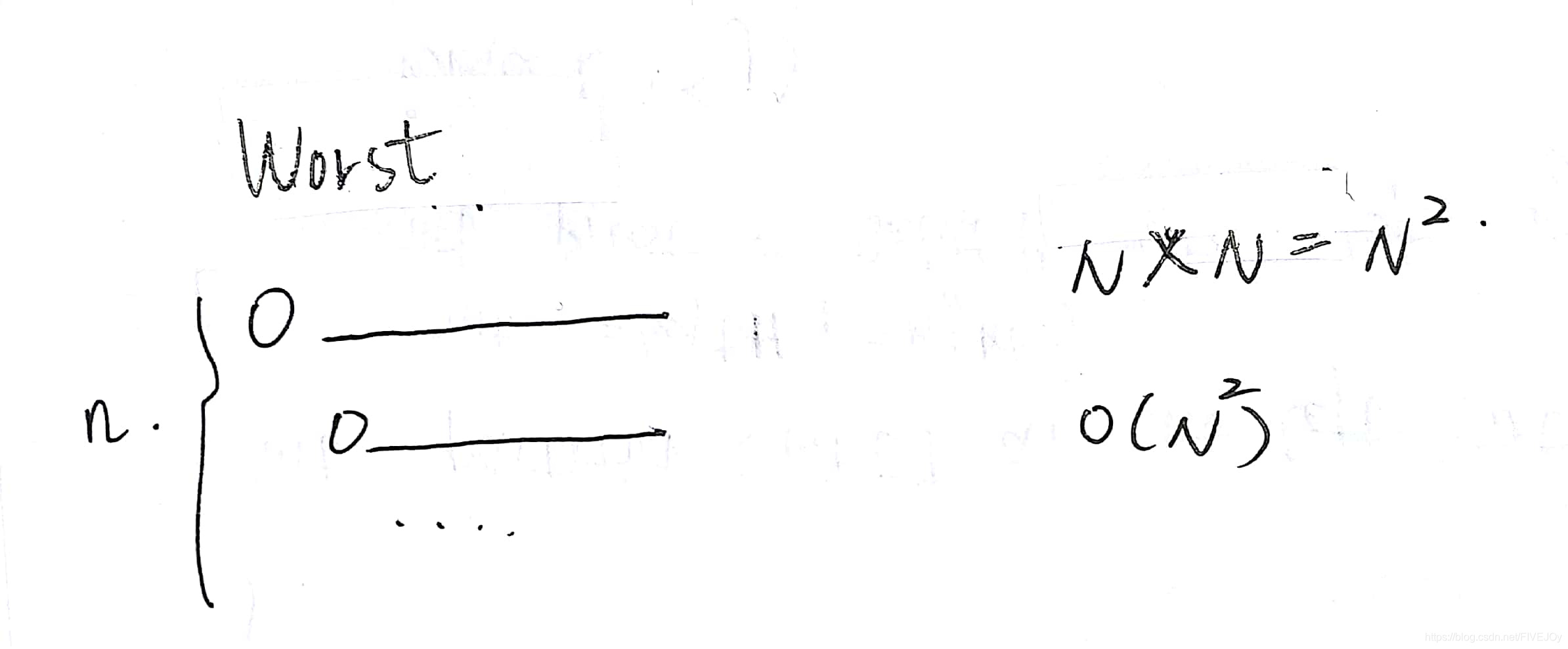
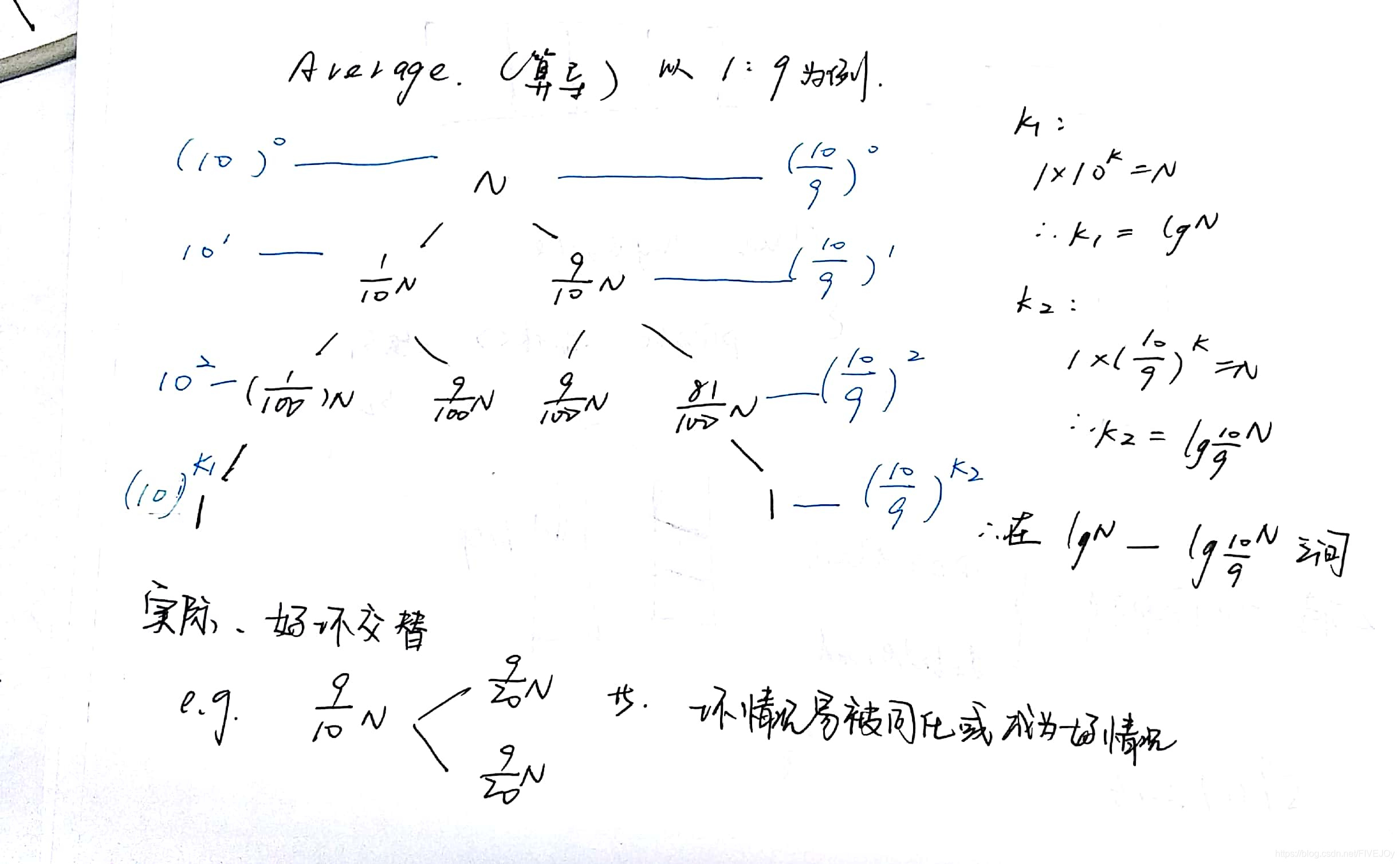
以下为快排中有必要了解的事情：

其中在partition选择pivot时，有多种方法，上面都选择的是取两侧，但是当序列有序时就比较容易出现最坏时间复杂度情况，即每次都是把序列分为N-1,1 的partition 。MOOC给出了其余三种选择方式

① 随机取pivot 但random()并不便宜

private static int selectPivot(int[] arr,int left,int right) {
    int i=left+(int)Math.random()*(right-left);
    swap(arr,left,i);
    return arr[i];
}

② 取 头中尾处元素 的中位数为pivot
③ 同理可以试试 5或者7个数取中位数

为什么插入排序比快排慢？

每次选择完pivot & 子集划分完后 ，pivot可被一次性放到其正确位置【保证最快！】。而在插入排序的每次交换中，元素所在的位置都是待定的，暂时的，可能下次循环又要后错一位【所以插入排序比快排慢咯】

如果有元素正好 = pivot 怎么办？MOOC
①停下并交换
所有元素都相等 eg. 1 1 1 1 1 1 1 ，此时会做出很多无谓的交换。但主元一定会换到比较中间的位置
② 不理它，继续移动。 但是最后主元会放到比较靠近边儿的位置—造成主元选取时①方法可能遇到的很囧的情况
SO所以选择① 吧

数据规模

快排对大规模数据做的不错，虽然归并和堆排也是O(NlgN)，但快排的常数项更小（nowcoder）

而在小规模数据中，因为采用递归，所以递归的弊端包括需要占用额外系统堆栈空间，每次调用系统堆栈时需要把很多东西压入栈中，返回时也不断POP。所以对（e.g. N<100）小规模数据可能并不如插入排序块 （插入排序的常数项低，所以当N不大时 O(N^2)<O(NlogN））

所以当数据规模未知时，可以设定一个cutOff阈值，小于阈值则使用简单排序算法，大于则使用快排。这个思想来自如Arrays.sort(),其使用的cutOff是60

 

以上两种partition实现的快排均经过随机数验证，验证方法如下

// for test
public static void comparator(int[] arr) {
    Arrays.sort(arr);
}

// for test
public static int[] generateRandomArray(int maxSize, int maxValue) {
    int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
    for (int i = 0; i < arr.length; i++) {
        arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
    }
    return arr;
}

// for test
public static int[] copyArray(int[] arr) {
    if (arr == null) {
        return null;
    }
    int[] res = new int[arr.length];
    for (int i = 0; i < arr.length; i++) {
        res[i] = arr[i];
    }
    return res;
}

// for test
public static boolean isEqual(int[] arr1, int[] arr2) {
    if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
        return false;
    }
    if (arr1 == null && arr2 == null) {
        return true;
    }
    if (arr1.length != arr2.length) {
        return false;
    }
    for (int i = 0; i < arr1.length; i++) {
        if (arr1[i] != arr2[i]) {
            return false;
        }
    }
    return true;
}

// for test
public static void printArray(int[] arr) {
    if (arr == null) {
        return;
    }
    for (int i = 0; i < arr.length; i++) {
        System.out.print(arr[i] + " ");
    }
    System.out.println();
}
public static void main(String[] args){
    int testTime = 500000;
    int maxSize = 100;
    int maxValue = 100;
    boolean succeed = true;
    int i=0;
    for ( i = 0; i < testTime; i++) {
        int[] arr1 = generateRandomArray(maxSize, maxValue);
        int[] arr2 = copyArray(arr1);
        solution(arr1);
        comparator(arr2);
        if (!isEqual(arr1, arr2)) {
            succeed = false;
            printArray(arr1);
            printArray(arr2);
            break;
        }
    }
    System.out.println("has been tested for "+i+"times");
    System.out.println(succeed ? "Congratulations!" : "Sorry Wrong !");
}

 

---

以下是partition算法的常见应用

应用一：

数组中出现次数超过一半的数字（就是一个数组中有一个数总是出现，出现次数甚至>arr.length/2）from 剑指offer 面试题29

解法一：先排序，最中间的数，使用快排的话时间复杂度O(nlogn) 

解法二： 基于partition算法，O(n) 会改变数组状态，因为用到了swap

同1中所想，若排序，则数组中间的数字必为出现次数最多的数，同时排序数组最中间的数，也就是整个数组中第length/2大的数

注意下面一句话要好好理解，才能明白怎么用partition做。

先对数组partition，获得选中pivot的下标为g ,如果g=N/2,则表示这个数字就是整个数组中第length./2.那如果g<N/2则表示所求数字一定在g的右侧，否则在左侧

无效情况：①传入数组为null ② 传入数组中最多出现的数出现次数并未超过一半

无效情况可以通过 返回0+使用全局变量 标记

boolean invalidArray=true;
public static int moreThanHalfNums(int[] a){
    int left=0,right=a.length-1,mid=left+(right-left)>>1;
    int g=partition(a,left,right);
    while(g!=mid) {
        if (g < mid) {
            left=g+1;
            g=partition(a,left,right);
        } else  {
            right=g-1;
            g=partition(a,left,right);
        }
    }
        int result=a[g];
        //检查一下这个数是不是真的出现了>N/2次
        checkInvaid(a,g);
        return result;
}

数组中第K的数字 int getKthMax(int[] a,int k)

同理，把上面的方法中的mid替换为K就可以了

解法三：根据数字出现次数的O(N)算法 eMm不是很好理解。。

遍历数组，声明temp,count

保存当前数字为temp，如果下一个数字和temp相同，则次数-1，如果相同，次数+1，如果数字为零，则保存下一个数字为temp，且将次数设为1.

由于要找的数字出现次数比其他所有数字出现次数之和大，因此要找的数一定是最后一个将count设置为1的temp

用例二 输出数组中最小的前K个数

解法一：partition算法 类似用例二中解法二的推广 ，but需要修改数组，否则就得用额外空间

解法二：O(Nlogk)  容器法

创建大小为K的数据容器

每次读一个数，如果容器未满，将数填入容器；如果容器已满，找到容器中最大的数，如果这个最大的数比当前数小，则丢弃当前数，否则替换。

所以对于这个容器来说，需要满足三种操作：① 找到最大数；②删除最大数；③ 插入新数

所以如果使用二叉树实现这个数据容器，则可以满足在O(logk)时间复杂度内实现这三步，对于N个数字，总时间O(Nlogk)

二叉树中的最大堆可以O(1)找到最大值 

解法二同时适用于海量数据输入，

由于内存大小有限，所以不能将海量数据一次性载入内存，这时可以从你辅助存储空间（硬盘每次读入数据），此时只要求内存能够容纳数据容器的大小即可。

如何利用数组实现最大堆。。。。。？