蓝桥杯2016A3.方格填数

最新推荐文章于 2021-04-12 19:22:56 发布

原创最新推荐文章于 2021-04-12 19:22:56 发布 · 221 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++

蓝桥专栏收录该内容

90 篇文章

订阅专栏

这篇博客探讨了一个有趣的数学问题，即如何在10个格子中填入0到9的数字，使得相邻的格子不含有连续的数字（包括上下左右和对角线方向）。作者通过C++编程，利用next_permutation函数进行全排列检查，最终得出有1580种不同的填数方案。博客内容主要涉及算法和编程技巧。

第二遍了。方法还会原来的配方，还是熟悉的味道。
如题：
如下的10个格子，填入0~9的数字。要求：连续的两个数字不能相邻。
（左右、上下、对角都算相邻）一共有多少种可能的填数方案？
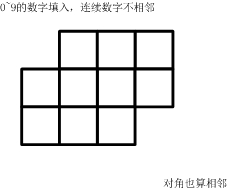
在这里插入图片描述
首先，我们先给格子分配好数字。

然后，代码如下：

#include<bits/stdc++.h>
using namespace std;
int a[11]={0,1,2,3,4,5,6,7,8,9};// 给这十个方格按顺序编号（下面有图） 
int judge()
{
	if(abs(a[0]-a[1])==1||abs(a[0]-a[3])==1||abs(a[0]-a[4])==1||abs(a[0]-a[5])==1||abs(a[1]-a[2])==1||abs(a[1]-a[4])==1||abs(a[1]-a[5])==1||abs(a[1]-a[6])==1||
	abs(a[2]-a[5])==1||abs(a[2]-a[6])==1||abs(a[3]-a[4])==1||abs(a[3]-a[7])==1||
	abs(a[3]-a[8])==1||abs(a[4]-a[5])==1||abs(a[4]-a[7])==1||abs(a[4]-a[8])==1||
	abs(a[5]-a[8])==1||abs(a[5]-a[9])==1||abs(a[4]-a[9])==1||abs(a[5]-a[6])==1||
	abs(a[6]-a[9])==1||abs(a[7]-a[8])==1||abs(a[8]-a[9])==1)
	return 0;
	return 1;
}
int main()
{
	int res=0;
	do
	{
		if(judge())
		{
			res++;
		}
	}
	while(next_permutation(a,a+10));//全排列来判断 
	cout<<res<<endl;
	return 0;
}