1/29 1631最小体力消耗路径

最新推荐文章于 2024-05-26 14:22:34 发布

原创最新推荐文章于 2024-05-26 14:22:34 发布 · 163 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#二分法 #算法 #leetcode

力扣专栏收录该内容

41 篇文章

订阅专栏

这篇博客介绍了如何运用二分查找算法解决一个寻找从地图左上角到右下角最小体力消耗路径的问题。作者通过示例解释了算法的思路，包括考虑路径上相邻格子高度差的绝对值，并给出了具体的代码实现。虽然作者最初尝试了并查集和全面排列的方法，但最终选择了二分法来解决这个复杂问题。

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往上，下，左，右四个方向之一移动，你想要找到耗费体力最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。

示例 1：

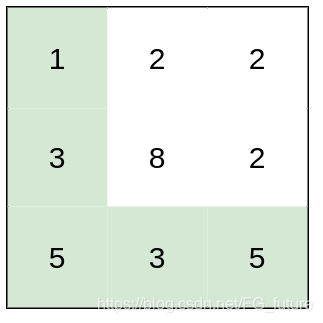
输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：

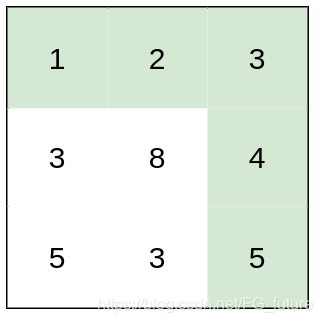
输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：
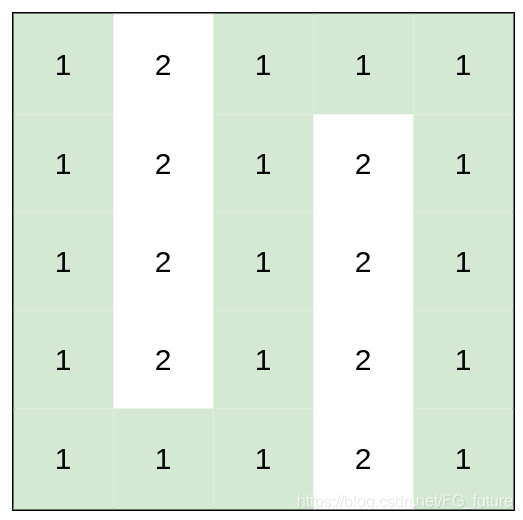
输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示 1. rows == heights.length
2. columns == heights[i].length
3. 3. 1 <= rows, columns <= 100
4. 4. 1 <= heights[i][j] <= 106

代码如下：

int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
//
int minimumEffortPath(int** heights, int heightsSize, int* heightsColSize) {
    int m = heightsSize;
    int n = heightsColSize[0];
    int left = 0, right = 999999, answer = 0;
    while (left <= right)
    {
        int mid = (left + right) / 2;
        int q[n * m][2];
        int qleft = 0, qright = 0;
        q[qright][0] = 0, q[qright++][1] = 0;
        int seen[m * n];
        memset(seen, 0, sizeof(seen));
        seen[0] = 1;
        while (qleft < qright)
        {
            int x = q[qleft][0], y = q[qleft++][1];
            for (int i = 0; i < 4; ++i)
            {
                int nx = x + dirs[i][0];
                int ny = y + dirs[i][1];
                if (nx >= 0 && nx < m && ny >= 0 && ny < n && !seen[nx * n + ny] && abs(heights[x][y] - heights[nx][ny]) <= mid)
                {
                    q[qright][0] = nx, q[qright++][1] = ny;
                    seen[nx * n + ny] = 1;
                }
            }
        }
        if(seen[m * n - 1]) 
        {
            answer = mid;
            right = mid - 1;
        } 
        else 
        {
            left = mid + 1;
        }
    }
    return answer;
}