1/22蓝桥杯求PI~

如题~

历史上有许多计算圆周率pai的公式，其中，格雷戈里和莱布尼茨发现了下面的公式：
pai = 4*(1-1/3+1/5-1/7 …)
参见【图1.png】
这个公式简单而优美，但美中不足，它收敛的太慢了。
如果我们四舍五入保留它的两位小数,那么：
累积1项是：4.00
累积2项是：2.67
累积3项是：3.47
…………
请你写出它累积100项是多少（四舍五入到小数后两位）。
注意：只填写该小数本身，不要填写任何多余的说明或解释文字。

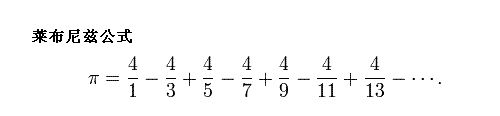
题比较简单，直接上代码

#include <stdio.h>
int main()
{
	double PI;
	int i;
	for(i=1;i<=100;i+=4)
	{
		PI+=1.0/i - 1.0/(i+2);
	}
	PI *= 4;
	printf("%.2f",PI);
 } 

运行截图如下：

答案是：3.12