扒开衣服看递归--递归的本质

编程语言中，函数Func(Type a,……)直接或间接调用函数本身，则该函数称为递归函数。
– 《百度百科》

我们一般运用递归算法来解决以下的几种问题：

1. 数据的定义是按递归定义的。（Fibonacci函数，n的阶乘）
2. 问题解法按递归实现。（回溯）
3. 数据的结构形式是按递归定义的。（二叉树的遍历，图的搜索）

可能到现在很多同学还没弄明白什么是递归，我们先来举个简单的例子。我的第一本计算机方面的书《C++程序语言设计》（谭浩强）中给出了一个这样的例子：

五个人坐在一起，第五个人比第四个人大2岁，第四个比第三个大2岁，每个人都比后面一个人大2岁，第一个人是10岁，问第五个人是几岁

我们脑海里很快想出了他们之间的关系：

age(5) = age(4) + 2;
age(4) = age(3) + 2;
age(3) = age(2) + 2;
age(2) = age(1) + 2;
age(1) = 10;

我们可以推导出一下的式子：

age(n) =  10   (n = 1)  //结束条件
age(n) = age(n - 1) +2 (n > 1) //推进条件。

每个递归函数总要具备两个条件：

1. 结束条件
2. 推进条件

结束条件用来告诉函数什么时候该停止，推进条件找出函数的一般条件，如本题的每个人比前面一个人大两岁，来进行函数推进。

我们可以写出以下的代码：

int age(int n)
{
   if(n == 1) c = 10;
   else return age(n - 1) + 2;
}

这段函数是怎么运作的呢，就是按照我们上面给出的递推关系，为了更好方便大家理解，画出一个递推的关系图。

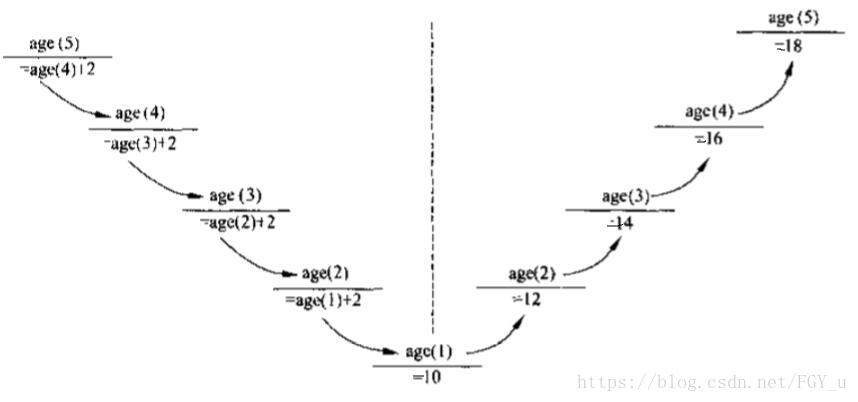
那么下面就来扒开衣服看本质，递归在内存中到底是怎么一种运作方式呢。根据上面的图，我们可以感觉到，递归的本质类似栈的性质，先进后出。

引用SpeedMe的一张图来解释。

函数的递归调用和普通函数调用是一样的。当程序执行到某个函数时，将这个函数进行入栈操作，在入栈之前，通常需要完成三件事。

1. 将所有的实参、返回地址等信息传递给被调函数保存。
2. 为被调函数的局部变量分配存储区。
3. 将控制转移到北调函数入口。

当一个函数完成之后会进行出栈操作，出栈之前同样要完成三件事。

1. 保存被调函数的计算结果。
2. 释放被调函数的数据区。
3. 依照被调函数保存的返回地址将控制转移到调用函数。

上述操作必须通过栈来实现，即将整个程序的运行空间安排在一个栈中。每当运行一个函数时，就在栈顶分配空间，函数退出后，释放这块空间。所以当前运行的函数一定在栈顶。