二叉搜索树(BSTree)

BST性质

二叉搜索树（Binary Search Tree，BST）是一种二叉树数据结构，也叫二叉排序树其中每个节点最多有两个子节点，通常称为左子树和右子树。二叉搜索树具有以下性质：

• 若左子树不为空，左子树所有结点的值都比根节点值小
• 若右子树不为空，右子树 所有结点的值都比根节点值大
• 根结点的左右子树也是二叉搜索树

比如下图是搜索二叉树

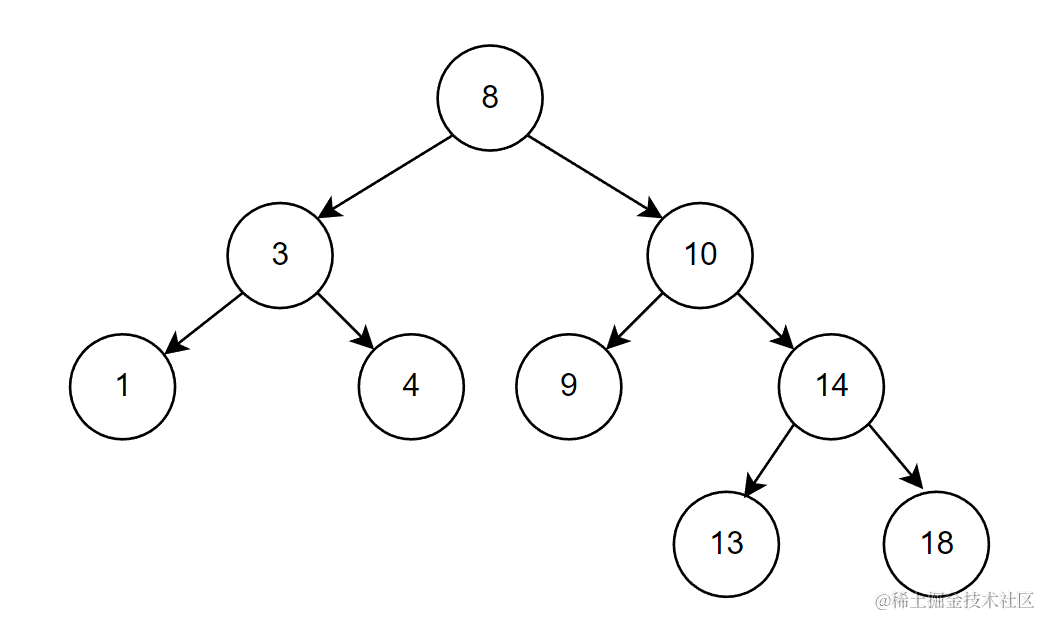
下图不是搜索二叉树(左子树值比根结点值大，不符合性质)

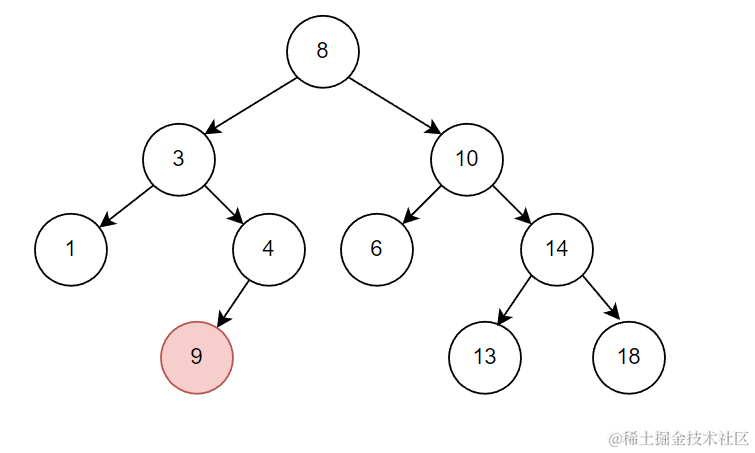
BST实现

实现BST，先构建一个结点类。结点需要三个成员变量，结点的值，左孩子和右孩子

template<class K>
struct BStreeNode
{
   
   
	BStreeNode<K>* _left;//左孩子
	BStreeNode<K>* _right;//右孩子
	K _key;//结点值
        //构造
	BStree(const K& key = K())
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
	{
   
   }
};

BST类接口

template<class K>
class  BSTree 
{
   
   
	typedef BStreeNode<K> Node;
public:
	//构造
	BSTree();

	//拷贝构造
	BSTree(const BSTree<K>& bst);

	//赋值运算符
	BSTree<K>& operator=(BSTree<K> t);

	//析构
	~BSTree();

	//插入
	void Insert(cosnt K& key);

	//删除
	void Erase(cosnt K& key);

	//查找
	Node* Find(cosnt K& key);
private:
	Node _root;
};

构造函数

初始化一个空的BST

BSTree()
    :_root(nullptr)
{
   
   }

拷贝构造函数

拷贝构造需要完成深拷贝，将现有的BST拷贝给一个新的BST即可，需要递归进行拷贝。而拷构造函数是成员函数
C++成员函数递归时，一般在套一层子函数进行递归

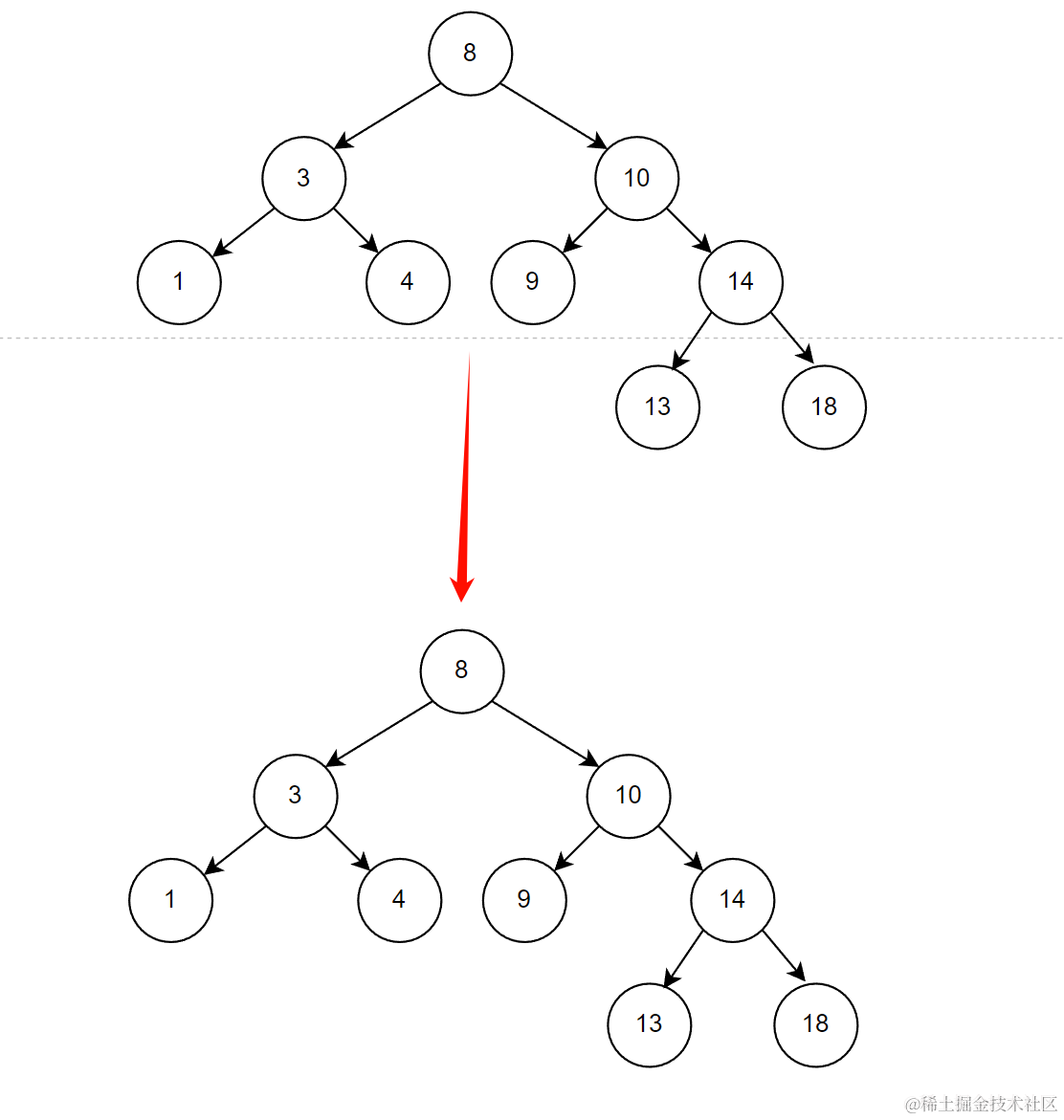
Node* _Copy(Node* root)
{
   
   
    if (root == nullptr)
    {
   
   
            return nullptr;
    }
    Node* node_copy = new Node(root->_key);
    node_copy->_left = _Copy(root->_left);//拷贝左子树
    node_copy->_right = _Copy(root->_right);//拷贝右子树
    return node_copy;
}
BSTree(const BSTree<K>& bst)
{
   
   
    _root = _Copy(bst._root);
}

赋值运算符重载

• 赋值时，如果当前对象有内容，应该先删除当前对象
• 在完成深拷贝

//释放时要自底向上释放，否则找不到左右孩子结点了
void _Destoy(Node* root)
{
   
   
    if (nullptr == root)
    {
   
   
            return;
    }
    _Destoy(root->_left);
    _Destoy(root->_right);
    delete root;
}
BSTree<K>& operator=(BSTree<K> t)
{
   
   
    if (&t != this)//防止自己给自己赋值
    {
   
   
            _Destory(this->_root);//删除当前对象
            _root = _Copy(t._root);
    }
}

析构函数

自底向上依次删除，最后置空即可

~BSTree()
{
   
   
    _Destory(_root);
    _root = nullptr;
}

插入元素

插入时，可以分为以下两种情况：

• 空树：直接将待插入元素做为根节点
• 非空：根据二叉树得性质进一步细分情况