1、回溯法概念
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。 回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。 许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
2、回溯法基本思想
在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)。 若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。而若使用回溯法求任一个解时,只要搜索到问题的一个解就可以结束。
3、回溯法解题的一般步骤
(1)针对所给问题,确定问题的解空间:
首先应明确定义问题的解空间,问题的解空间应至少包含问题的一个(最优)解。
(2)确定结点的扩展搜索规则
(3)以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索。
4、算法框架
(1)问题框架
设问题的解是一个n维向量(a1,a2,…,an),约束条件是ai(i=1,2,3,…,n)之间满足某种条件,记为f(ai)。
(2)非递归回溯框架
int a[n],i;
初始化数组a[];
i = 1;
while (i>0(有路可走) and (未达到目标)) // 还未回溯到头
{
if(i > n) // 搜索到叶结点
{
搜索到一个解,输出;
}
else // 处理第i个元素
{
a[i]第一个可能的值;
while(a[i]在不满足约束条件且在搜索空间内)
{
a[i]下一个可能的值;
}
if(a[i]在搜索空间内)
{
标识占用的资源;
i = i+1; // 扩展下一个结点
}
else
{
清理所占的状态空间; // 回溯
i = i –1;
}
}(3)递归的算法框架
回溯法是对解空间的深度优先搜索,在一般情况下使用递归函数来实现回溯法比较简单,其中i为搜索的深度,框架如下:
int a[n];
try(int i)
{
if(i>n)
输出结果;
else
{
for(j = 下界; j <= 上界; j=j+1) // 枚举i所有可能的路径
{
if(fun(j)) // 满足限界函数和约束条件
{
a[i] = j;
... // 其他操作
try(i+1);
回溯前的清理工作(如a[i]置空值等);
}
}
}
}回溯法有“通用解题法”之称。用它可以系统地搜索问题的所有解。回溯法是一个既带有系统性又带有跳跃性的搜索算法。
在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)。若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。 而若使用回溯法求任一个解时,只要搜索到问题的一个解就可以结束。
5、应用
下面的两棵解空间树是回溯法解题时常遇到的两类典型的解空间树。
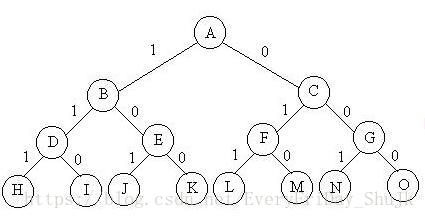
(1)当所给问题是从n个元素的集合S中找出S满足某种性质的子集时,相应的解空间树称为子集树。例如从n个物品的0-1背包问题(如下图)所相应的解空间树是一棵子集树,这类子集树通常有2^n个叶结点,其结点总个数为2^(n+1)-1。遍历子集树的算法需Ω(2^n)计算时间。
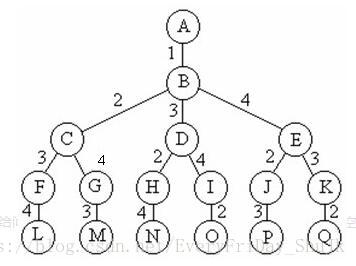
(2)当所给问题是确定n个元素满足某种性质的排列时,相应的解空间树称为排列树。例如旅行售货员问题(如下图)的解空间树是一棵排列树,这类排列树通常有n!个叶结点。遍历子集树的算法需Ω(n!)计算时间。
用回溯法搜索子集树的一般算法可描述为:
/**
* output(x) 记录或输出得到的可行解x
* constraint(t) 当前结点的约束函数
* bount(t) 当前结点的限界函数
* @param t t为当前解空间的层数
*/
void backtrack(int t){
if(t >= n)
output(x);
else
for (int i = 0; i <= 1; i++) {
x[t] = i;
if(constraint(t) && bount(t))
backtrack(t+1);
}
} 用回溯法搜索排列树的一般算法可描述为:
/**
* output(x) 记录或输出得到的可行解x
* constraint(t) 当前结点的约束函数
* bount(t) 当前结点的限界函数
* @param t t为当前解空间的层数
*/
void backtrack(int t){
if(t >= n)
output(x);
else
for (int i = t; i <= n; i++) {
swap(x[t], x[i]);
if(constraint(t) && bount(t))
backtrack(t+1);
swap(x[t], x[i]);
}
} (a)子集树
(为了便于描述算法,下列方法使用了较多的全局变量)
I.输出集合S中所有的子集,即limit为all;
II.输出集合S中限定元素数量的子集,即limit为num;
III.输出集合S中元素奇偶性相同的子集,即limit为sp。
public class Subset {
private static int[] s = {1,2,3,4,5,6,7,8};
private static int n = s.length;
private static int[] x = new int[n];
/**
* 输出集合的子集
* @param limit 决定选出特定条件的子集
* 注:all为所有子集,num为限定元素数量的子集,
* sp为限定元素奇偶性相同,且和小于8。
*/
public static void all_subset(String limit){
switch(limit){
case "all":backtrack(0);break;
case "num":backtrack1(0);break;
case "sp":backtrack2(0);break;
}
}
/**
* 回溯法求集合的所有子集,依次递归
* 注:是否回溯的条件为精髓
* @param t
*/
private static void backtrack(int t){
if(t >= n)
output(x);
else
for (int i = 0; i <= 1; i++) {
x[t] = i;
backtrack(t+1);
}
}
/**
* 回溯法求集合的所有(元素个数小于4)的子集,依次递归
* @param t
*/
private static void backtrack1(int t){
if(t >= n)
output(x);
else
for (int i = 0; i <= 1; i++) {
x[t] = i;
if(count(x, t) < 4)
backtrack1(t+1);
}
}
/**
* (剪枝)
* 限制条件:子集元素小于4,判断0~t之间已被选中的元素个数,
* 因为此时t之后的元素还未被递归,即决定之后的元素
* 是否应该被递归调用
* @param x
* @param t
* @return
*/
private static int count(int[] x, int t) {
int num = 0;
for (int i = 0; i <= t; i++) {
if(x[i] == 1){
num++;
}
}
return num;
}
/**
* 回溯法求集合中元素奇偶性相同,且和小于8的子集,依次递归
* @param t
*/
private static void backtrack2(int t){
if(t >= n)
output(x);
else
for (int i = 0; i <= 1; i++) {
x[t] = i;
if(legal(x, t))
backtrack2(t+1);
}
}
/**
* 对子集中元素奇偶性进行判断,还需元素的数组和小于8
* @param x
* @param t
* @return
*/
private static boolean legal(int[] x, int t) {
boolean bRet = true; //判断是否需要剪枝
int part = 0; //奇偶性判断的基准
for (int i = 0; i <= t; i++) { //选择第一个元素作为奇偶性判断的基准
if(x[i] == 1){
part = i;
break;
}
}
for (int i = 0; i <= t; i++) {
if(x[i] == 1){
bRet &= ((s[part] - s[i]) % 2 == 0);
}
}
int sum = 0;
for(int i = 0; i <= t; i++){
if(x[i] == 1)
sum += s[i];
}
bRet &= (sum < 8);
return bRet;
}
/**
* 子集输出函数
* @param x
*/
private static void output(int[] x) {
for (int i = 0; i < x.length; i++) {
if(x[i] == 1){
System.out.print(s[i]);
}
}
System.out.println();
}
} (b) 排列树
(为了便于描述算法,下列方法使用了较多的全局变量)
I.输出集合S中所有的排列,即limit为all;
II.输出集合S中元素奇偶性相间的排列,即limit为sp。
public class Permutation {
private static int[] s = {1,2,3,4,5,6,7,8};
private static int n = s.length;
private static int[] x = new int[n];
/**
* 输出集合的排列
* @param limit 决定选出特定条件的子集
* 注:all为所有排列,sp为限定元素奇偶性相间。
*/
public static void all_permutation(String limit){
switch(limit){
case "all":backtrack(0);break;
case "sp":backtrack1(0);break;
}
}
/**
* 回溯法求集合的所有排列,依次递归
* 注:是否回溯的条件为精髓
* @param t
*/
private static void backtrack(int t){
if(t >= n)
output(s);
else
for (int i = t; i < n; i++) { //没看懂没看懂
swap(i, t, s);
backtrack(t+1);
swap(i, t, s);
}
}
/**
* 回溯法求集合中元素奇偶性相间的排列,依次递归
* @param t
*/
private static void backtrack1(int t){
if(t >= n)
output(s);
else
for (int i = t; i < n; i++) {
swap(i, t, s);
if(legal(x, t))
backtrack1(t+1);
swap(i, t, s);
}
}
/**
* 对子集中元素奇偶性进行判断
* @param x
* @param t
* @return
*/
private static boolean legal(int[] x, int t) {
boolean bRet = true; //判断是否需要剪枝
//奇偶相间,即每隔一个数判断奇偶相同
for (int i = 0; i < t - 2; i++) {
bRet &= ((s[i+2] - s[i]) % 2 == 0);
}
return bRet;
}
/**
* 元素交换
* @param i
* @param j
*/
private static void swap(int i, int j,int[] s) {
int tmp = s[i];
s[i] = s[j];
s[j] = tmp;
}
/**
* 子集输出函数
* @param x
*/
private static void output(int[] s) {
for (int i = 0; i < s.length; i++) {
System.out.print(s[i]);
}
System.out.println();
}
} 本博客转载自 五大常用算法之四:回溯法
参考博客:
回溯法之递归回溯和迭代回溯
回溯法 最详细的介绍
手把手教你中的回溯算法——多一点套路





















 5734
5734

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








