import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
data=pd.read_table("kmeans_data.txt",header=None,names=['x','y'])
x=data['x']
y=data['y']
#绘图显示
plt.scatter(x,y)
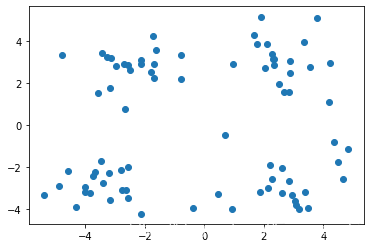
#data格式如下
data.head()
0 1.658985 4.285136
1 -3.453687 3.424321
2 4.838138 -1.151539
3 -5.379713 -3.362104
4 0.972564 2.92408
总共80行数据
#定义距离 求到一个center的距离
def distance(data,centers):
#data 80x2 centers:4x2 最终返回一个80x4的数据
dist=np.zeros((data.shape[0],centers.shape[0]))#先初始化一个空的80x4的矩阵 存放数据
#求80个点与4个随机初始化的点的欧式距离
for i in range(len(data)):
for j in range(len(centers)):
#data是pandas的数据格式 所以与array是不一样的 我们要取出来
dist[i,j]=np.sqrt(np.sum((data.iloc[i,:]-centers[j])**2))#欧式距离
return dist
def near_center(data,centers):
#求不同的点到不同center的距离
dist=distance(data,centers)
#求每一列的最小值
near_cen=np.argmin(dist,1)
#1表示是对列中进行寻找 返回80行 哪一列最小
#表示每一个点对应的距离哪个列最近 即离哪个点最近
return near_cen
#定义k-means函数
def kmeans(data,k):
#step1.随机给定簇中心k个 范围从-5 到5 取 小数为一位 大小为k行,2列
centers=np.random.choice(np.arange(-5,5,0.1),(k,2))
print(centers)
#第2 3进行迭代 10次
for _ in range(10):
#step2.点归属更新:数据点回归到距离它最近的簇上
near_cen=near_center(data,centers)
#step3. 簇重心更新
for ci in range(k):
centers[ci]=data[near_cen==ci].mean()#所有data中属于0类的数据
return centers,near_cen
centers,near_cen=kmeans(data,4)
print(centers)
print(centers[0])
plt.scatter(x,y,c=near_cen)
plt.scatter(centers[:,0],centers[:,1],marker="*",s=500,c='r')
#print("随机给定的4个中心",centers)
#dist=distance(data,centers)
#print("dist距离",dist)
#print("80个点分别距离哪个点最小",near_cen)
出现局部最优解的情况,这是kmeans的缺点
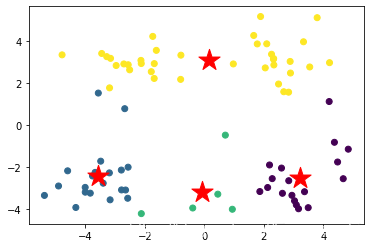
良好分类的情况
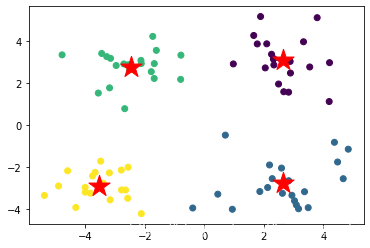
 K-means聚类实战
K-means聚类实战





 本文通过使用Python的NumPy、Matplotlib和Pandas库,详细介绍了如何实现K-means聚类算法。从数据读取到算法实现,再到结果可视化,全面展示了K-means的工作流程。同时,文中还探讨了K-means算法可能遇到的局部最优解问题。
本文通过使用Python的NumPy、Matplotlib和Pandas库,详细介绍了如何实现K-means聚类算法。从数据读取到算法实现,再到结果可视化,全面展示了K-means的工作流程。同时,文中还探讨了K-means算法可能遇到的局部最优解问题。
















 10万+
10万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








