力扣11 盛水最多的容器（java）

双指针法解决最大水量问题

最新推荐文章于 2024-08-04 23:34:29 发布

原创最新推荐文章于 2024-08-04 23:34:29 发布 · 362 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #java

该博客介绍了一个经典的计算机科学问题，即在给定一组高度不同的竖线中找到能容纳最多水的两条线。解决方案是使用双指针法，从数组的两端开始，移动高度较矮的指针来逐步计算并更新最大面积。这种方法优化了暴力求解的效率，通过不断调整高度较低的指针边界来最大化面积。

一、题目

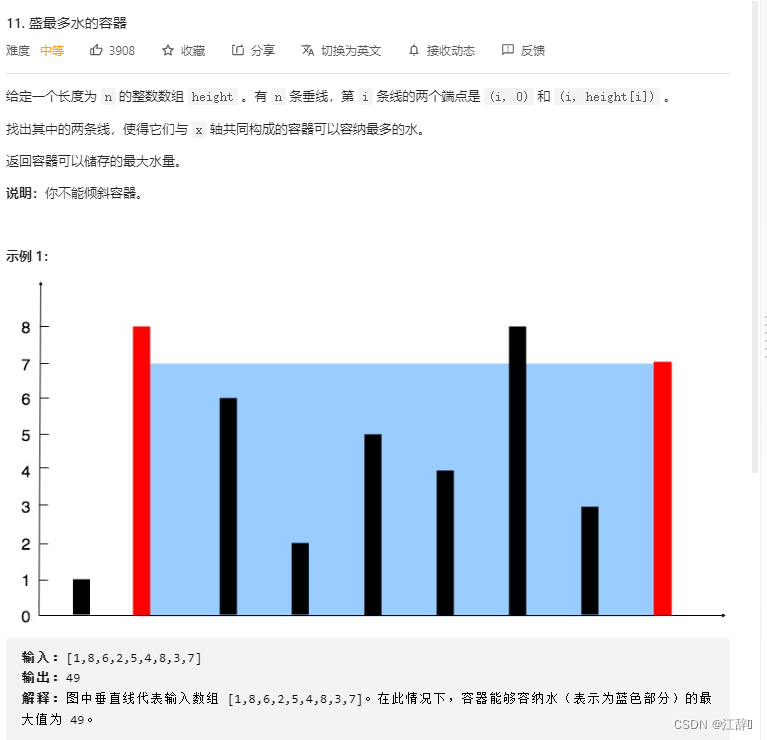
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
在这里插入图片描述

二、解法分析

可以采用暴力破解，暴力破解就是数组从左到右，数据两两组合，把所有的面积算出来取最大值。

（1）双指针法，下面是代码以及分析，分析在代码里和下面。

class Solution {
    public int maxArea(int[] height) {
        int left=0;
        int right = height.length-1; //首先定义两个指针
        int maxarea=0;		//定义最大面积，每次记录最大的面积，也就是最后输出结果
        while(left<right){	//定义一个循环，里面计算面积
       		 //求面积，
            //当前左右指针组成的面积currentarea=底*高  高是左右指针中高度最小的的那一个	
            int currentarea=(right-left)*Math.min(height[right],height[left]);
            //如果当前面积大于之前的最大面积，就替换掉
            if(currentarea>maxarea)
                maxarea = currentarea;
               //移动高度最小的那个指针。
            if(height[left]<height[right]){
                left++;
            }else
            right--;
        }
        return maxarea;
    }
}

（2）为什么移动高度最小的指针？

因为容器的面积是由高度最小的那个指针决定的。
如果移动高的指针，（假设右边的指针高度比左边的个指针高度高）那么移动后右边的指针高度比移动之前的右指针高度有可能大，也有可能小，无法判断面积。
所以移动高度低的指针，如果移动后的指针高度比原先的小，就不用替换原先的maxarea；
而如果移动后的左指针比移动前的大，计算出来面积去和原来的maxarea比较就可以了。