UVA679 Dropping Balls

小球下落 Dropping Balls

题目描述

许多的小球一个一个的从一棵满二叉树上掉下来组成一个新满二叉树，每一时间，一个正在下降的球第一个访问的是非叶子节点。然后继续下降时，或者走右子树，或者走左子树，直到访问到叶子节点。
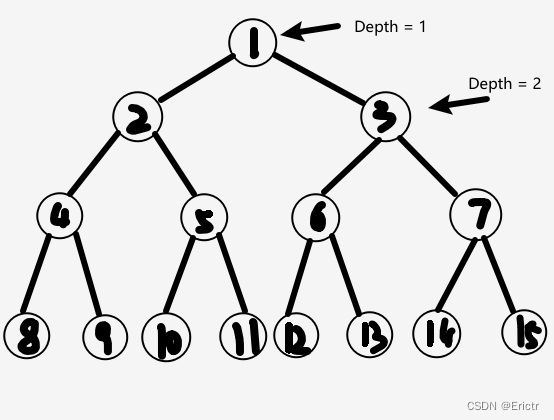
决定球运动方向的是每个节点的布尔值。最初，所有的节点都是 FALSE，当访问到一个节点时，如果这个节点是 FALSE，则这个球把它变成 TRUE，然后从左子树走，继续它的旅程。如果节点是TRUE，则球也会改变它为 FALSE，而接下来从右子树走。满二叉树的标记方法如下图。
因为所有的节点最初为 FALSE，所以第一个球将会访问节点 1，节点 2 和节点 4，转变节点的布尔值后在在节点 8 停止。第二个球将会访问节点 1、3、6，在节点 12 停止。明显地，第三个球在它停止之前，会访问节点 1、2、5，在节点 10 停止。
现在你的任务是，给定新满二叉树的深度 d 和下落的小球的编号 i ，可以假定I不超过给定的新满二叉树的叶子数，写一个程序求小球停止时的叶子序号p。

样例 #1

样例输入 #1

5
4 2
3 4
10 1
2 2
8 128
-1

样例输出 #1

12
7
512
3
255

分析

这道题比较直白，直接告诉我们是一个二叉树的题目，总体意思，就是相邻的两个小球在相同的节点处必然一个向左一个向右。根据题目给出的测试数据的大小，不难想到直接使用一个数组来模拟二叉树的想法，代码也很好写。

#include <iostream>
#include <cstring>
using namespace std;

bool nodes[1 << 20];

int main(int argc, char **argv){
	int cases = 0;
	cin >> cases;
	int D = 0, I = 0;
	while(true){
		
		cin >> D;
		if(D == -1){
			break;
		}
		cin >> I;
		memset(nodes, 0, 1<<D);
		int index = 0;
		while(I-- > 0){
			index = 0;
			while(2*index + 1 < (1<<D)-1){
				nodes[index] = !nodes[index];
				if(nodes[index]){
					index = 2*index + 1;
				}else{
					index = 2*index + 2;
				}
			}
		}
		cout << index+1 << endl;
	}
	return 0;
}

但是这样写会超时。
如果从另一个角度想，树是具有递归定义的，所以当小球从上一层调入下一层的时候，这时又是一个小球掉落的问题，只不过此时树的根节点变成了当前小球掉入的节点吗，此时我们只要更新一下 I 和 D，就能使用我们上述的算法再次解决该问题。
D的值表示树的深度，显然每一次树的深度是递减的，所以关键问题是怎么更新 I 的值？
根据题目的描述，对于树中的每一个节点，每经过2个小球，则该节点就恢复了原本的状况，也就是第奇数个小球到来的时候，就要走左子树，第偶数个小球到来的时候，就要走右子树。
分析得知，我们的问题变成了如何求到达该节点的小球是第几个(指奇偶)到达该节点的(说的好像有点拗口)。

• 如果 I 是偶数，则 I = I / 2
• 如果 I 是奇数，则 I = (I + 1) / 2

其实就是，经过该节点的小球个数比经过该节点父节点的小球个数少一半。
这样写出来，不需要创建一个很大的数组，而且是根据 I 的奇偶直接找到最后一个小球的路径。

#include <iostream>
using namespace std;

int main(int argc, char **argv){
	int cases = 0;
	cin >> cases;
	while(true){
		int D = 0;
		cin >> D;
		if(D == -1){
			break;
		}
		int I = 0;
		cin >> I;
		int index = 0;
		for(int i = 0; i < D; i++){
			if(2*index+1 >= (1<<D)-1){
				break;
			}
			if(I%2 == 0){
				I = I / 2;
				index = 2 * index + 2;
			}else{
				I = (I + 1) / 2;
				index = 2 * index + 1;
			}
			
		}
		cout << index+1 << endl;
	}
	return 0;
}