[蓝桥杯python]动态规划

最新推荐文章于 2025-07-31 17:52:10 发布

Osidal

最新推荐文章于 2025-07-31 17:52:10 发布

阅读量1.1k

点赞数 17

CC 4.0 BY-SA版权

分类专栏：蓝桥备赛算法文章标签：蓝桥杯动态规划职场和发展

本文链接：https://blog.youkuaiyun.com/Ensoleilef/article/details/138464480

文章讲述了动态规划在解决斐波那契数列、爬楼梯问题、最小花费路径、整数拆分、二叉搜索树计数、背包问题（01背包和完全背包）、零钱兑换和组合总和等经典问题中的应用，通过步骤详细讲解了状态转移方程、初始化和遍历顺序，强调了动态规划解决问题的思想和技巧。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

动态规划是一个难点，是值得认真钻研的。这里我推荐代码随想录讲的真心不错！能听懂，能学会！大家可以试试看。

What

动态规划：每个状态一定是由上一个状态推导出来的

贪心：没有状态推导，只是局部直接选最优

Steps

五部曲：

确定dp数组以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

常见类型

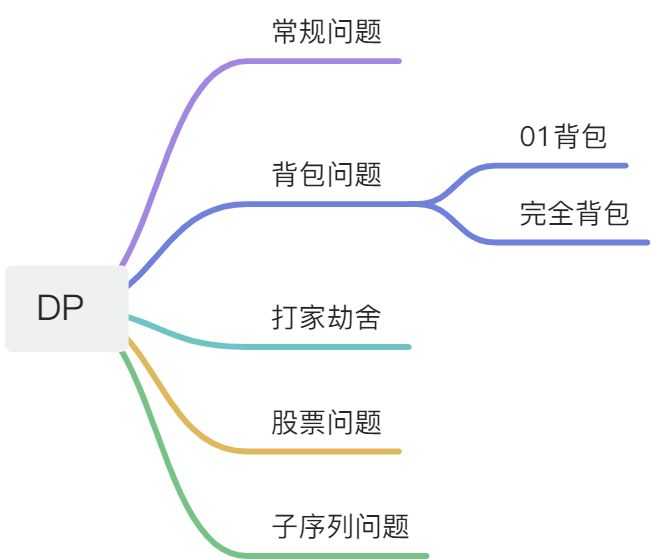
常规问题

斐波那契数列

class Solution:
    def fib(self, n: int) -> int:
        # 1. 确定dp数组的含义
        #  dp[i]:第i个斐波那契数的值
        # 2. 递推公式
        #  dp[i] = dp[i-1]+dp[i-2]
        # 3. 初始化
        # dp[0] = 0  dp[1] = 1
        # 4. 确定遍历顺序
        #  从前向后遍历
        # 5. 打印dp数组
        # debug作用

        dp = [0]*(n+1)
        if n <= 1: 
            return n
        else:
            dp[0] = 0
            dp[1] = 1
            for i in range(2,n+1):
                dp[i] = dp[i-1]+dp[i-2]
            return dp[n]

爬楼梯

class Solution:
    def climbStairs(self, n: int) -> int:
        # 1. 确定dp数组含义
        # dp[i] 达到第i节台阶有第dp[i]种方法
        # 2. 确定递推公式
        # dp[i] = dp[i-1] + dp[i-2]
        # 3. 初始化
        # dp[0] = 0 dp[1] = 1 dp [2] = 2
        # 4. 确定遍历顺序
        # 从头到尾
        # 5. 打印

        dp = [0]*(n+1)
        
        if n <= 1:
            return n
        else:
            dp[1] = 1
            dp[2] = 2
            for i in range(3,n+1):
                dp[i] = dp[i-1]+dp[i-2]
            return dp[n]

使用最小花费爬楼梯

状态转移方程

dp[i]表示的意思是：爬到第i层所需要的最低花费，

cost[i]表示的意思是：从楼梯第 i 个台阶向上爬需要支付的费用

对于dp[i] 求法应该是:

min(dp[i-1](在第i-1层时的最低花费)+cost[i-1](从第i-1层向上爬的费用),dp[i-2]+cost[i-2])

初始化

dp[0]和dp[1]都是0，这个地方稍微有点绕，题目说明了可以选择从第0层还是第1层开始爬，所以我们要站在第2层来看，到底是从1还是0层开始，看两者的花费那个更小，所以dp[2] = min(cost[0],cost[1])

下面是两种表示方法，可以体会一下不同，个人认为第一种方法比较好理解

class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        # 1. dp[i]:爬到第i层的最低花费
        # 2. dp[i] += min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
        # 3. 初始化dp[0] = 0 dp[1] = 0
        # 4. 遍历顺序: 从前到后

        dp = [0] * (len(cost)+1)
        dp[2] = min(cost[0],cost[1])
        for i in range(2,len(cost)+1):
            dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
        return dp[-1]