Problem of Precision（矩阵快速幂）

Link：http://acm.hdu.edu.cn/showproblem.php?pid=2256

Problem of Precision

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1083    Accepted Submission(s): 645

Problem Description

 

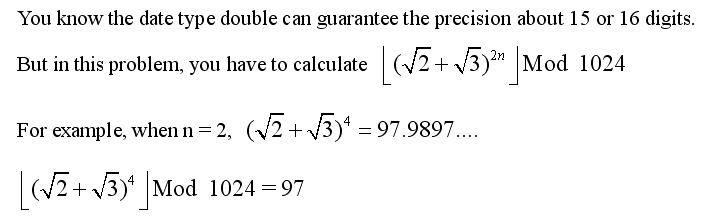
Input

The first line of input gives the number of cases, T. T test cases follow, each on a separate line. Each test case contains one positive integer n. (1 <= n <= 10^9)

 

Output

For each input case, you should output the answer in one line.

 

Sample Input

  
  

   
   3
1
2
5
  
  

 

Sample Output

  
  

   
   9
97
841
  
  

 

Source

HDOJ 2008 Summer Exercise（4）- Buffet Dinner

 

题意：求(sqrt(2) + sqrt(3)) ^ 2n MOD 1024。

编程思想：参考以下盗来的推公式的图

AC code：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<queue>
#include<map>
#define LL long long
#define MAXN 1000010
using namespace std;
const int INF=0x3f3f3f3f;
//----以下为矩阵快速幂模板-----//
const int mod=1024;
const int NUM=11;//定义矩阵能表示的最大维数
int N;//N表示矩阵的维数，以下的矩阵加法、乘法、快速幂都是按N维矩阵运算的
struct Mat{//矩阵的类
	int a[NUM][NUM];
	void init()//将其初始化为单位矩阵
	{
		memset(a,0,sizeof(a));
		for(int i=0;i<NUM;i++)
		{
			a[i][i]=1;
		}
	}
};
Mat add(Mat a,Mat b)//(a+b)%mod  矩阵加法
{
	Mat ans;
	for(int i=0;i<N;i++)
	{
		for(int j=0;j<N;j++)
		{
			ans.a[i][j]=a.a[i][j]+b.a[i][j];
			ans.a[i][j]%=mod;
		}
	}
	return ans;
}
Mat mul(Mat a,Mat b) //(a*b)%mod  矩阵乘法
{
	Mat ans;
	for(int i=0;i<N;i++)
	{
		for(int j=0;j<N;j++)
		{
			ans.a[i][j]=0;
			for(int k=0;k<N;k++)
			{
				ans.a[i][j]+=a.a[i][k]*b.a[k][j];
			}
			ans.a[i][j]%=mod;
		}
	}
	return ans;
}
Mat power(Mat a,int num)//(a^n)%mod  矩阵快速幂
{
	Mat ans;
	ans.init();
	while(num)
	{
		if(num&1)
		{
			ans=mul(ans,a);
		}
		num>>=1;
		a=mul(a,a);
	}
	return ans;
}
Mat pow_sum(Mat a,int num)//(a+a^2+a^3....+a^n)%mod 矩阵的幂和
{
	int m;
	Mat ans,pre;
	if(num==1)
		return a;
	m=num/2;
	pre=pow_sum(a,m);
	ans=add(pre,mul(pre,power(a,m)));
	if(num&1)
		ans=add(ans,power(a,num));
	return ans;
}
void output(Mat a)//输出矩阵
{
	for(int i=0;i<N;i++)
	{
		for(int j=0;j<N;j++)
		{
			printf("%d%c",a.a[i][j],j==N-1?'\n':' ');
		}
	}
}
//----以上为矩阵快速幂模板-----//
int main()
{
	int t,n,k,ans,i,j;
	int T;
	scanf("%d",&T);
	while(T--)
	{
	    scanf("%d",&n);
	    if(n==1)
        {
            printf("9\n");
            continue;
        }
		Mat a,f;
		N=2;
	    a.a[0][0]=5;
	    a.a[0][1]=12;
	    a.a[1][0]=2;
	    a.a[1][1]=5;
	    k=n%1024;//k为循环节
	    if(k==0)
            k=1024;
		f=power(a,k-1);
		int an=f.a[0][0]*5+f.a[0][1]*2;
		printf("%d\n",(2*an-1)%mod);
	 }
	return 0;
}