微信群红包模拟器-怎样抢最大的红包

最新推荐文章于 2022-12-14 13:48:29 发布

原创最新推荐文章于 2022-12-14 13:48:29 发布 · 1.9k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++

C++ 专栏收录该内容

3 篇文章

订阅专栏

本文通过建立微信红包模拟器，分析了红包分配的统计规律。使用C++实现模拟器，发现红包的期望值在平均值附近波动，但越往后抢，能获得的最大值越大。虽然平均值相同，但最后几个位置有更高的红包上限，揭示了抢红包的策略与位置的关系。

文章目录

1.前言
2.微信红包模拟器
3.统计结果分析
4.小结

1.前言

微信红包我们天天都在抢，既然是抢红包，我们当然希望是能抢到越多越好，最好是能成为运气王，睥睨群芳。那么怎么才能成为运气王，靠玄学还是靠技术？只要我们足够闲，手机足够多，发出大量的红包，最终能发现其中的统计规律，可以大胆的指出，次序与总人数成黄金分割比的那一位获得运气王的几率最大。

2.微信红包模拟器

当然如果知道了微信红包分配的算法，我们也可以自己写一个红包模拟器来分发红包，获得统计规律。恋猫大鲤鱼在他的博客中介绍了微信红包的随机分配策略。

每次抢红包直接随机，随机的范围是[1, 剩余红包金额均值的两倍]，单位分

具体为什么采取这样的分配策略，怎样保证公平可参见原博，这里我关心的是如何实现。
这里以C++为例进行实现，代码如下：

//
//  main.cpp
//  RedBag
//
//  Created by EngzSinger on 2021/3/1.
//

#include <iostream>
#include <vector>
#include <algorithm>
#include <stdlib.h>
#include <time.h>
#include <numeric>
#include <fstream>
#include <string>

using std::cout;
using std::cin;
using std::vector;
using std::endl;
using std::accumulate;
using std::ofstream;
using std::string;

/*
 * 定义一个红包分配器类
 */
class RedBagDistributor
{
private:
    int totalNum; //总红包个数
    int leftNum; //剩下的红包个数
    int balance; //余额
    int totalMoney; //红包总金额
    int minRand; //红包随机的下限
    int maxRand; //红包随机的上限，随剩余红包个数和余额的值更新
    int _Get_Luck_Not_Last(); //最后一个人的金额不是随机得到，所以这里将最后一个人和其他人的分配进行分别实现
    int _Get_Luck_Last();
    void _Remove_Bag();//封装leftNum-- 的操作
    void _Set_Max_Rand();//封装更新maxRand 的操作
    
public:
    RedBagDistributor() : totalNum(5),leftNum(5),balance(10000),totalMoney(10000),minRand(1),maxRand(4000) {srand((unsigned)time(NULL));}
    RedBagDistributor(int total_num,int total_money) :totalNum(total_num),leftNum(total_num),balance(total_money),totalMoney(total_money),minRand(1),maxRand(2*total_money/total_num) {srand((unsigned)time(NULL));}
    int GetLuck(); //抽取红包
    void ReSet(); // 重设模拟器，避免多次模拟过程中模拟器频繁构造析构带来的消耗
};

/*
 * 定义全局函数
 */
ofstream &print(ofstream &os,vector<int> vec)
{
    for(auto &a:vec)
    {
        os << a <<'\t';
    }
    os << endl;
    return os;
}
double average(vector<int> array)
{
    size_t num = array.size();
    int sum = accumulate(array.begin(),array.end(),0);
    //cout<<num<<'\t'<<sum;
    return double(sum)/double(num);
}

/*
 * 主函数
 * 进行10000次抢红包模拟，
 * 红包个数为10，红包总额为100元即10000分
 * 红包结果写入文件"Record.txt"中
 */
int main(int argc, const char * argv[]) {
    // insert code here...
    int bag_num = 10;
    int bag_sum = 10000;
    int frequency = 10000;
    string filename = "Record.txt";
    ofstream fout(filename);
    RedBagDistributor bador(bag_num,bag_sum);
    vector<vector<int>> RedBagRecord;
    RedBagRecord.resize(bag_num);
    for(auto &a:RedBagRecord)
    {
        a.resize(frequency);
    }
    for(int i=0;i<frequency;++i)
    {
        for(int j=0;j<bag_num;++j)
        {
            RedBagRecord[j][i]=bador.GetLuck();
        }
        bador.ReSet();
    }
    int tmp_counter = 0;
    for(auto &a:RedBagRecord)
    {
    	tmp_counter++;
    	cout<<"No."<<tmp_counter<<":"<<endl;
        cout<<"Average = "<<average(a)<<endl;
        cout<<"Max = "<<*max_element(a.begin(),a.end())<<endl;
        cout<<endl;
    }
    for(auto i=0;i<frequency;++i)
    {
        vector<int> tmp;
        for(auto j=0;j<bag_num;++j) tmp.push_back(RedBagRecord[j][i]);
        print(fout,tmp);
    }
    return 0;
}

/*
 * 类内函数的实现
 */
void RedBagDistributor::_Remove_Bag()
{
    leftNum--;
}
int RedBagDistributor::_Get_Luck_Not_Last()
{
    auto get_value = (rand() % (maxRand-minRand+1))+minRand;
    balance -= get_value;
    _Remove_Bag();
    return get_value;
}
int RedBagDistributor::_Get_Luck_Last()
{
    _Remove_Bag();
    return balance;
}

int RedBagDistributor::GetLuck()
{
    //if(leftNum==0) //exception
    _Set_Max_Rand();
    if(leftNum==1)
        return _Get_Luck_Last();
    else
        return _Get_Luck_Not_Last();
}
void RedBagDistributor::_Set_Max_Rand()
{
    maxRand = 2*(balance/leftNum);
}
void RedBagDistributor::ReSet()
{
    leftNum = totalNum;
    balance = totalMoney;
    _Set_Max_Rand();
    //srand((unsigned)time(NULL));//秒级时间，程序运行过程中没有变化
}

3.统计结果分析

首先是程序在标准输出设备的输出信息，可以看到对于每一个参与抢红包的人，所能获得红包的期望都在总体平均值附近浮动，这也比较符合红包设计的初衷，尽量保证分配过程的公平。细心观察不难发现，其中第六位能获得红包的平均值为1015.24，在所有人中比较突出，我们选择的总人数为10人，黄金分割位正好是第六个，所以充分验证我们开篇的猜想！当然不是，我差点都信了，这只是一个巧合，多运行几次结果就不是第六个的平均值最大了。
平均值大家都一样，而最大值就比较有意思了，可以发现越往后能获得的最大值越大。其实这也好理解，随机范围的最大值是剩余均值的两倍，假设前面的人抢到的数值足够小，那么越往后剩余均值越大，对应的随机范围最大值也越大。

No.1:
Average = 991.353
Max = 2000

No.2:
Average = 998.175
Max = 2214

No.3:
Average = 1001.36
Max = 2439

No.4:
Average = 1001.67
Max = 2760

No.5:
Average = 997.317
Max = 3067

No.6:
Average = 1015.24
Max = 3240

No.7:
Average = 1007.83
Max = 3771

No.8:
Average = 995.736
Max = 4383

No.9:
Average = 988.318
Max = 5148

No.10:
Average = 1003
Max = 5956

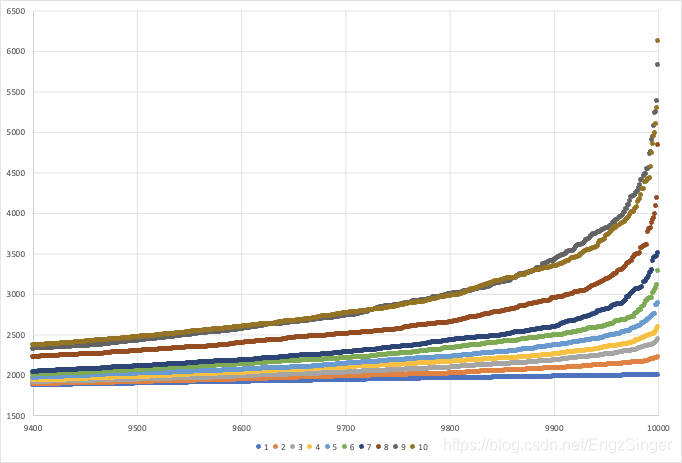
前面只是看到了每一位最大值，结果具有随机性，为了能看到更广泛的分布，我们可以把输出到文件的内容在Excel中进行处理，将每个位置对应的所有红包进行排序，绘制不同位置的红包散点图，看每个位置能拿到红包中最大若干个值的比较。可以看到位置越往后，获得的红包值上限越大。

4.小结

不管排在那个位置，获得红包的期望都是总体均值，但是越往后能获得的最大值越大，换言之，越往后越刺激。
按照红包分配策略，最后一个人能拿到的是倒数第二个人抢完后的余额，两个人的红包应该差不多，但是从图中可以看出第九个人与第十个是相比有一点略微的优势。是因为统计样本不够大，还是因为数学原理掌控了结果？
本文实现的模拟器放弃了对最后一个红包的限制，导致最后一个人可能抢到0元，如何优雅的解决这个问题。