动态规划 - 直方图的水量 - 困难

*************

C++

topic：面试题 17.21. 直方图的水量 - 力扣（LeetCode）

***********

直接看题：

这个一定是要用到指针的，因为需要比较指针两端的最大高度和中间的差值，这样才能判断中间是不是能存水。

暴力美学，the aesthetics of violence，没有思路的时候，就直接手搓代码，帮助我理清思绪。这个题是真的有点难度的，我想了很长时间都没有思绪。

先想一下怎么存水，如果一个柱子两边的柱子都比它高，那么它就可以存水，存水量等于两边柱子中较矮的那个柱子的高度减去当前柱子的高度，这个是算法的核心，当然这个很好理解。对于每一个位置i，如果它的左边最高的柱子和右边最高的柱子都比它高，那么这个位置可以存水，存水量等于min(左边最高，右边最高) - height[i]。因此，初步解决方案：对于每个位置i，找到它左边的最高柱子和右边的最高柱子，然后计算min(left_max, right_max) - height[i]，累加所有这样的值，就是总的存水量。

首先回想一下，我之前做过的题目，有没有相关的，类似的题目，子序列不是的，哈希表也不像，因为不需要查找不一样的元素，这个题目的里面是可以包含一样的。

没有思绪，上 暴力美学，永远可以相信暴力美学：

.size	0	1	2	3	4	5	6	7	8	9	10	11
s	0	1	0	2	1	0	1	3	2	1	2	1

1. 初始化一个变量total_water来存储总的存水量，初始值为0。

2. 遍历数组中的每一个位置i：

    a. 找到i左边最高的柱子left_max。

    b. 找到i右边最高的柱子right_max。

    c. 计算当前存水量current_water = min(left_max, right_max) - height[i]。

    d. 如果current_water > 0，将current_water加到total_water中。

3. 返回total_water。

OK，看起来可行，直接写代码：

首先完成第一步：

class Solution {
public:
    int trap(vector<int>& height) {
        int total_water = 0; // Step 1: Initialize total_water
        int n = height.size();
        if (n == 0) return 0;

        vector<int> left_max(n, 0); // initialise the max heught equals 0
        vector<int> right_max(n, 0); // so is the right one

        
    }
};

这里有个小细节，就是

vector<int> left_max(n, 0); // initialise the max heught equals 0

vector<int> right_max(n, 0); // so is the right one

初始化成为向量，这样就可以直接用 left_max[i]表示 i 位置的左边的最高值。

然后找到当前位置的左侧的最大值和右侧的最大值:

class Solution {
public:
    int trap(vector<int>& height) {
        int total_water = 0; // Step 1: Initialize total_water
        int n = height.size();
        if (n == 0) return 0;

        vector<int> left_max(n, 0);
        vector<int> right_max(n, 0);

        // find max
       
        for (int i = 1; i < n; ++i) {
            left_max[i] = max(left_max[i - 1], height[i]);
        }

       
        for (int i = n - 2; i >= 0; --i) {
            right_max[i] = max(right_max[i + 1], height[i]);
        }

       
    }
};

遍历所有位置，并求个和：

class Solution {
public:
    int trap(vector<int>& height) {
        int total_water = 0; // Step 1: Initialize total_water
        int n = height.size();
        if (n == 0) return 0;

        vector<int> left_max(n, 0);
        vector<int> right_max(n, 0);

        // find max
       
        for (int i = 1; i < n; ++i) {
            left_max[i] = max(left_max[i - 1], height[i]);
        }

      
        for (int i = n - 2; i >= 0; --i) {
            right_max[i] = max(right_max[i + 1], height[i]);
        }

        // go through every position
        for (int i = 0; i < n; ++i) {
            // caculate current 
            int current_water = min(left_max[i], right_max[i]) - height[i];
            // 如果current_water > 0，将current_water加到total_water中
            if (current_water > 0) {
                total_water += current_water;
            }
        }

        return total_water; 
    }
};

不出意外的，又错了

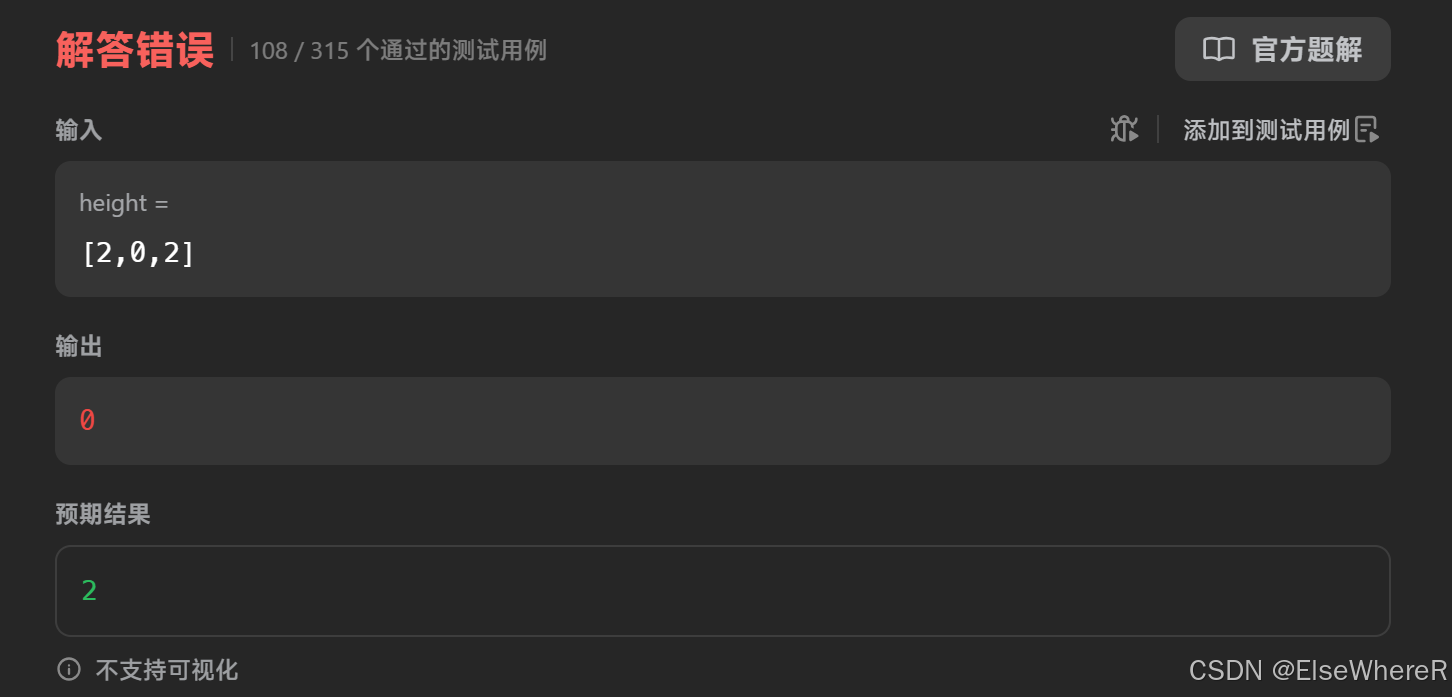
这个答案一看就是2，为什么算出来是0呢？

按照代码跑一遍：

n = 3

i = 1

left_max[0] = max(left_max[0], height[1],

问题吹在了这里，没有left_max[0]

初始化left_max[0] = height[0].

class Solution {
public:
    int trap(vector<int>& height) {
        int total_water = 0; // Step 1: Initialize total_water
        int n = height.size();
        if (n == 0) return 0;

        vector<int> left_max(n, 0);
        vector<int> right_max(n, 0);

        // find max
        left_max[0] = height[0];
        for (int i = 1; i < n; ++i) {
            left_max[i] = max(left_max[i - 1], height[i]);
        }

        right_max[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; --i) {
            right_max[i] = max(right_max[i + 1], height[i]);
        }

        // go through every position
        for (int i = 0; i < n; ++i) {
            // caculate current 
            int current_water = min(left_max[i], right_max[i]) - height[i];
            // 如果current_water > 0，将current_water加到total_water中
            if (current_water > 0) {
                total_water += current_water;
            }
        }

        return total_water; 
    }
};

OK，这个可以run，比较的成功。

动态规划还是好啊。