《N-gram模型》的补充修正

由前一篇转载的文章可知，N-Gram 该模型基于这样一种假设，第n个词的出现只与前面N-1个词相关，而与其它任何词都不相关，整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计N个词同时出现的次数得到。常用的是二元的Bi-Gram和三元的Tri-Gram。 如果一个词的出现仅依赖于它前面出现的一个词，那么我们就称之为bi-gram。如果一个词的出现仅依赖于它前面出现的两个词，那么我们就称之为tri-gram。

补充修正：

前一篇转载的文章称，“那么我们怎么得到P(Wn|W1W2…Wn-1)呢？一种简单的估计方法就是最大似然估计(Maximum Likelihood Estimate）了。即P(Wn|W1W2…Wn-1) = (C(W1 W2…Wn))/(C(W1 W2…Wn-1))“（*）式

个人认为此处并没有用到最大似然估计，而仅仅是使用了简单的条件概率密度公式，P(A|B)=P(AB)/P(B)。（害楼主看原文时迷糊了好久><）

即P(Wn|W1W2…Wn-1) = (P(W1 W2…Wn))/(P(W1 W2…Wn-1))=(C(W1 W2…Wn))/(C(W1 W2…Wn-1))，其中C(W1 W2…Wn)为序列W1 W2…Wn的统计次数。

补充知识：最大似然估计的概念。

给定一个概率分布，假定其概率密度函数（连续分布）或概率质量函数（离散分布）为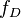，以及一个分布参数，我们可以从这个分布中抽出一个具有个值的采样，通过利用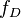，我们就能计算出其概率：

显然，最大似然估计的目的在于通过确定的n个采样值X1，X2，... ，XN来估计未知而确定的分布参数。这也说明（*）式并没有用到最大似然估计。

设样本是独立地从p(x|)中抽取的，所以在概率密度为p(x|)时获得样本集X={X1，X2，... ，XN}的概率即出现X中各个样本的联合概率：

l()=p(X1，X2，... ，XN|)

其对数似然函数表示为：H()=lnl()

最大似然估计的求解：在似然函数满足连续、可微的条件下，如果是一维变量，最大似然估计量是如下微分方程的解：

dl()/d()=0

或dH()/d()=0

方程组的解即是似然函数的极值点，其中使得似然函数最大的那个解才是最大似然估计量。

欢迎讨论！