【题解】剑指 Offer II 092. 翻转字符（字符串）（动态规划）

题目链接

 力扣

题目描述

如果一个由 '0' 和 '1' 组成的字符串，是以一些 '0'（可能没有 '0'）后面跟着一些 '1'（也可能没有 '1'）的形式组成的，那么该字符串是 单调递增 的。

我们给出一个由字符 '0' 和 '1' 组成的字符串 s，我们可以将任何 '0' 翻转为 '1' 或者将 '1' 翻转为 '0'。

返回使 s 单调递增 的最小翻转次数。

示例 1：

输入：s = "00110"
输出：1
解释：我们翻转最后一位得到 00111.
示例 2：

输入：s = "010110"
输出：2
解释：我们翻转得到 011111，或者是 000111。
示例 3：

输入：s = "00011000"
输出：2
解释：我们翻转得到 00000000。
 

提示：

1 <= s.length <= 20000
s 中只包含字符 '0' 和 '1'

解题思路

 首先看到这个题，根据经验能判断出来是动态规划，第一反应有点像编辑距离问题力扣，但是看了看给定的数据范围，不能让我们按照字符串长度建立二维的dp数组，所以就考虑能不能二维数组一维是字符串的长度，一维代表0和1，参考了一下题解，可以推出转移方程

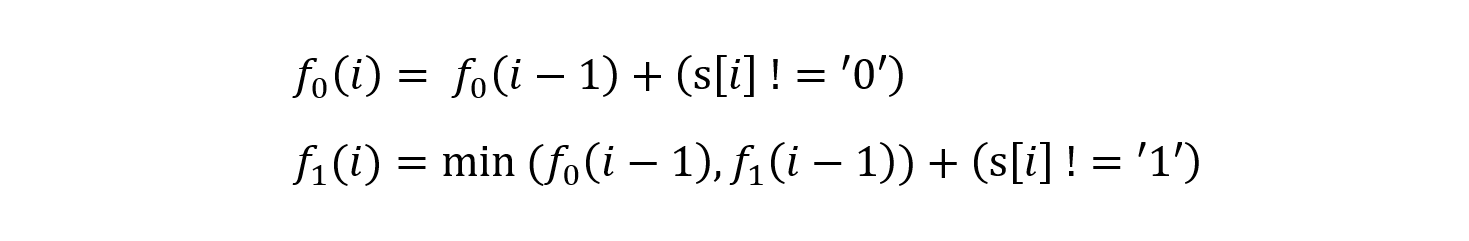
其中f0(i)和f1(i)是代表修改后这一位是0还是1的

        当当前位为0的时候，满足题意的只有前面的位数都为0的时候，然后判断这一位本身是不是0，不是的话需要增加一步从1变0的次数

        当当前为为1的时候，满足题意可以前一位是0或者前一位是1，只需要在两者之间选个最小的就可以了，然后判断这一位本身是不是1，不是的话需要增加一部从0变1的次数

题解

class Solution {
public:
    int dp[20005][2];
    int minFlipsMonoIncr(string s) {
        dp[0][1]=s[0]=='1'?0:1;
        dp[0][0]=!dp[0][1];
        for(int i=1;i<s.length();i++){
            dp[i][0]=dp[i-1][0]+(s[i]=='0'?0:1);
            dp[i][1]=min(dp[i-1][0],dp[i-1][1])+(s[i]=='1'?0:1);
        }
        return min(dp[s.length()-1][0],dp[s.length()-1][1]);
    }
};