【算法】【动态规划】最长上升子序列和最长不下降子序列

也是个动态规划的经典问题了

 

参考视频：9.67 最长不下降子序列——信息学竞赛培训课程_哔哩哔哩_bilibili

给出一个无序的数组

例如：5 8 8 6 2 6 7

则最长上升子序列为5 6 7

最长不下降子序列为5 6 6 7

核心思想：遍历数组，以被遍历的数为结尾计算最长序列

最长上升子序列

逐步遍历：

1.先设置一个dp数组，初值全部设为1 

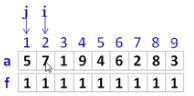
设置两个变量i,j，j不能大于i，如果a[j]<a[i]，则f[i]取f[i]和f[j]+1的最大值

转化为代码就是

for(int i=0;i<n;i++){
	for(int j=0;j<i;j++){
		if(a[j]<a[i]){
			f[i]=max(f[i],f[j]+1);
		}
	}
} 

时间复杂度：O（n²） 

注意：必须前面的所有数据都遍历一遍，不能让j=i然后倒着开始，碰到就break

因为可能有这种情况

5

7

1

9

4

6

2

8

3

拿9举例，正确选项应该是7，有两个，要是按照上面的方法就只有1一个了 

最长不下降子序列

将判断中的

if(a[j]<a[i])

改为

if(a[j]<=a[i])

 即可