动态规划--入门教程

原创

已于 2024-11-18 11:16:31 修改 · 958 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划

于 2020-07-30 23:49:06 首次发布

文章目录

基本动态规划
Max Sum
数塔
滑雪
Monkey and Banana
LIS问题
LCS问题
最短编辑距离
编辑距离

基本动态规划

动态规划是将一个问题分解成若干个同一系列的决策的结果，贪心准则是做出一个不可撤回的决策，然而动态规划要考察每个最优的决策序列是否包含一个最优子序列。如果一个问题具有最优子序列具有最优子结构时，要学会用动态规划的思路去解决，把当前的选择看作是最优的决策。贪心算法当前选择依赖于过去的决策，但是不依赖于未来的决策，也不依赖于子问题的解。

斐波那契数列 $F (n)$
递归版本

int f(int n)
{
   
   
    if(!n || n==1) return 1;
    else return f(n-1)+f(n-2);
}

递推版本

int f()
{
   
   
    a[0]=a[1]=0;
    for(int i=2;i<=n;++i) a[i]=a[i-1]+a[i-2];
    return a[n];
}

记忆化搜索

用数组将已经计算过的东西记录下来在下一次使用的时直接用已经计算出的值，避免重复计算，去掉重复的搜索树。

int cal(int n)
{
   
   
    if(f[n]!=0) return f[n];
    return (f[n]=cal(n-1)+cal(n-2));
}

递归之所以慢是因为重复的子树太多。
动态规划方法概要

构造一个公式(递推式)，表示一个问题的解是它的子问题的解相关的公式。自底向上(递推)或者自顶向下(记忆化搜索)的方法。原理就是加法原理，乘法原理，例如最短路问题中有向无环图求单源最短路。

动态规划的定义就是解决多阶段决策过程最优化问题的一种方法。
状态:某一阶段的出发位置称为状态，通常一个阶段包含若干状态。
决策:从某阶段的一个状态演变到下一个阶段某状态的选择。
策略:由开始到终点的全过程中，由每段决策序列称为全过程策略。
状态转移方程:前一阶段的终点就是后一个阶段的起点，由前一阶段的决策选择导出后一阶段的状态，这种关系由 $i$ 阶段到 $i + 1$ 阶段状态的演变规律。

动态规划适用的基本条件

第一必须 具有相同的子问题。
将问题分解成若干子问题，再将这些子问题解决。
子问题做为一个新的问题，也能分解成相同的子问题进行求解。
假设一个问题分解成了 $A$ 、 $B$ 、 $C$ 三个部分，那么 $A$ 、 $B$ 、 $C$ 也能被分解成 $A$ 、 $B$ 、 $C$ 三部分，不是其余
第二 满足最优子结构。
问题的最优解包含着它的子问题的最优解。就是不管前面的策略是什么，此后的决策必须基于当前状态(由上一次次决策产生的最优决策)。
第三 满足无后效性
"过去的步骤只能通过当前的状态影响未来的发展，当前的状态是历史的总结。"说明动态规划只适用于解决当前决策与过去状态无关的问题。状态出现在策略任何一个位置，它的地位相同，都可以实施同样的策略。(无后效性的内涵)。如果当前问题的具体决策，会对解决其它未来的问题产生影响，如果产生了影响，就无法保证决策的最优性。

解决动态规划问题的步骤

1.确定状态:首先分析原问题和子问题。(一维不全就二维，二维不全就三维、四维等等)
状态参数一般是:
(1)描述位置:前（后） $i$ 单位，第 $i$ 列第 $j$ 单位，坐标为 $(i, j)$ 等。
(2)描述数量:取 $i$ 个，不超过 $i$ 个，至少 $i$ 个等。
(3)描述对前后有影响的:状态压缩或一些特殊的性质。
2.确定转移方程
(1)检查参数是否足够。
(2)分情况:最后一次操作的方式、取不取，怎么样放，前一项是什么。
(3)初始边界是什么。
(4)注意无后效性。例:求 $A$ 要求 $B$ ，求 $B$ 要求 $C$ ，求 $C$ 要求 $A$ ，不符合无后效性。
3.确定编程实现方式
(1)递推
(2)记忆化搜索

Max Sum

Max Sum
题目大意
给出一个长度为 $n$ 的数组，数组中每个数据的范围在 -1000 和 1000 之间，求出这个数组最大的连续区间和。
输入格式
第一行输入一个 T，表示有 T 组数据。每个数据的开始为一个整数 $n$ ，表示数组的长度。接下来有 $n$ 个数，表示这个数组的 $n$ 个数。
输出格式
每组数据，输出最大连续区间和，并输出这个连续区间的开始和结束的位置。
样例输入

2
5 6 -1 5 4 -7
7 0 6 -1 1 -6 7 -5

样例输出

Case 1:14 1 4
Case 2:7 1 6

1.确定状态，考虑连续区间，如果 $d p [i - 1] + a [i] > a [i]$ ，更新 $d p [i] = d p [i - 1] + a [i]$ ，区间结束位置肯定在 $d p [i] + a [i + 1] < d p [i]$ 。
2.状态转移方程 $d p [i] = ma x (d p [i] + a [i], d p [i])$

#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int maxn=1e5+7;
int dp[maxn],a[maxn];
int main()
{
   
   
    int T,cs=0;
    scanf("%d",&T);
    int f=T;
    while(T--)
    {
   
   
        memset(dp,0,sizeof dp);
        int n,s,e,pos,maxx=-1010;
        scanf("%d",&n);
        for(int i=1;i<=n;++i) scanf("%d",&a[i]);
        for(int i=1;i<=n;++i)
        {
   
   
            if(dp[i-1]+a[i]>a[i]) dp[i]=dp[i-1]+a[i];
            else dp[i]=a[i],pos=i;
            if(dp[i]>maxx)
            {
   
   
                s=pos;
                e=i;
                maxx=dp[i];
            }
        }
        printf("Case %d:\n%d %d %d\n",++cs,maxx,s,e);
        if(cs<f)puts("");
    }
    return 0;
}

数塔

数塔
题目大意
在讲述DP算法的时候，一个经典的例子就是数塔问题，它是这样描述的：
有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？
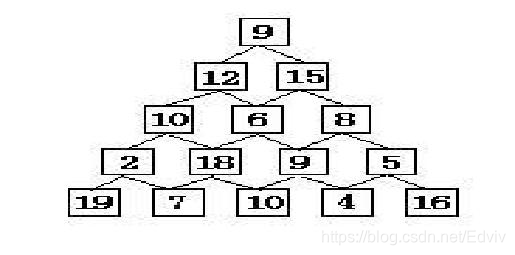
在这里插入图片描述
已经告诉你了，这是个DP的题目，你能AC吗?
输入描述
输入数据首先包括一个整数C,表示测试实例的个数，每个测试实例的第一行是一个整数N(1 <= N <= 100)，表示数塔的高度，接下来用N行数字表示数塔，其中第i行有个i个整数，且所有的整数均在区间[0,99]内。
输出描述
对于每个测试实例，输出可能得到的最大和，每个实例的输出占一行。
输入样例

输出样例

#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=110;
int dp[maxn][maxn],a[maxn][maxn];
int main()
{
   
   
    int t,n;
    scanf("%d",&t);
    while(t--)
    {
   
   
        scanf(" %d",&n);
        for(int i=1;i<=n;++i)
            for(int j=1;j<=i;++j) scanf(" %d",&a[i][j]);

        for(int i=1;i<=n;++i)
            for(int j=1;j<=i+1;++j) dp[i][j]=-0x3f3f3f3f;
        dp[1][1]=a[1][1];
        for(int i=2;i<=n;++i)
            for(int j=1;j<=i;++j)
                dp[i][j]=max(dp[i-1