数据结构与算法之树简介

1.示例树的图示

 

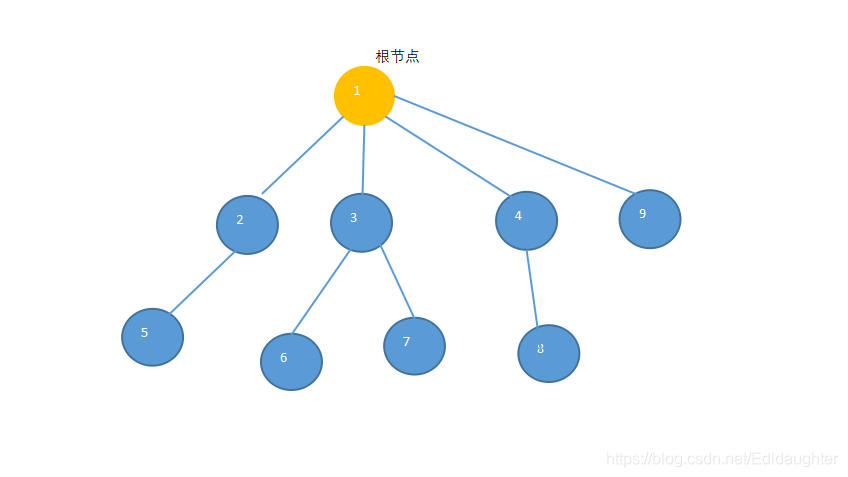
2.树的定义与结构特点

1.树的定义
由一个或者多个(n>=0)节点组成的有限集合T，有且仅有一个节点称为根(root)，当n>1的时候，
其余的节点分为m(m>=0)个互不相交的有限集合T1，T2，...,Tm.每个集合本身又是棵树，被称作这颗树的子树.
(由此可以看出树具有递归性，大树里面有小树).

2.树的结构特点
(1)非线性结构，有一个直接前驱，但可能有多个直接后继（1：n);
(2)树的定义具有递归性，树中还有树；
(3)树可以为空，即节点个数为0；

3.树的 一些术语

根：即根结点，没有前驱；
叶子：即终端结点，没有后继（示例树种的5，6，7，8，9对应的节点）；
森林：指m颗不相交的树的集合（如删除根节点后的子树组成的集合）；
有序树：节点各子树从左到右有序，不能互换（左为第一）；
无序树：节点各子树可以互换位置；
双亲：即上层的那个结点（直接前驱）,称作parent;
孩子：即下层节点的子树（直接后继），称作child;
兄弟：同一双亲下的共层节点（孩子之间互称兄弟），称作sibling;
堂兄弟：即双亲位于同一层但非同一双亲的结点，称作cousin;
祖先：从根结点到该结点索经分支的所有结点；
子孙：该结点下层子树中的任一结点；
结点:即树的数据元素；
结点的度：结点挂接的子树数，有几个直接后继就是几度；
结点的层次：从根到该结点的层数，根基点算第一层；
终端结点：即度为0的结点，即叶子结点；
分支结点:除舒更意外的结点，也称作内部结点；
树的度：所有结点度中的最大值（即MAX(各结点的度))；
树的深度(或高度)：所有结点中最大的层数（即MAX(各结点的层次)）；

4.树的表示方法

图形表示法；
广义表示法；
双亲表示法；
孩子表示法；
左孩子右兄弟表示法(任何一种颗都可以通过左孩子右兄弟表示法转换成一颗二叉树).

5. 利用左孩子右兄弟表示法将一棵树转换

 

 

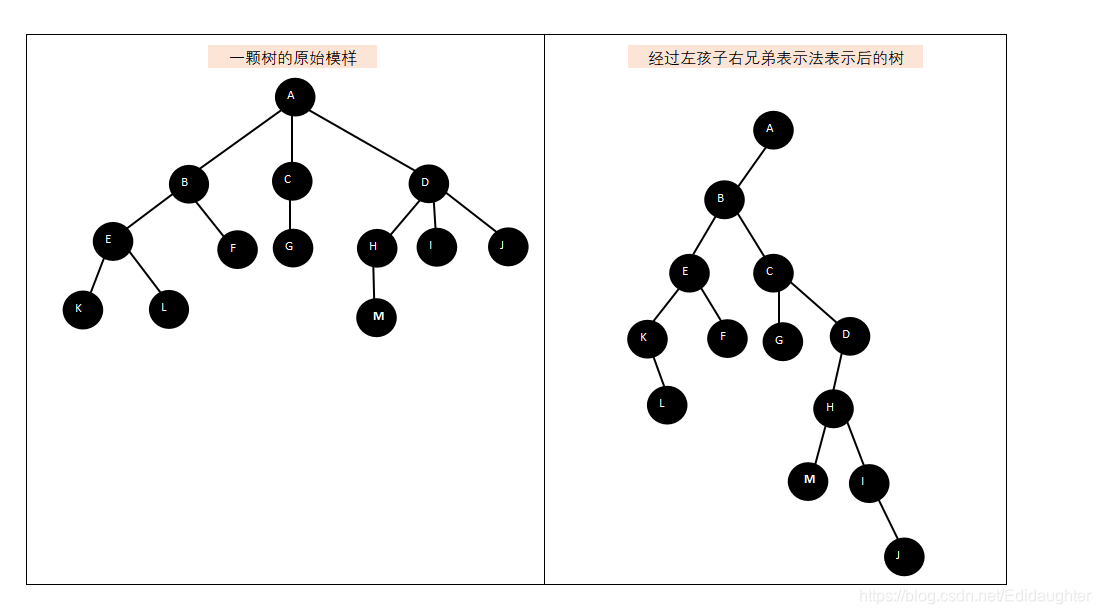
6.二叉树

6.1 二叉树的基本概念

定义：
n(n>=0)个结点的有限集合，有一个根节点以及两颗互不相交的分别称为左子树和右子树的二叉树组成.

逻辑结构：
一对二

基本特征：
每个节点最多只有两颗子树(不存在度大于2的结点)；
左子树和右子树的次序不能颠倒(有序树)；

6.2二叉树的基本形态

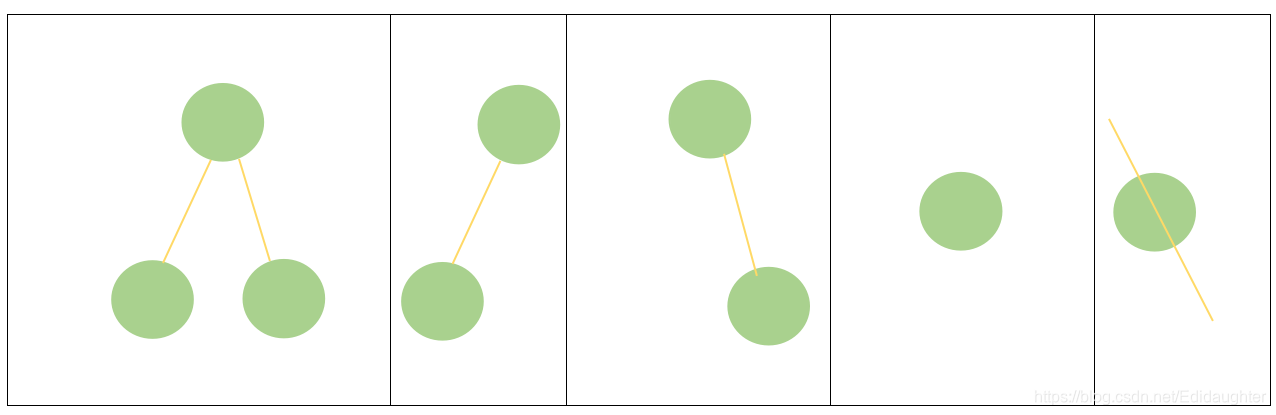
6.3 二叉树的性质

 6.4 特殊的二叉树-满二叉树

定义：
一颗深度为k且有2^k-1个结点的二叉树，每一层都充满了结点.
如下图中的满二叉树的深度为3，则它拥有2^3-1个结点，即7个结点.

 

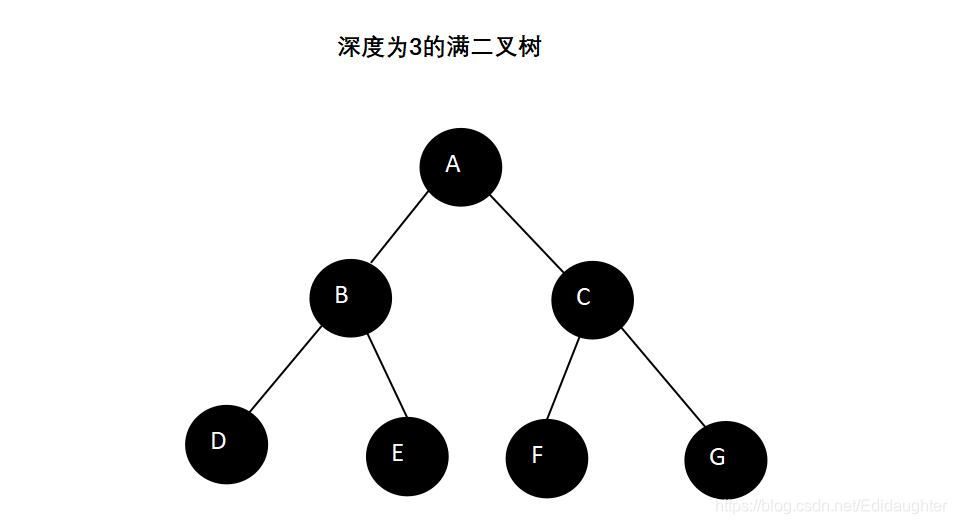
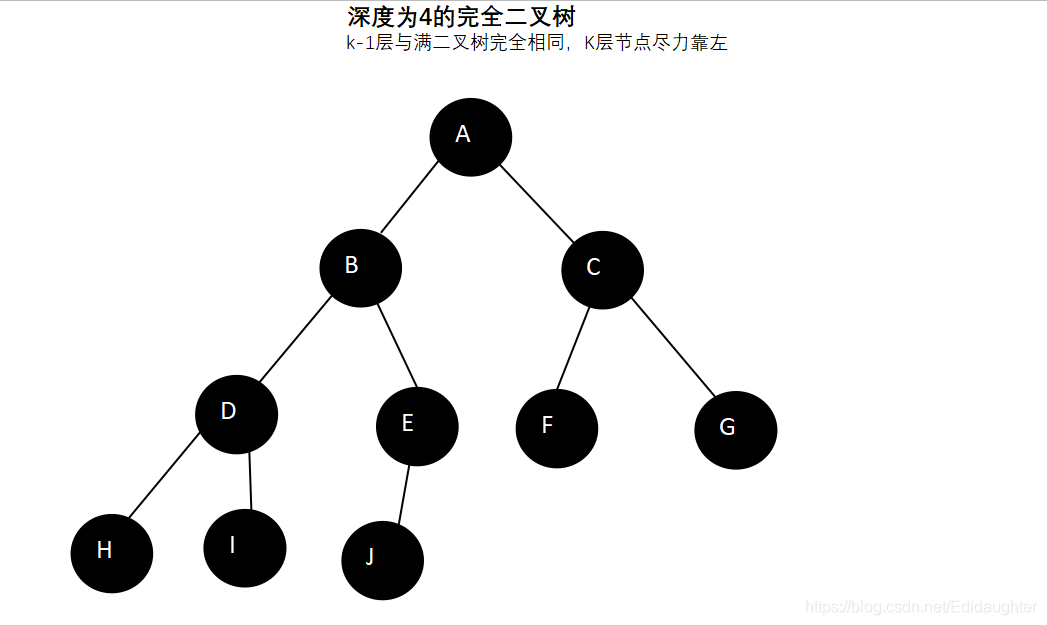
6.5 特殊的二叉树-完全二叉树

定义：
除了最后一层外，每一层上的节点数均达到最大值，在最后一层上只缺少右边的若干节点.

 

 

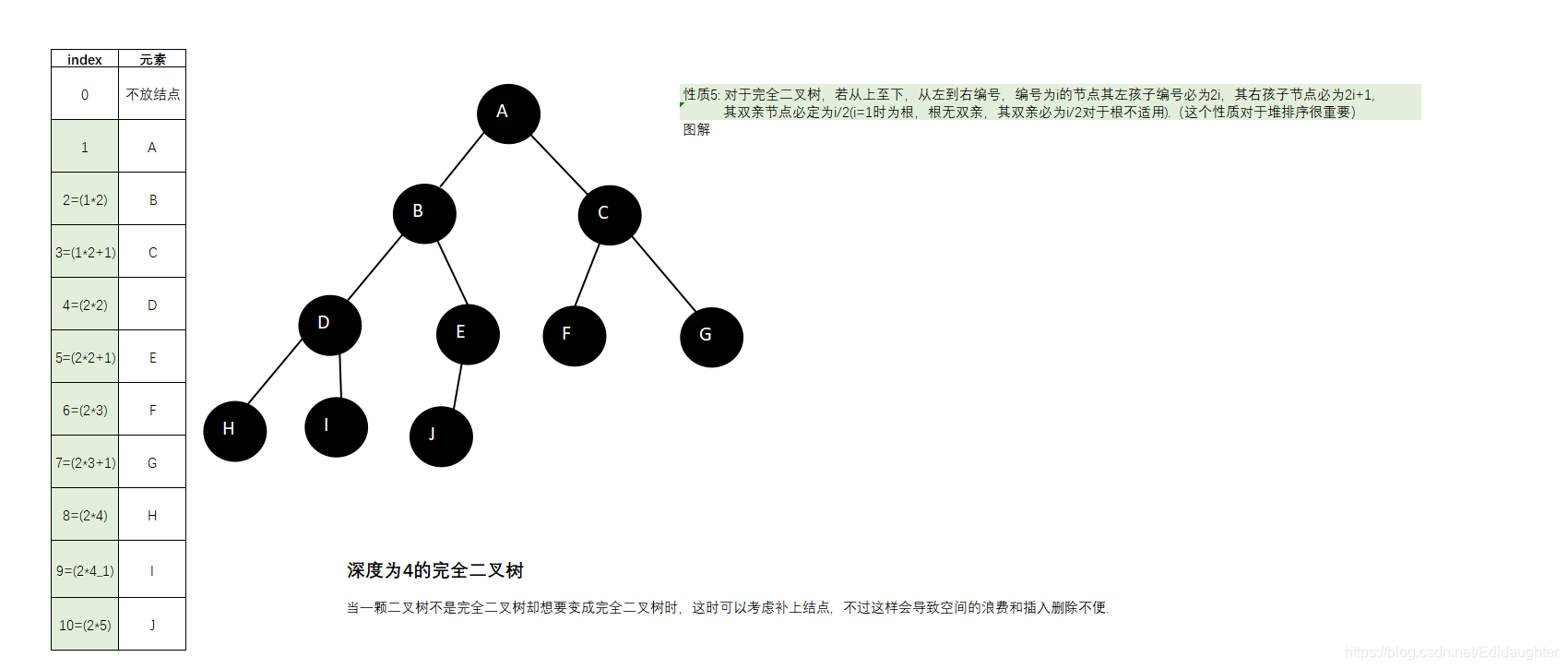
6.6 二叉树性质5的图解释

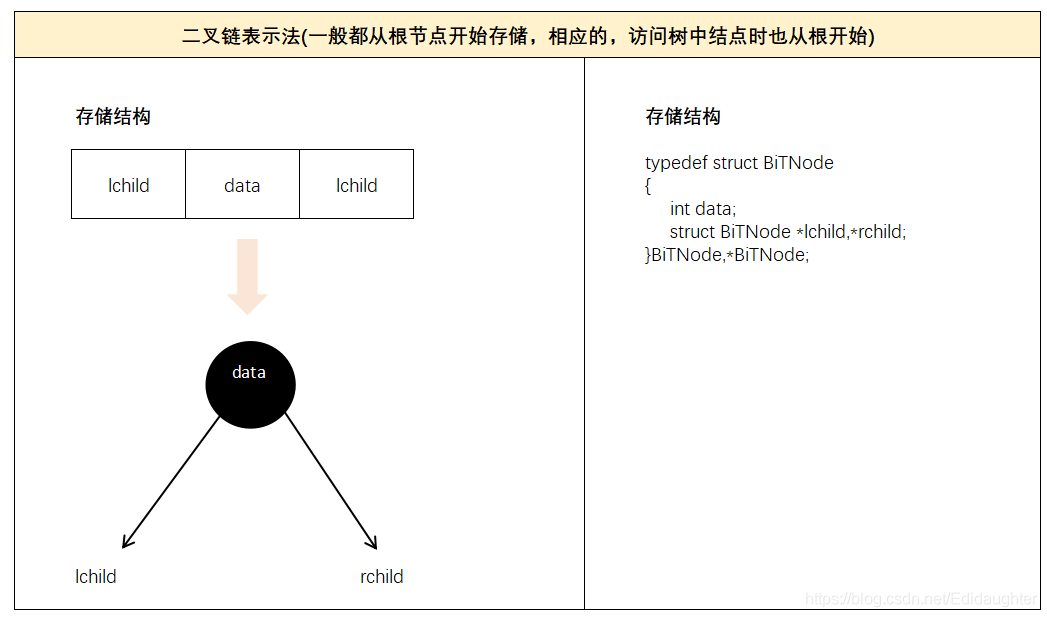
 6.7二叉树的表示

有二叉链表法和三叉链表法

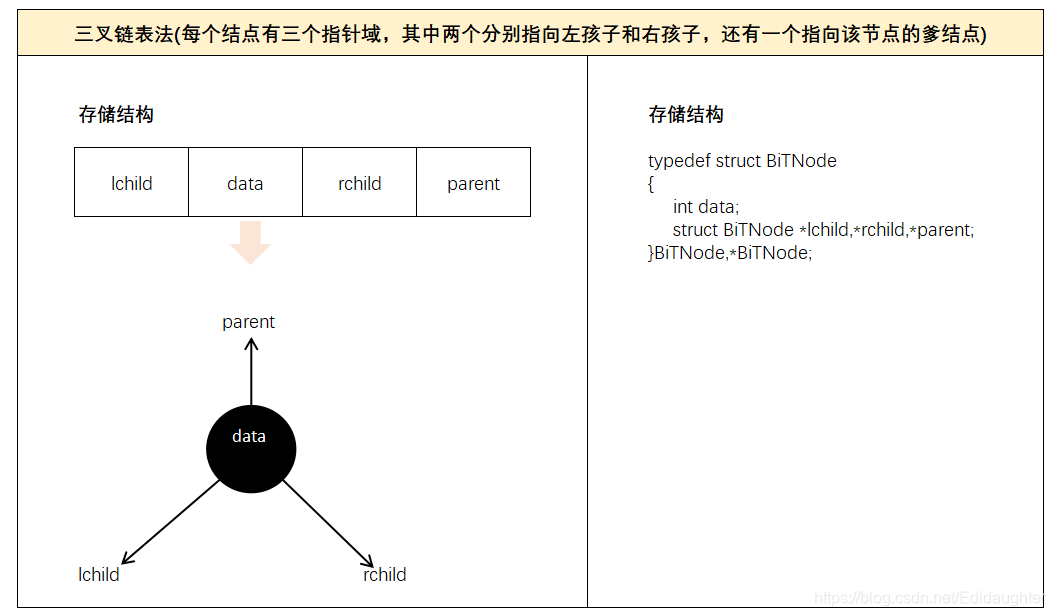
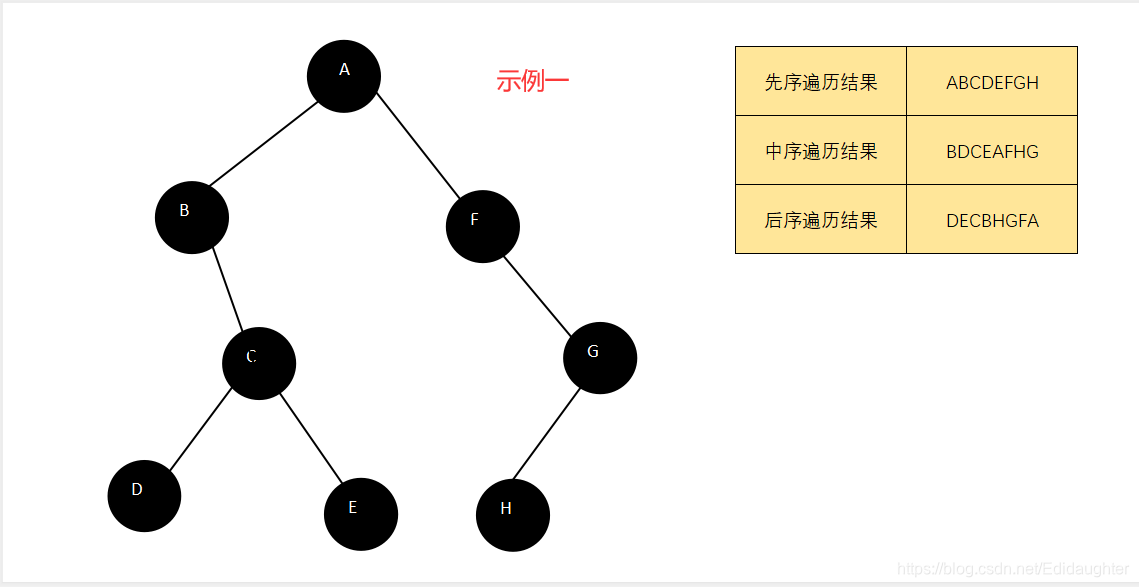
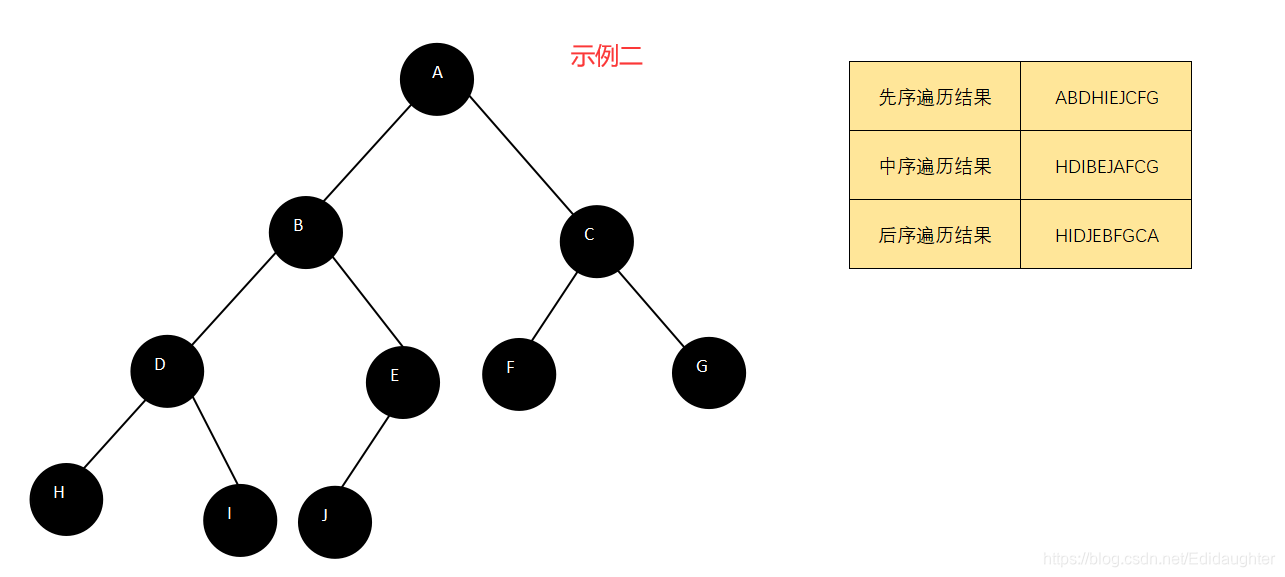
6.8 二叉树的遍历

遍历的定义：
指的是按照某条搜索路线遍访每个结点且不重复(又称周游)；

遍历的用途：
它是树结构插入删除修改查找和排序运算的前提，是二叉树一切运算的基础和核心.

遍历方法：
牢记一种约定，对于每个结点的查考都是“先左后右”.
限定先左后右之后，树的遍历有三种实现方案：
DLR---先根序遍历,先序遍历，即先根再左再右； 
LDR---中根序遍历,中序遍历，即先左再跟再右；
LRD---后根序遍历,后许遍历，即先左再右再根.

注意：这里的先序，中序和后序都是指访问结点D是先于左右子树遍历还是在左右子树中间遍历还是在左右子树后面遍历.
从递归角度来看，这三种算法是完全相同的，或者说这三种遍历算法的路径是相同的，只是访问节点的时机不同.