C语言经典例题100道

程序【11】

题目：古典问题（兔子生崽）：有一对兔子，从出生后第3个月起每个月都生一对兔子，小兔子长到第三个月后每个月又生一对兔子，假如兔子都不死，问每个月的兔子总数为多少？（输出前40个月即可）

程序分析：兔子的规律为数列1,1,2,3,5,8,13,21....，即下个月是上两个月之和（从第三个月开始）。

首先，我们看到了这个古典问题的题目，我们必须去认认真真的读题，发掘出古典问题里更深入的问题。

什么是“古典问题”呢，古典问题就是在古老的时候，人们发现出一些有趣的现象，并且把这种现象用一种古代数学的思想来解答出来。在时代逐渐演变的现在，这些问题仍然很经典，受人们关注，所以，为了更好的研究它们，我们将其称为“古典问题”。

而在时代的发展里，大多数古典问题，也被赋予了新的名字，被赋予新的使命！

当我们看到这题的时候，我们首先要好好的去读题，再根据联想，最后得出一种算法思维，解决问题。

首先，我们先观察题目，初始的兔子，到第三个月的时候才会诞生一对兔子，那么我们就可以知道，在前两个月之前只有一对兔子，当在第三个月的时候，就开始增加兔子的对数，变成两对兔子，这样我们就完全可以找到一种规律--------

1       1         2        3       5       8      13       21       34         55         89   

在这里，我们能够不难的看出来，这就是我们所熟悉的斐波那契数列。

和我上面所说的一样，过去的不死神兔古典问题，就是现在的斐波那契数列！

一个问题，间接表现出两个问题的方法，真不错。

 既然是写斐波那契数列的话，在这里，我将会用多种方法，解决问题。

第一种:非常简单的方法(值传递)

就是类似1+1=2，把后得到的结果2传递给前面的1，占用1的位置

#include<stdio.h>
int main()
{
	long f1 = 0;//第一月的兔子
	int f2 = 0;//第二月的兔子
	int i = 0;//月份循环变量
	f1 = f2 = 1;//前两月都只是一对兔子
	for (i = 1; i <= 20; i++)
	{
		printf("%12ld %12ld", f1, f2);
		if (i % 2 == 0) printf("\n");/*控制输出，每行四个*/
		f1 = f1 + f2; /*前两个月加起来赋值给第三个月*/
		f2 = f1 + f2; /*前两个月加起来赋值给第三个月*/
	}
}

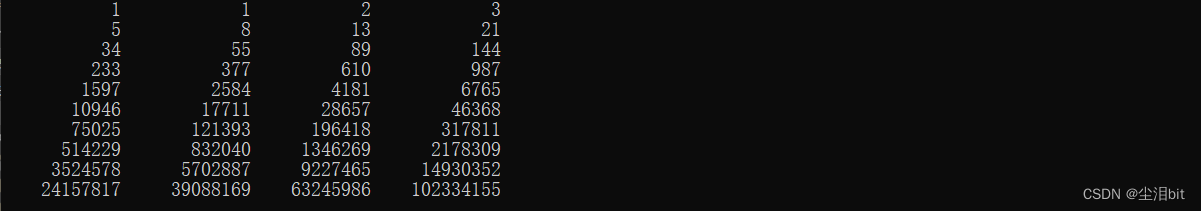第二种:普通的方法(值交换) 

#include<stdio.h>
//有一对兔子，从出生后第 3 个月起每个月都生一对兔子，小兔子长到第三个月
//后每个月又生一对兔子，假如兔子都不死，问每个月的兔子总数为多少？
//---------------------------------------------------------------本质就是斐波那契数列
//1对 1对 2对 3对 5对 8对 13对 21对
//普通的方法：
int main() {
	int i = 1;//声明定义第一个数，下面为前一个数
	int j = 1;//声明定义第二个数，下面为后一个数
	int n = 1;//声明定义月数
	int sum = 0;//声明定义兔子的对数
	for (n = 1; n <= 2; n++)//第一个月第二个月都是1对兔子
	{
		printf("第%d月共有%d对兔子总计%d只兔子", n, 1, 2);
		printf("\n");
	}
	for (n = 3; n<25; n++) //当在第三个月时每个月的兔子都会增加
	{
		sum = i + j;
		i = j;
		j = sum;
		printf("第%d月共有%d对兔子总计%d只兔子", n, sum, sum * 2);
		printf("\n");	
	}
	return 0;
}

 

第三种:运用函数递归的方法(函数调用函数)

函数调用函数的方法

int Fib(int n)//声明并定义函数
{
	if (n == 1 || n == 2) {
		return 1;
	}
	else {
		return Fib(n - 1) + Fib(n - 2);//函数递归
		//函数调用函数
	}
}
#include<stdio.h>
//1 1 2 3 5 8 13 21 34
int main() {
	int n = 0;//表示月份
	int ret = 0;//接收函数的返回值
	for (n = 1; n < 25; n++) {
		ret = Fib(n);
		printf("第%d个月有%d对兔子共有%d只兔子\n", n, ret, 2 * ret);
	}
	return 0;
}

 

特别提醒:------

每个方法都有每个方法的优点和缺点，一般的方法能够更好的理解，但是代码较为麻烦，写编程，最重要的就是理解，理解了代码底层的深度意义，万变不离其宗，题目无论怎么变化，我们都可以很轻松的解答出来。而递归的方法，虽然很简便，但是对于那些不理解递归的小白来说，还不如一般的方法，所以我们应该择优而选，在写编程的时候，做到最优解。其次，递归的方法，相对其他的方法，非常的耗费时间，在某些题目里限制时间是1s，那么递归的方法就不再适用，还是那句话，编程的学习，理解最为重要！！！