机器学习笔记1【算法分类&单变量线性回归】

1机器学习算法的分类

1.1 监督学习

• 回归问题。 一般数处理连续值，比如提到的房屋售价预测
• 分类问题。 一般事处理离散值，比如判断肿瘤是良性还是恶性

1.2 无监督学习

• 聚类问题 。将收集到的新闻分成不同的专题，事先不知道有哪些专题

2 单变量线性回归

2.1 模型描述

1. 常用的符号语言，

   • m代表训练样本的数量
   • x输入变量，属性
   • y输出变量，结果
   • (x,y)一个训练样本
   • (x^i,y^i)第i个训练样本

2. 机器学习算法的目的，是通过训练数据集得到一个假设函数h（hypothesis）$h(x)={\theta }_0+{\theta }_{1}x$，这个h的作用是，输入一个x可以得到一个输出变量y

2.2 代价函数

1. 代价函数（cost function）在单变量线性回归中一般选择平方误差函数（square error function）：

$$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=0}^m(h(x^{(i)})-y^{(i)})\text{\hspace{1em}(2.1)}$$
需要做的是找到使$J({\theta }_0,{\theta }_1)$最小的${\theta }_0,{\theta }_1$

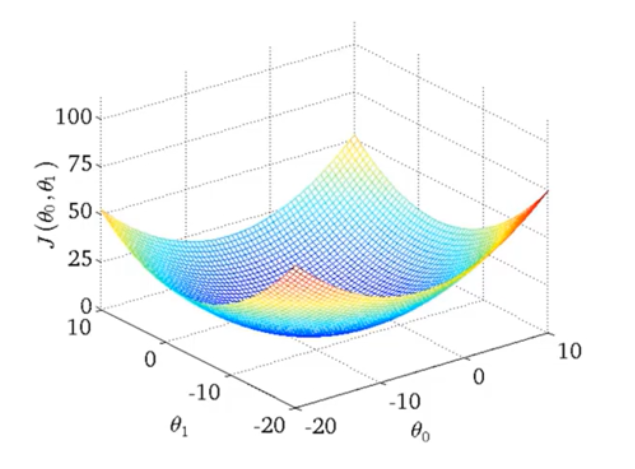
2. 代价函数中的一个点，代表了一组${\theta }_0,{\theta }_1$的取值，即一个假设函数$h$

2.3 梯度下降

1. 梯度下降是一种最小化代价函数的方法，不仅适用于平方误差函数
2. 思想是：先任取一组${\theta }_0,{\theta }_1$的值，然后不断改变${\theta }_0,{\theta }_1$的值来减少$J({\theta }_0,{\theta }_1)$，直到$J$的最小值（或者极小值）
3. 表达式：
   (3.1) r e p e a t   u n t i l   c o n v e r g e n c e { θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) ( f o r   j = 0   a n d   j = 1 ) } repeat\ until\ convergence\{ \\ \quad \theta_j := \theta_j - \alpha \frac{\partial}{\partial {\theta_j}} J(\theta_0,\theta_1) \quad (for\ j = 0 \ and\ j = 1) \tag{3.1} \\ \} repeat until convergence{θj​:=θj​−α∂θj​∂​J(θ0​,θ1​)(for j=0 and j=1)}(3.1)
4. 具体的计算过程：
   

2.4其他需要注意的

1. • :=是赋值的意思

   • 每次计算必须同时更新${\theta }_0,{\theta }_1$，即更新顺序为
     $$\begin{gathered} temp0:={\theta }_0:={\theta }_0-\alpha \frac{\partial }{\partial {\theta }_0}J({\theta }_0,{\theta }_1) \\ temp1:={\theta }_1:={\theta }_1-\alpha \frac{\partial }{\partial {\theta }_1}J({\theta }_0,{\theta }_1) \\ {\theta }_0:=temp0 \\ {\theta }_1:=temp1\text{\hspace{1em}(3.2)} \end{gathered}$$

   • $\alpha$是学习效率（learning rate），决定着${\theta }_0,{\theta }_1$的更新速度，$\alpha$太小可能收敛速度会很慢，$\alpha$太大可能导致不收敛或者发散

2. 梯度下降的直观理解：
   以只考虑一个变量${\theta }_1$为例，
   [外链图片转存失败(img-9u86zUha-1563951056546)(.\images\1.png)]
   粉红色的点为初始点为初始点，在该点求出对${\theta }_1$的导数（不是偏导是因为在这里只考虑一个变量），乘以学习效率 $\alpha$，更新${\theta }_1$得到绿色的第二个点，重复这个步骤，直到到达最低点。
   需要明确的是，在上述迭代过程中不需要更新$\alpha$，因为$(3.1)$中的偏导数（导数部分）会随着${\theta }_0,{\theta }_1$接近局部最低值而减小

3. 有时候也称为批量梯度下降法（batch gradient descent），因为在梯度下降的每一步中，我们都用到了所有的训练样本。

4. 梯度下降法有时候会局限于局部最优解，但是绝大部分时候，代价函数都是一个弓形函数，即凸函数，只有一个全局最优解，所以不用担心。