2019-2024元启发式算法TOP23：原理、改进与实际应用

本文系统梳理了2019至2024年间最具影响力的23种元启发式算法，基于引文影响力、求解效能、跨领域适应性等筛选标准，重点介绍了哈里斯鹰优化算法（HHO）、蝴蝶优化算法（BOA）、基于梯度的优化器（GBO）等算法的原理、数学模型、改进变体（如hHHO-SCA、DBOA）及其在工程设计、机器学习、能源调度等领域的应用案例，揭示了算法在探索-开发平衡、局部最优管理等关键技术上的创新，并展望其未来广泛应用前景。

最具影响力的元启发式算法（2019-2024年间）

本节将全面概述2019至2024年间开发的元启发式算法最新进展，展示其前沿应用的关键案例。我们的筛选标准包括引文影响力、求解效能、跨领域适应性，以及探索-开发技术创新和局部最优管理机制。我们预计这些元启发式算法将在未来几年获得更高关注度并得到更广泛应用，从而区别于该领域其他近期算法。

元启发式算法	年份	被引次数
哈里斯鹰优化算法（Heidari等，2019）	2019	11300
蝴蝶优化算法（Arora & Singh，2019）	2019	6150
基于梯度的优化器（Ahmadianfar等，2020）	2020	5990
粘菌算法（Li等，2020）	2020	5570
海洋捕食者算法（Faramarzi等，2020a）	2020	5080
平衡优化器（Faramarzi等，2020b）	2020	4890
天鹰优化器（Abualigah等，2021）	2021	3300
海鸥优化算法（Dhiman & Kumar，2019）	2019	3050
蝠鲼觅食优化算法（Zhao等，2020b）	2020	2990
黑猩猩优化算法（Khishe & Mosavi，2020）	2020	2420
松鼠搜索算法（Jain等，2019）	2019	2280
亨利气体溶解度优化算法（Hashim等，2019）	2019	2150
阿基米德优化算法（Hashim等，2021）	2021	2080
被囊群算法（Kaur等，2020）	2020	2020
蜜獾算法（Hashim等，2022）	2022	1970
蜉蝣优化算法（Zervoudakis & Tsafarakis，2020a）	2020	1720
非洲秃鹫优化算法（Abdollahzadeh等，2021a）	2021	1250
金豺优化算法（Chopra & Ansari，2022）	2022	985
蜣螂优化器（Xue & Shen，2023）	2023	966
浣熊优化算法（Dehghani等，2023a）	2023	769
混沌博弈优化算法（Oueslati等，2024）	2024	767
白鲸优化算法（Zhong等，2022）	2022	710
瞪羚优化算法（Agushaka等，2023）	2023	442

3.1. 哈里斯鹰优化算法

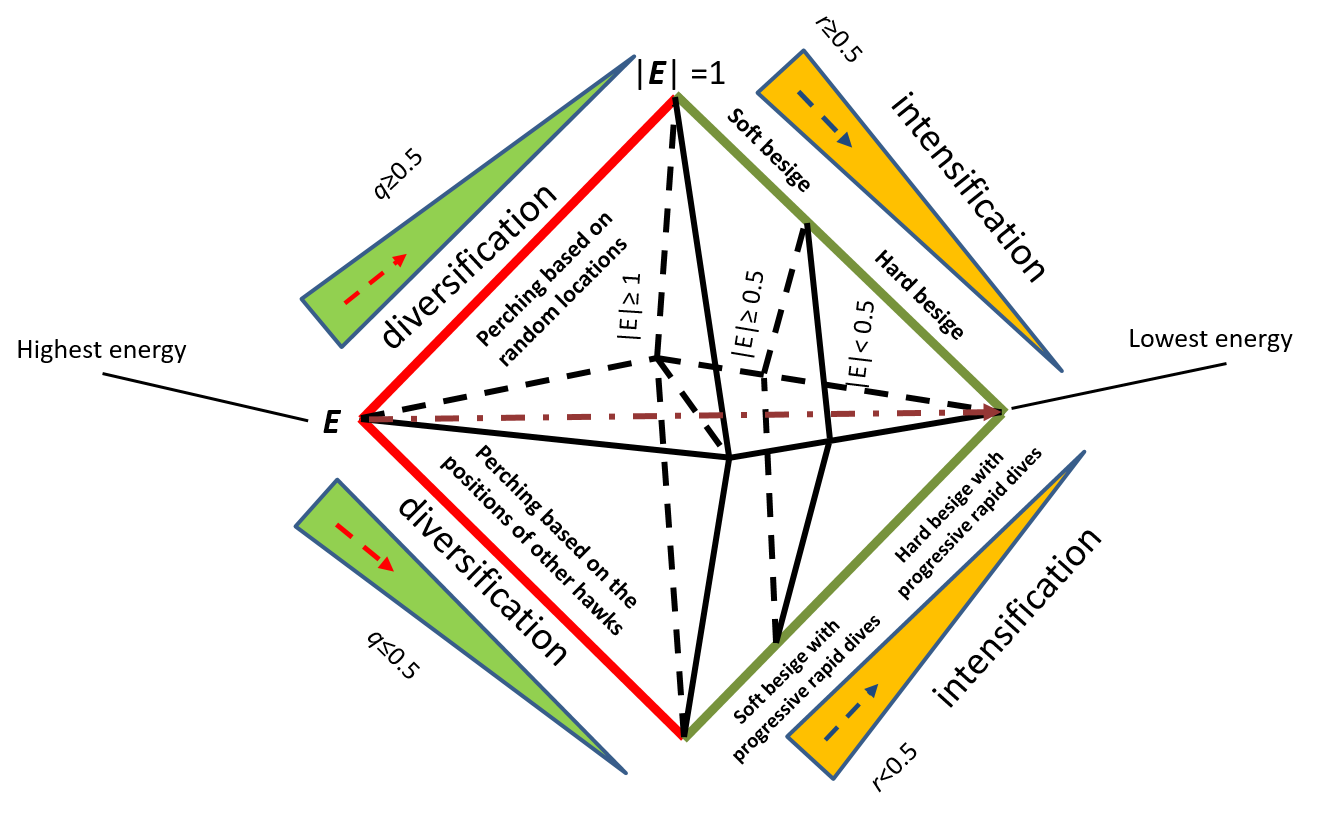
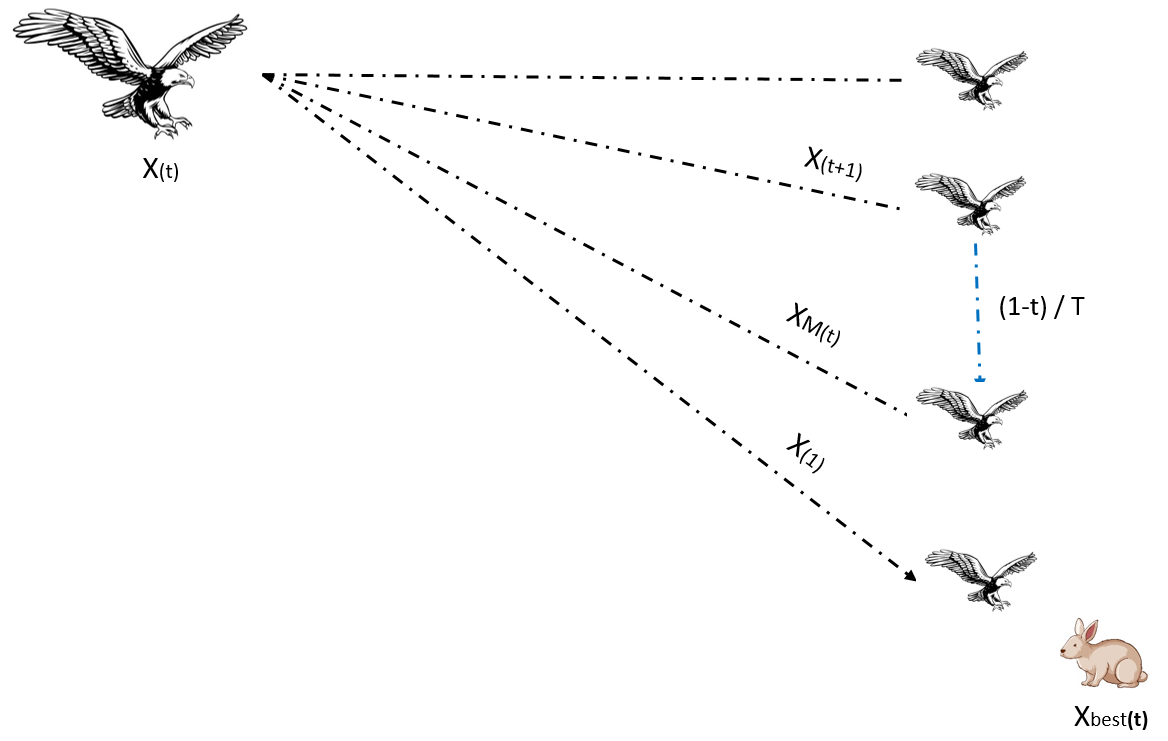
哈里斯鹰优化算法（Harris Hawk Optimization，HHO）是一种受哈里斯鹰合作捕猎策略启发的高效元启发式算法。哈里斯鹰以群体战术和对猎物的突然袭击著称（Heidari等，2019；Alabool等，2021）。HHO算法在解决具有非线性、高维度和多局部最优特征的复杂优化问题中表现尤为突出。HHO模拟鹰类侦察猎物并执行协同突袭的过程，实现解空间的探索（广泛搜索）与开发（局部搜索）。根据能量水平（E）、q和r值的HHO步骤如图2所示。

HHO从随机初始化的候选解种群开始，通过模拟真实鹰类捕猎的动态行为对解进行评估和迭代更新。在探索阶段，算法进行广泛搜索以避免局部最优；若识别到有潜力区域，则进入开发阶段，此时鹰类执行策略性突袭以快速收敛到高质量解。这些动作受模拟猎物逃逸模式的自适应参数影响，有助于平衡全局搜索与局部搜索。

初始化由以下公式表示的N只鹰的种群：

$$X_i=\left(x_{i,1},x_{i,2},\cdots ,x_{i,d}\right)i=1,2,\cdots ,N\text{\hspace{1em}(1)}$$

其中d为搜索空间的维度。鹰的位置在问题边界内随机初始化。在探索阶段，鹰类基于当前位置和参考领导者（当前找到的最优解）随机搜索猎物：

$$X_i(t+1)=X_{\text{rand}}(t)-r_1\left|X_{\text{rand}}(t)-2r_2{X}_i(t)\right|,\text{\hspace{1em}(2)}$$

其中Xrand为随机选择的鹰，r₁和r₂为[0,1]区间内的均匀随机数。

从探索到开发的过渡取决于猎物行为和逃逸能量E：

$$E=2E_0\left(1-\frac{t}{T}\right)\text{\hspace{1em}(3)}$$

其中E₀为[-1,1]范围内的随机数，t为当前迭代次数，T为最大迭代次数。

若|E|≥0.5，鹰类执行软包围（开发阶段）：

$$X_i(t+1)=\Delta X(t)-E\left|J{X}_{\text{best}}(t)-X_i(t)\right|\text{\hspace{1em}(4)}$$

其中ΔX(t)为最优解与当前解的差值，J为随机跳跃强度系数。

若|E|＜0.5，鹰类执行硬包围：

$$X_i(t+1)=X_{\text{best}}(t)-E\left|X_{\text{best}}(t)-X_i(t)\right|.\text{\hspace{1em}(5)}$$

在随机攻击或突袭情况下，鹰类模拟突然俯冲：

$$X_i(t+1)=X_{\text{prey}}(t)-E\left({\left|X_{\text{prey}}(t)-X_i(t)\right|}^{\beta }\right)\text{\hspace{1em}(6)}$$

其中β为模拟突然动作的控制参数。

Kamboj等（2020）通过提出混合变体HHO-正弦余弦算法（hHHO-SCA）增强了全局搜索能力并防止局部最优。该变体将正弦余弦算法（SCA）的探索机制集成到HHO中以提升性能。hHHO-SCA已在复杂、非线性、非凸且高度约束的工程设计问题中测试，结果表明其性能优于标准SCA、HHO及其他优化算法（如蚁狮优化器、飞蛾火焰优化、灰狼优化器）。该算法在多种优化问题中表现出卓越性能，支持其在多学科设计与工程任务中的有效性。Elgamal等（2020）提出的CHHO对标准HHO进行了两项重要改进：一是在初始化阶段应用混沌映射以提高种群多样性，实现更优的搜索空间探索；二是集成模拟退火（SA）以优化当前最优解，增强算法的开发能力。Too等（2019）提出的二次二进制HHO（QBHHO）旨在改善探索-开发平衡，为特征选择提供更优解。BHHHO和QBHHO的有效性通过UCI机器学习库的22个数据集验证。

3.2. 蝴蝶优化算法

蝴蝶优化算法（Butterfly Optimization Algorithm，BOA）是一种基于蝴蝶觅食与交配行为的元启发式算法（Arora & Singh，2019）。它模拟蝴蝶利用嗅觉寻找食物或配偶的过程，平衡搜索空间的探索与开发。BOA已成功应用于各类优化问题，在寻找最优解中表现出竞争力（蝴蝶运动行为如图3所示）。

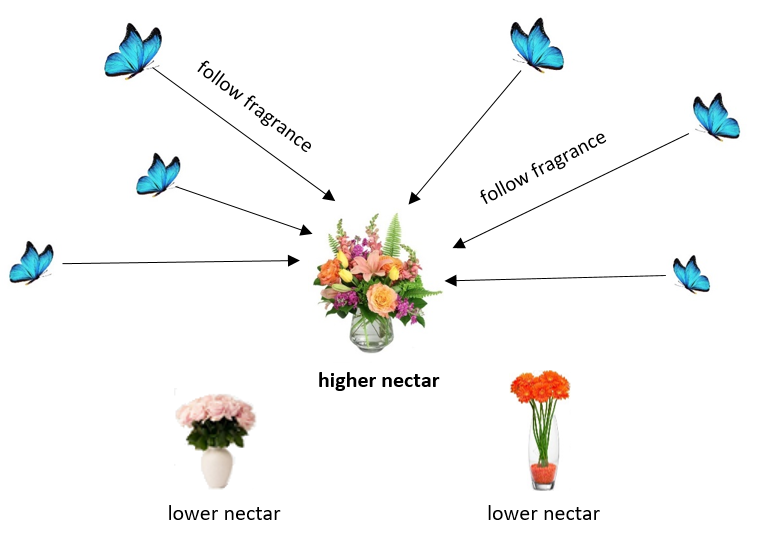
蝴蝶通过感官感知（建模为香味）评估解的质量（适应度）。香味定义为：

$$f_i=c\cdot I_i^a\text{\hspace{1em}(7)}$$

其中fᵢ为蝴蝶i的香味，c为常数，Iᵢ为解的适应度（气味强度），a为感官模式参数，控制感知程度。蝴蝶的运动由全局与局部搜索策略共同控制，具体取决于感知的香味。全局搜索允许蝴蝶向种群中的最优解移动：

$$X_i(t+1)=X_i(t)+r\cdot f_i\cdot \left(X_{\text{best}}-X_i(t)\right)\text{\hspace{1em}(8)}$$

其中Xbest为当前找到的最优解，r为[0,1]随机数，fᵢ为蝴蝶i的香味。局部搜索中，运动由邻近蝴蝶的香味决定：

$$X_i(t+1)=X_i(t)+r\cdot f_i\cdot \left(X_j(t)-X_k(t)\right)\text{\hspace{1em}(9)}$$

其中Xⱼ(t)和Xₖ(t)为随机选择的两只蝴蝶。为切换全局与局部搜索，引入随机切换概率p：

$$p=\text{rand}(0,1)\text{\hspace{1em}(10)}$$

若p小于阈值p₀则执行全局搜索，否则执行局部搜索。该机制确保探索与开发的平衡。感官模式参数a随迭代自适应调整以微调算法：

$$a(t)=a_{\min }+\left(a_{\max }-a_{\min }\right)\cdot \frac{t}{T}\text{\hspace{1em}(11)}$$

其中a_min和a_max定义感官模式范围，t为当前迭代次数，T为总迭代次数。

Tubishat等（2020）提出动态BOA（DBOA），解决其在高维问题中的局部最优停滞与解多样性不足等局限。通过集成基于变异的局部搜索算法（LSAM），DBOA提升了解多样性并避免局部最优。在20个UCI基准数据集上的实验表明，DBOA在多种性能指标上优于其他算法。Makhadmeh等（2023）介绍了BOA的信息以阐明其核心基础与相关优化概念，提供了BOA的灵感来源与数学模型及示例以证明其高能力。随后，所有综述研究按适应形式分为原始、改进和混合三类，并详细解释了BOA的主要应用，分析了其在优化问题中的优缺点，最后总结了未来研究方向。Alweshah等（2022）将帝王BOA（MBO）算法与基于KNN分类器的包装特征选择（FS）方法结合，在18个基准数据集上测试，MBO优于四种元启发式算法（WOASAT、ALO、GA、PSO），平均分类准确率达93%并显著减少特征选择规模，结果证明其在FS中的有效性与高效性，且全局与局部搜索平衡良好。

3.3. 基于梯度的优化器

基于梯度的优化器（Gradient-based Optimizer，GBO）结合了梯度方法与群体方法，搜索方向由牛顿法确定，通过一组向量和两个主要算子（梯度搜索规则与局部逃逸算子）探索搜索域。优化问题中考虑目标函数的最小化（Ahmadianfar等，2020；Daoud等，2023）。基于梯度的优化器通过计算梯度（即函数对模型参数的斜率或变化率），然后沿降低目标函数的方向更新参数，以寻找最优或近似最优解。

最广泛使用的基于梯度的优化器之一是随机梯度下降（Stochastic Gradient Descent，SGD）（Amari，1993），其基于单个或小批量样本计算的梯度更新参数。该方法比全批量梯度下降（Hinton等，2012）更快（尤其对大数据集），但可能存在更新噪声且难以应对复杂优化景观。为解决这些问题，已开发动量、Nesterov加速梯度、Adagrad、RMSprop和Adam（自适应矩估计）等变体。

基于梯度的优化器在深度学习、强化学习和计算机视觉等领域至关重要，其通过聚焦参数空间中逐步降低误差的区域，实现大型模型的高效训练。然而，对梯度的依赖使其易陷入局部极小值或鞍点（尤其在高维非凸问题中）。因此，研究人员持续开发增强方法与替代算法，以提升这些优化器在各类机器学习应用中的鲁棒性。

Premkumar等（2021）提出多目标GBO（MOGBO）以解决多目标桁架设计问题。MOGBO采用基于梯度的方法（含局部逃逸算子与梯度搜索规则），利用非支配排序与拥挤距离机制实现帕累托最优解。在多种基准问题上的性能测试表明，MOGBO在准确率、运行时间及超体积、多样性等指标上优于其他算法，证明其在复杂多目标优化任务中的有效性。Jiang等（2021）提出8种二进制GBO变体，利用S型和V型传递函数将搜索空间转换为离散格式，在18个UCI数据集和10个高维数据集上评估这些二进制GBO算法并与其他特征选择方法比较，结果表明其中一种变体表现最优，在多种指标上展现出更优整体性能。Helmi等（2021）提出新算法（GBOGWO），通过灰狼优化器（GWO）算子增强GBO的特征选择方法，以应对高维数据挑战并提升人类活动识别（HAR）分类性能。利用UCI-HAR和WISDM数据集，GBOGWO平均分类准确率达98%，证明其在优化HAR模型性能中的有效性。

3.4. 黏菌算法

黏菌算法（Slime Mould Algorithm，SMA）主要模拟多头绒泡菌（Physarum polycephalum）觅食过程中的行为与形态变化，而非其整个生命周期（Li等，2020；Chen等，2023）。该生物是一种在寒冷潮湿环境中生存的真核生物，其主要营养阶段为原质团（代表黏菌的活跃动态阶段，也是本综述的重点）。在此阶段，黏菌主动搜索食物、包围食物并释放酶消化。迁移时，前沿扩展为扇形，由相互连接的静脉网络支撑细胞质流动（如图4所示）。因其独特结构与行为，黏菌可同时利用多个食物源，形成连接它们的网络。黏菌的觅食形态如图4所示。

黏菌通过检测空气中的气味定位食物源。为数学建模

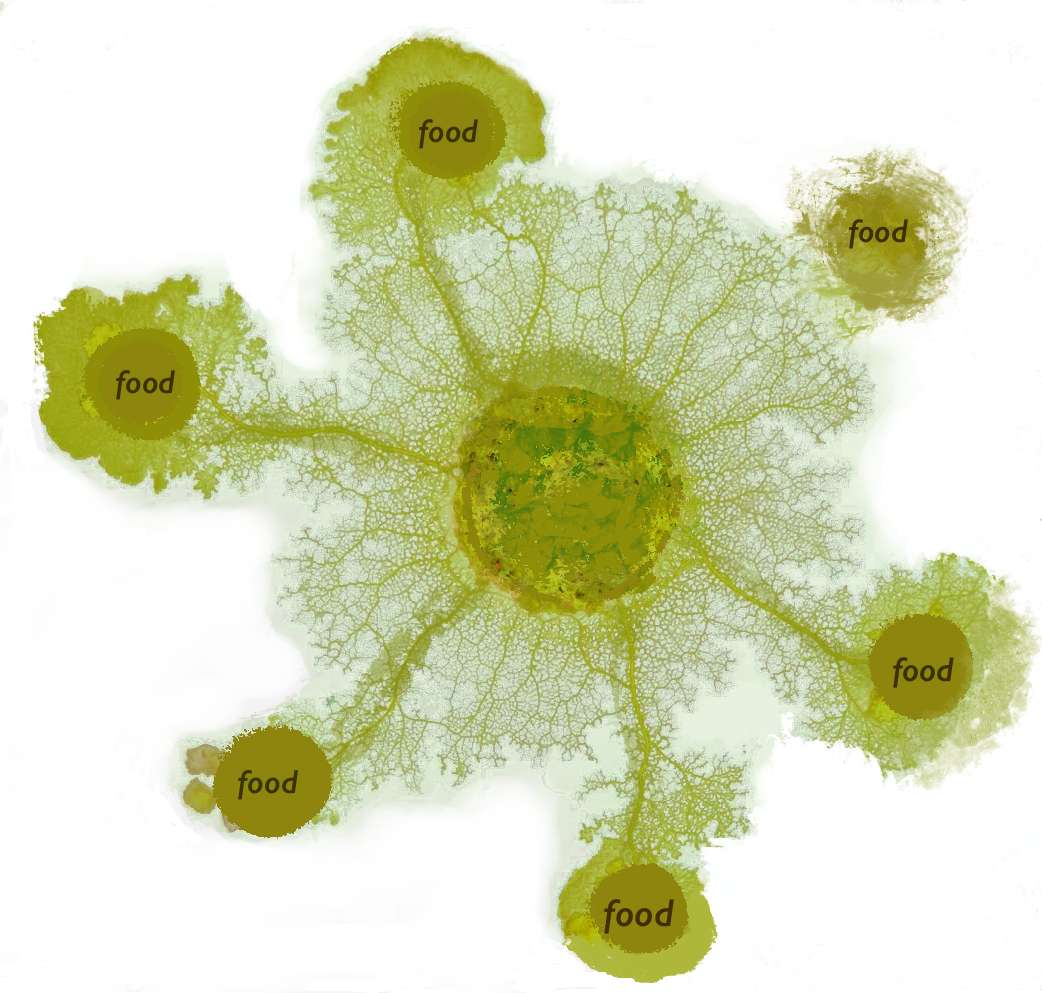
这种觅食行为，提出以下公式模拟收缩模式。黏菌通过检测空气中的气味向食物源移动。为数学表示这种接近行为，提出以下公式模拟收缩模式：

$$X(\overrightarrow{t+1})=\{\begin{array}{ll}\overrightarrow{X_b}(t)+\overrightarrow{vb}\cdot \left(\vec{W}\cdot \left(\overrightarrow{X_A}(t)-\overrightarrow{X_B}(t)\right)\right),& r<p\\ \overrightarrow{vc}\cdot \vec{X}(t),& r\ge p\end{array}$$

其中$\overrightarrow{vb}$为[-a,a]范围内的参数，$\overrightarrow{vc}$从1线性递减至0。变量t表示当前迭代，${\vec{X}}_b$表示检测到气味浓度最高个体的位置，$\vec{X}$表示黏菌位置，${\vec{X}}_A$和${\vec{X}}_B$为从黏菌种群中随机选择的两个个体。此外，$\vec{W}$表示黏菌权重，公式如下：

$$W(\overrightarrow{\text{SmellIndex}}(i))=\{\begin{array}{ll}1+r\cdot \log \left(\frac{bF-S(i)}{bF-wF}+1\right),& \text{condition}\\ 1-r\cdot \log \left(\frac{bF-S(i)}{bF-wF}+1\right),& \text{otherwise}\end{array}$$

其中“条件”表示S(i)在种群前半部分排序，r为[0,1]随机值，bF为当前迭代中获得的最佳适应度值，wF为迭代过程中获得的最差适应度值，SmellIndex为最小化问题中按升序排列的适应度值序列。

搜索个体$\vec{X}$的位置可基于当前识别的最佳位置${\vec{X}}_b$更新，参数${\vec{v}}_b$、${\vec{v}}_c$和$\vec{W}$的调整可修改个体位置。公式中随机变量的引入允许个体在任意角度创建搜索向量，使其能在所有方向探索解空间，从而增强算法寻找最优解的潜力。

下一步是黏菌在搜索过程中静脉组织结构的收缩模式。静脉遇到的食物浓度越高，生物振荡器产生的波越强，导致细胞质流动越快，静脉越粗。公式13从数学上建模了所研究的黏菌静脉宽度与食物浓度之间的正负反馈。公式13中的分量r表示静脉收缩模式中的不确定性。利用对数来调节数值变化速率，确保收缩频率不会过度波动。"条件"反映了黏菌如何根据食物质量调整搜索模式：当食物浓度高时，该区域的权重增加；反之，当食物浓度低时，权重减小，促使黏菌探索新区域。基于上述原理，黏菌位置更新的数学公式如下：

$$\overrightarrow{X^{\ast }}=\{\begin{array}{ll}\text{rand}\cdot (UB-LB)+LB,& \text{if rand}<z\\ \overrightarrow{X_b}(t)+\overrightarrow{vb}\cdot \left(W\cdot \overrightarrow{X_A}(t)-\overrightarrow{X_B}(t)\right),& \text{if }r<p\\ \overrightarrow{vc}\cdot \vec{X}(t),& \text{if }r\ge p\end{array}$$

其中LB和UB分别表示搜索范围的上下边界，rand和r表示区间[0,1]内的随机值，z用于振荡调节。

Chen等人（2023）研究分析了与SMA（黏菌算法）发展相关的关键研究。从Web of Science数据库中检索、筛选并识别了共98项与SMA相关的研究。该综述聚焦于两个主要方面：SMA的改进版本及其应用领域。Premkumar等人（2020）基于实验室实验中黏菌的振荡行为，提出了一种用于解决工业环境中多目标优化问题的多目标黏菌算法（MOSMA）。MOSMA将SMA的核心原理与精英非支配排序和拥挤距离算子相结合，确保帕累托最优解的广泛覆盖。通过41个不同案例研究的测试，MOSMA在多项性能指标上优于现有算法（MOSOS、MOEA/D、MOWCA），展示了其处理复杂多目标优化问题的强大能力。Houssein等人（2022）开发了一种称为MOSMA的多目标SMA，用于解决复杂的多目标优化问题。MOSMA引入外部存档存储和管理帕累托最优解，模拟多目标搜索空间中黏菌的社会行为。通过CEC’20基准测试和各类工程问题验证，MOSMA在解与帕累托集的接近度和反向生成距离方面优于六种成熟算法（如MOGWO、NSGA-II），证明了其在汽车螺旋弹簧优化等实际应用中的优势。

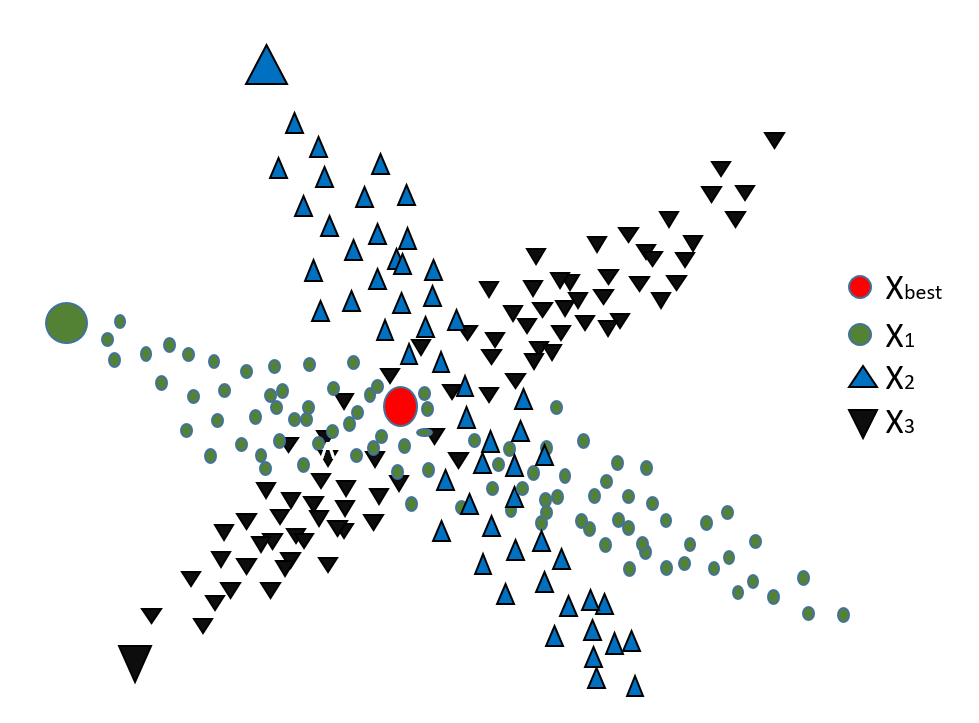
3.5. 海洋捕食者算法

海洋捕食者算法（MPA）模拟了海洋捕食者在海洋中觅食的行为（Faramarzi等，2020a）。该算法主要依赖不同的运动阶段，这些阶段基于捕食者与猎物的相互作用代表了不同的捕食策略。MPA的阶段见图5。

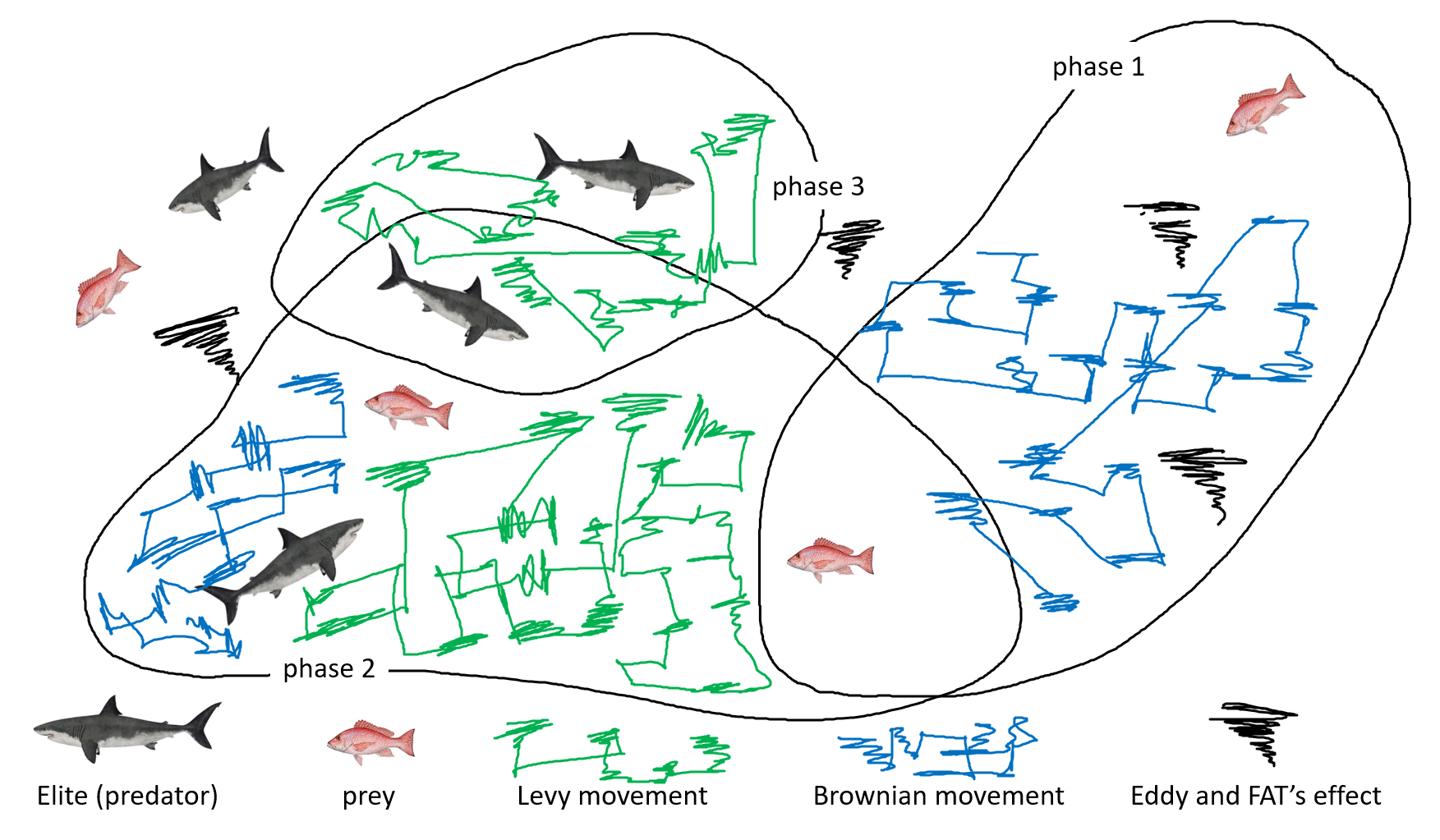
在初始探索阶段，算法采用受莱维飞行启发的随机运动。每个捕食者Xi在迭代t+1时的位置更新如下：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^t+r\cdot \text{Levy}(\lambda )\cdot \left({\mathbf{X}}_i^t-{\mathbf{X}}_{\text{best}}^t\right)$$

其中r是[0,1]范围内的随机数，Levy(λ)表示具有缩放参数λ的莱维飞行，Xbest^t是当前找到的最优解位置。

在开发阶段，若猎物靠近捕食者，则基于"布朗运动"机制调整运动。该阶段的位置更新公式为：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_{\text{best}}^t+B\cdot \left({\mathbf{X}}_i^t-{\mathbf{X}}_{\text{best}}^t\right)$$

其中B表示随机布朗运动。

若猎物较远，算法采用不同的运动策略：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_{\text{best}}^t+F\cdot \left({\mathbf{X}}_i^t-{\mathbf{X}}_{\text{mean}}^t\right)$$

其中F是随机因子，Xmean^t是迭代t时所有解的平均位置。

为模拟猎物逃逸，应用多样化策略：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^t+S\cdot \left({\mathbf{X}}_i^t-{\mathbf{X}}_{\text{worst}}^t\right)$$

其中S是缩放因子，Xworst^t是最差解位置。

Abd Elminaam等人（2021）提出了MPA-KNN，一种MPA与k近邻（k-NN）的新型混合算法，用于改进医疗数据集（特征规模从微小到庞大）的特征选择。实验结果表明，在18个UCI医疗基准数据集上，MPA-KNN在准确率、灵敏度和特异度方面优于八种知名元启发式算法，凸显了其在最优特征选择中的有效性。Ramezani等人（2021）提出了一种增强的MPA变体，集成了反向学习、混沌映射、自适应种群技术和自适应阶段切换机制以改进探索与开发。在CEC-062019测试函数和应用于直流电机的实际控制问题上的仿真表明，该改进算法在准确率和鲁棒性上显著优于原始MPA和其他五种优化算法。Abdel-Basset等人（2021）提出了一种用于优化光伏参数提取的增强MPA，引入种群改进策略：通过自适应变异增强高质量解，低质量解基于最优解和高排名解更新。实验结果表明，该算法提供了更高的准确率，与实测电流-电压数据高度相关，证明了其在参数估计中的有效性。

3.6. 平衡优化器

平衡优化器（EO）受控制系统中动态质量平衡模型启发（Faramarzi等，2020b；Makhadmeh等，2022），其中系统达到平衡状态。EO通过迭代模拟达到平衡的过程，利用浓度更新的控制机制平衡探索与开发。算法利用不同的平衡候选和自适应控制引导搜索过程，维护包含多个平衡候选的平衡池。个体位置向这些候选的更新公式为：

$$X_i(t+1)=X_i(t)+\lambda \cdot \left(X_{\mathrm{eq}}(t)-X_i(t)\right)+F\cdot \left(X_{\mathrm{eq}}(t)-X_{\mathrm{rand}}(t)\right)\text{\hspace{1em}(15)}$$

其中Xeq(t)是迭代t时平衡候选的位置，λ是用于探索的随机控制参数，F是用于开发的控制参数，Xrand(t)是引入多样性的随机解。参数λ和F随时间动态更新以平衡探索与开发：

$$\lambda =1-\frac{t}{T}\text{\hspace{1em}(16)}$$

$$F=\text{rand}(0,1)\text{\hspace{1em}(17)}$$

其中：t为当前迭代次数，T为最大迭代次数。平衡池中的平衡候选更新以反映当前找到的最优解，确保个体被吸引到高质量解同时保持多样性：

$$X_{\mathrm{eq}}(t+1)=X_{\mathrm{best}}(t)+\beta \cdot \left(X_{\mathrm{best}}(t)-X_{\mathrm{mean}}(t)\right)\text{\hspace{1em}(18)}$$

其中：Xbest(t)是迭代t时的最优解，Xmean(t)是种群的平均解，β是控制最优解影响的常数。随着迭代进行，控制参数λ和F通过减少随机波动并鼓励开发，帮助算法向平衡收敛。

Wang等人（2021b）提出了一种利用神经网络丰富光伏电池数据的改进EO，提升优化效率。在三种二极管模型上的测试表明，其优于其他算法，实现了更低的误差率并提高了精度和可靠性，在光伏电池参数估计中高效有效。Abdel-Basset等人（2020）提出了改进的IEO，集成线性递减多样性（LRD）和局部极小消除（MEM）以提升解的准确性和收敛性。LRD通过引导低适应度粒子向最优解移动加速收敛，MEM降低陷入局部极小的风险。在光伏模型上的广泛测试证明了IEO的竞争性能，显示其在太阳能电池应用中的优化优势。Gao等人（2020a）提出了两种用于特征选择的二进制EO（BEO），专为分类任务设计。第一种通过S型和V型传递函数（BEO-S和BEO-V）将连续EO映射为离散形式，第二种（BEO-T）利用当前最优位置。在19个UCI数据集上的测试表明，BEO-V2显著优于其他方法。

3.7. 天鹰优化器

天鹰优化器（AO）受猛禽天鹰的捕猎行为启发（Sasmal等，2023）。AO模拟天鹰强大高效的捕猎策略，结合探索与开发搜索全局最优。算法包含不同的动态运动策略，用于平衡搜索空间的探索和有前景区域的开发（见图6其翱翔与垂直俯冲行为）。

天鹰的初始种群随机生成。AO根据捕猎阶段动态切换不同运动策略：

$$X_i(t+1)=X_{\text{best}}(t)+\alpha \cdot F\left(X_{\text{best}}(t)-X_i(t)\right)\text{\hspace{1em}(19)}$$

在捕猎阶段，计算天鹰与猎物的距离以影响其策略：

$$D=\left|C\cdot X_{\text{best}}(t)-X_i(t)\right|\text{\hspace{1em}(20)}$$

其中D是天鹰i与猎物的距离，C是表示猎物位置影响的系数。在特定情况下，天鹰会更精准地俯冲捕捉猎物，表达式为：

$$X_i(t+1)=X_{\text{best}}(t)+D\cdot e^{b\cdot l}\cdot \sin (2\pi l)\text{\hspace{1em}(21)}$$

其中b控制俯冲宽度，l是控制攻击角度的随机变量，e是自然对数底，指示俯冲的锐利度。AO使用自适应参数动态调整搜索，例如α随时间变化以平衡探索与开发：

$$\alpha =2\cdot \left(1-\frac{t}{T}\right)\cdot \text{rand}(0,1)\text{\hspace{1em}(22)}$$

其中T是总迭代次数，t是当前迭代次数。

Al-qaness等人（2022）通过改进AO和反向学习（OBL）优化自适应神经模糊推理系统（ANFIS）的参数，解决了其在石油产量估计中的不足。该模型在真实数据集和均方根误差（RMSE）、平均绝对误差（MAE）等性能指标上优于多种改进ANFIS模型和时间序列预测方法。Mahajan等人（2022）提出了结合AO和算术优化算法（AOA）的混合优化方法以提升收敛性和解质量。该AO-AOA方法在图像处理和工程设计等多种问题上进行了评估，在高维和低维问题中表现一致，基于种群的方法在高维优化中有效。Bas（2023）提出了用于解决二进制优化问题的二进制AO（BAO），对基于连续的AO进行更新。BAO使用传递函数将连续搜索空间转换为二进制空间，包含两种变体：BAO-T和BAO-CM（集成交叉和变异步骤）。在63个背包问题数据集上的测试表明，BAO-CM优于BAO-T和其他最新启发式算法，展示了其在二进制优化任务中的有效性。

3.8. 海鸥优化算法

Dhiman和Kumar（2019）提出了海鸥优化算法（Seagull Optimization Algorithm，SOA），这是一种基于海鸥迁徙和攻击行为的生物启发式方法，旨在增强搜索空间内的探索与开发能力。SOA的性能通过44个测试函数与9种流行元启发式算法进行了基准对比，并评估了其计算复杂度和收敛行为。此外，SOA被应用于7个受约束的实际工业问题，展示了其在解决大规模复杂优化挑战中的有效性。实验结果表明，SOA具有高度竞争力，非常适合解决受约束的高计算成本问题。

海鸥的行为可描述如下：（i）迁徙期间，海鸥以群体形式飞行，从不同位置出发以避免相互碰撞；（ii）在群体内，海鸥会向适应度最高的个体（即与其他海鸥相比适应度值最低的个体）调整移动方向；（iii）以适应度最高的海鸥位置为参考，其他海鸥可调整其初始位置。海鸥在从一个地点迁移到另一个地点时，常对海上迁徙的鸟类发起攻击，攻击过程中采用自然螺旋运动。这些行为可针对目标函数进行公式化建模以实现优化目标。

在迁徙阶段，算法模拟海鸥群体从一个位置移动到另一个位置的行为。在此阶段，海鸥需满足三个条件：（i）碰撞避免：为防止与邻近海鸥碰撞，在计算搜索代理新位置时引入额外变量A：

$${\vec{C}}_s=Ax{\vec{P}}_s(x)\text{\hspace{1em}(23)}$$

其中，${\vec{C}}_s$表示不与其他搜索代理发生碰撞的搜索代理位置，${\vec{P}}_s$表示搜索代理的当前位置，x指当前迭代次数，A表示搜索代理在指定搜索空间内的移动行为。（ii）向最优邻居方向移动：在避免与邻居碰撞后，搜索代理向最优邻居代理方向移动：

$${\vec{M}}_s=Bx\left(\overrightarrow{P_{bs}}(x)-\overrightarrow{P_s}(x)\right)\text{\hspace{1em}(24)}$$

其中，${\vec{M}}_s$表示搜索代理${\vec{P}}_s$相对于最优搜索代理$\overrightarrow{P_{bs}}$（适应度最高的海鸥）的位置。B的行为是随机的，有助于维持探索与开发之间的适当平衡。（iii）保持靠近最优搜索代理：最后，搜索代理可相对于最优搜索代理调整其位置：

$$\overrightarrow{D_s}=\left|{\vec{C}}_s+{\vec{M}}_s\right|\text{\hspace{1em}(25)}$$

其中，$\overrightarrow{D_s}$表示搜索代理与最优搜索代理（即适应度值最低的最优海鸥）之间的距离。

开发阶段旨在利用搜索过程中积累的历史经验。海鸥在迁徙时能够持续调整攻击角度和速度，通过翅膀和体重调节高度。追击猎物时，它们在空中呈现螺旋运动模式。这种在x、y和z平面上的行为描述如下：

$$x^{\prime }=rx\cos (k)$$

$$y^{\prime }=rx\sin (k)$$

(26)

$$z^{\prime }=r\times k$$

$$r=ux{e}^{kv}$$

其中，r表示螺旋每圈的半径，k是[0≤k≤2π]范围内的随机数，u和v是决定螺旋形状的常数，e为自然对数的底。搜索代理的更新位置通过公式27计算：

$${\vec{P}}_s(x)=\left({\vec{D}}_{s}x{x}^{\prime }x{y}^{\prime }x{z}^{\prime }\right)+\overrightarrow{P_{bs}}(x)\text{\hspace{1em}(27)}$$

其中，${\vec{P}}_s(x)$存储最优解并更新其他搜索代理的位置。

Panagant等（2020）提出了一种用于形状优化的替代模型辅助元启发式方法，将SOA应用于车辆支架结构形状优化。目标是在满足应力约束的同时最小化结构质量。有限元分析（FEA）用于函数评估，并辅以克里金模型进行估计。结果表明，SOA表现出与鲸鱼优化算法和樽海鞘群优化算法相当的竞争力，显示出在工业部件设计中的强大潜力。Jia等（2019）提出了三种将SOA与热交换优化（TEO）结合的混合算法用于特征选择。第一种算法采用轮盘赌策略在SOA和TEO之间交替进行位置更新；第二种方法在SOA迭代后应用TEO；第三种方法将TEO的热交换公式集成到SOA的攻击模式中以增强开发能力。这些混合算法在分类准确率和特征选择效率上均有提升，与现有混合优化方法相比，在减少CPU时间的同时取得了竞争性结果。Dhiman等（2021）提出了多目标SOA（MOSOA），通过动态存档存储非支配帕累托最优解，并采用轮盘赌选择方法有效选择存档解，模拟海鸥的迁徙和攻击行为。MOSOA在24个基准函数上进行了测试，并与现有元启发式算法对比。此外，其被应用于6个受约束的工程设计问题，展示了帕累托最优解的优越性能和高收敛性，非常适合复杂的实际应用。

3.9. 蝠鲼觅食优化算法

蝠鲼觅食优化（Manta Ray Foraging Optimization，MRFO）算法受蝠鲼觅食行为启发，通过特定运动策略兼顾探索与开发（Zhao等，2020b）。二维空间中三只蝠鲼的空翻觅食行为如图7所示。

在探索阶段，蝠鲼通过螺旋运动搜索猎物，其更新方程建模如下：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^t+A\cdot \left(\cos (\theta )\cdot \left({\mathbf{X}}_i^t-{\mathbf{X}}_{\text{best}}^t\right)+\sin (\theta )\cdot \left({\mathbf{X}}_i^t-{\mathbf{X}}_{\text{mean}}^t\right)\right)$$

其中，A为缩放因子，θ为[0,2π]范围内的随机角度，${\mathbf{X}}_{\text{best}}^t$为当前找到的最优解位置，${\mathbf{X}}_{\text{mean}}^t$为种群平均位置。在开发阶段，蝠鲼通过调整位置向最优解移动，更新方程如下：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_{\text{best}}^t+B\cdot \left({\mathbf{X}}_i^t-{\mathbf{X}}_{\text{best}}^t\right)$$

其中，B为影响向最优解移动的随机因子。

此外，蝠鲼可能对最优解进行局部搜索：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^t+F\cdot \left({\mathbf{X}}_{\text{best}}^t-{\mathbf{X}}_i^t\right)$$

其中，F为控制搜索强度的随机因子。

蝠鲼通过调整向猎物位置的移动来搜索猎物，这一行为表示为：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^t+C\cdot \left({\mathbf{X}}_{\text{prey}}^t-{\mathbf{X}}_i^t\right)$$

其中，C为缩放因子，${\mathbf{X}}_{\text{prey}}^t$为猎物位置。

为避免陷入局部最优，算法采用多样化机制，使每个解探索搜索空间的新区域：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^t+D\cdot \left({\mathbf{X}}_{\text{worst}}^t-{\mathbf{X}}_i^t\right)$$

其中，D为缩放因子，${\mathbf{X}}_{\text{worst}}^t$为最差解位置。

MRFO算法通过迭代探索与开发阶段，直至满足终止条件（如最大迭代次数或收敛阈值）。

Tang等（2021）提出了改进的MRFO（m-MRFO），通过精英搜索池、自适应控制参数和分布估计策略提升性能。在23个测试函数和CEC2017上的验证表明，m-MRFO显著改进了性能，并适用于实际工程设计问题。Houssein等（2021）提出了MRFO-OBL算法，这是MRFO的增强版本，结合了反向学习（OBL）以提高种群多样性并避免局部最优。MRFO-OBL通过多级阈值处理解决COVID-19 CT图像分割问题，并与包括原始MRFO在内的6种元启发式算法对比。结果表明，MRFO-OBL在峰值信噪比和结构相似性指数等指标上表现出更优的分割质量、一致性和鲁棒性，优于所有对比算法。Hassan等（2021）提出了一种将MRFO与基于梯度的优化器（GBO）结合的创新方法，用于解决经济排放调度（EED）问题。这种集成旨在提升求解速度并降低原始MRFO陷入局部最优的概率。MRFO-GBO同时处理单目标和多目标EED挑战，并采用模糊集理论识别多目标场景下的最优解。该算法通过CEC’17测试函数验证，并应用于三种不同发电机配置的电力系统EED场景。结果表明，MRFO-GBO优于原始MRFO和GBO，在解决EED问题时展现出更优的精度、鲁棒性和收敛特性。

3.10. 黑猩猩优化算法

黑猩猩优化算法（Chimp Optimization Algorithm，ChOA）受黑猩猩的智能捕猎和社会合作行为启发（Khishe和Mosavi，2020）。该算法通过模拟黑猩猩的捕猎策略，在优化过程中平衡探索与开发。ChOA在黑猩猩群体中纳入四种主要角色：攻击者、驱赶者、阻挡者和追逐者，每种角色对应不同的搜索行为。

黑猩猩初始种群随机生成。通过四种群体（攻击者、驱赶者、阻挡者和追逐者）的共同作用模拟黑猩猩捕猎行为，每种群体在接近猎物（解）时扮演不同角色。位置更新规则受最优黑猩猩位置影响：

$$X_i(t+1)=X_{\text{best}}(t)-A\cdot D\text{\hspace{1em}(28)}$$

其中，$X_{\text{best}}(t)$为第t次迭代时最优黑猩猩的位置，A为控制方向和步长的系数，D表示黑猩猩i与猎物（最优解）之间的距离。系数A计算如下：

$$A=2\cdot a\cdot r-a\text{\hspace{1em}(29)}$$

其中，a在迭代过程中从2线性递减至0，平衡探索与开发；r为0到1之间的随机数。黑猩猩与猎物之间的距离计算为：

$$D=\left|C\cdot X_{\text{best}}(t)-X_i(t)\right|\text{\hspace{1em}(30)}$$

其中，C为另一个控制探索阶段的系数，计算为：

$$C=2\cdot r\text{\hspace{1em}(31)}$$

黑猩猩根据计算的系数及其在群体中的角色在探索与开发之间切换。不同角色（攻击者、驱赶者、阻挡者和追逐者）通过数学建模确保搜索机制的平衡。参数a随时间递减，使算法从探索过渡到开发，随着迭代推进引导黑猩猩趋向更优解。

$$a(t)=2-\frac{t}{T}\text{\hspace{1em}(32)}$$

其中：t为当前迭代次数，T为最大迭代次数。

Khishe等（2021）提出了加权ChOA以解决大规模数值优化中收敛速度慢和局部最优问题。位置加权方程增强了收敛性并避免局部最优，改进了探索与开发的平衡。在30个基准函数、IEEE竞赛基准和高维实际问题上的测试表明，该算法在速度和优化精度上表现更优。Jia等（2021b）提出了增强型ChOA（EChOA）以提高求解精度。EChOA采用多项式变异优化种群初始化，利用斯皮尔曼等级相关比较黑猩猩的社会地位，并通过甲虫触角算子改进探索和避免局部最优。在12个经典基准、15个CEC2017函数和实际工程问题上的测试表明，EChOA优于ChOA和其他5种算法，展示了强大的优化能力和实际应用潜力。Du等（2022）提出了改进型ChOA（IChOA），结合空翻觅食策略与自适应权重解决3D路径规划挑战。通过原始ChOA导出的权重因子动态调整位置向量更新方程，空翻策略有助于避免局部最优并增强早期种群多样性。在CEC2019函数和3D路径规划场景中的测试表明，IChOA与其他方法相比具有竞争力。

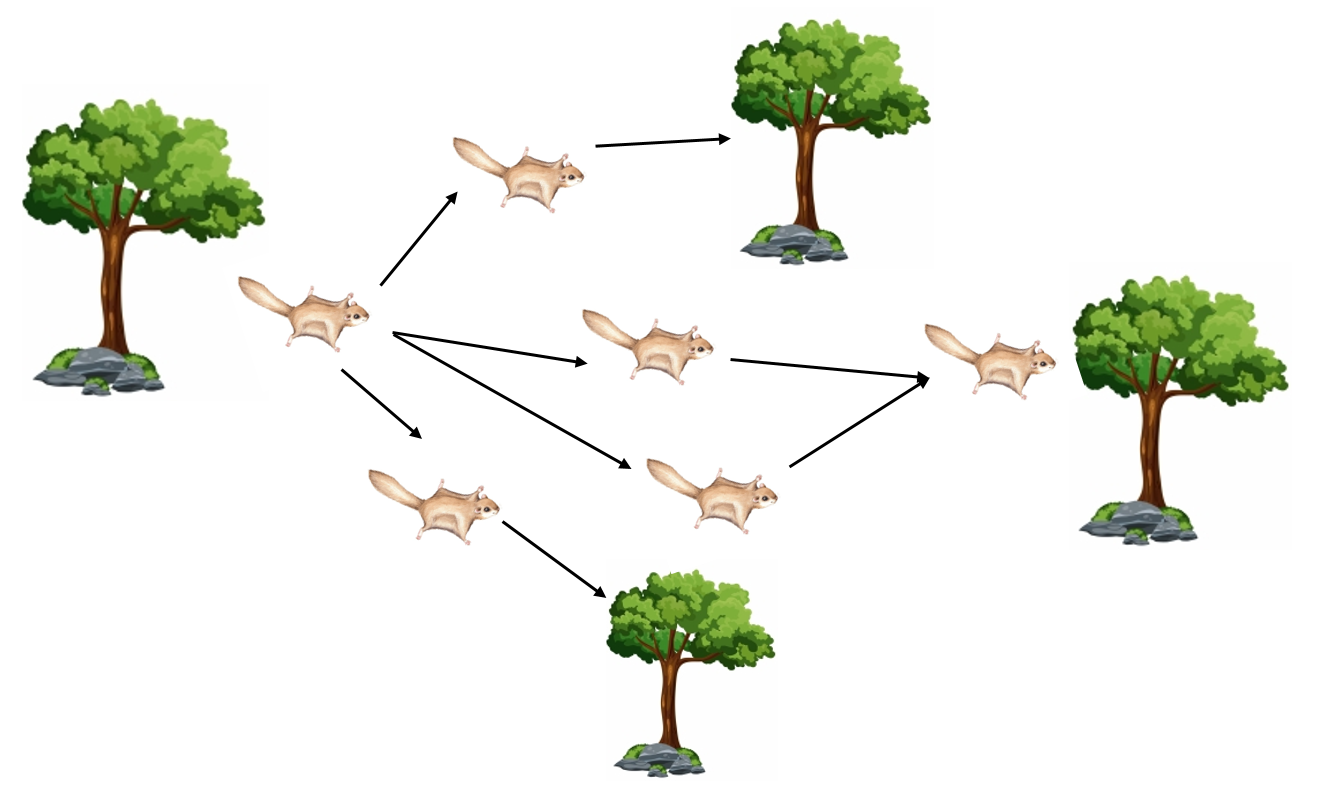
3.11. 松鼠搜索算法

松鼠搜索算法（Squirrel Search Algorithm，SSA）模拟飞鼠的觅食行为，涉及探索与开发（Jain等，2019）。该算法以随机搜索移动和围绕发现食物源的局部搜索为特征。松鼠在树间飞行的行为如图8所示。

在探索阶段，松鼠通过在空间中随机移动搜索食物源，建模为：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^t+\alpha \cdot \text{rand}\cdot \left({\mathbf{X}}_i^t-{\mathbf{X}}_{\text{best}}^t\right),$$

其中，α为缩放因子，rand为[0,1]之间的随机数，${\mathbf{X}}_{\text{best}}^t$为当前找到的最优松鼠位置。

在开发阶段，松鼠通过围绕当前找到的最优食物源进行局部搜索来利用已发现的食物源，开发移动方程为：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_{\text{best}}^t+\beta \cdot \left({\mathbf{X}}_i^t-{\mathbf{X}}_{\text{best}}^t\right),$$

其中，β为决定围绕最优解搜索强度的随机因子。

此外，松鼠可能围绕当前解进行随机游走：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^t+\gamma \cdot \text{rand}\cdot \left({\mathbf{X}}_i^t-{\mathbf{X}}_{\text{mean}}^t\right),$$

其中，γ为缩放因子，${\mathbf{X}}_{\text{mean}}^t$为种群平均位置。

松鼠通过适应度评估食物源，位置更新受最优食物源适应度影响：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^t+\delta \cdot \left({\mathbf{X}}_i^t-{\mathbf{X}}_{\text{food}}^t\right)$$

其中，δ为随机缩放因子，${\mathbf{X}}_{\text{food}}^t$为适应度最优的食物源位置。

为防止过早收敛，松鼠采用多样化机制探索搜索空间的其他区域，该阶段建模为：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^t+\epsilon \cdot \left({\mathbf{X}}_{\text{worst}}^t-{\mathbf{X}}_i^t\right)$$

其中，ε为多样化因子，${\mathbf{X}}_{\text{worst}}^t$为最差解位置。

Zheng和Luo（2019）提出了改进的SSA（ISSA）以增强全局收敛性。ISSA包含以下改进：自适应捕食者存在概率以平衡探索与开发、正态云模型捕捉觅食随机性、连续位置选择策略保留最优位置、维度搜索增强改进局部搜索。在32个基准函数（包括单峰、多峰和CEC 2014函数）上的测试表明，ISSA表现出竞争力，优于基础SSA和其他4种先进算法。Dhaini和Mansour（2021）将SSA应用于解决无约束和受约束的投资组合优化问题。投资组合优化旨在寻求最优资产配置，传统上通过均值-方差模型（Markowitz）及其扩展（包括夏普模型）解决。利用自然启发算法的成功，该研究将SSA适配于两类问题，并与多种经典、混合和多目标方法对比。结果表明，SSA在无约束优化中表现卓越，在受约束场景中具有竞争力，在不同模型和评估指标上均取得更优性能。Sakthivel等（2021）提出了多目标SSA以解决综合经济与环境电力调度问题（因环境问题日益受到关注）。该SSA集成帕累托支配生成非支配解，采用带拥挤距离排序的外部精英库确保帕累托最优解的多样性。在三个复杂系统上的测试表明，与其他先进启发式方法相比，该算法在成本与排放的权衡中表现更优。

3.12. 亨利气体溶解度优化算法

亨利气体溶解度优化算法（Henry Gas Solubility Optimization, HGSO）是一种受液体溶液中气体分子行为启发的元启发式算法，其基础是亨利定律（Hashim等，2019）。该算法模拟了气体粒子在解空间中如何相互作用并向最优解收敛的过程。在HGSO中，每个分子根据其浓度和溶解度系数kₕ（亨利常数）调整位置，这两个因素会影响每个分子的移动强度。

每个分子的浓度Cᵢ会被更新以反映其解的质量：

$$C_i^{(t+1)}=C_i^{(t)}+\alpha \left(C_{\mathrm{best}}-C_i^{(t)}\right)$$

其中C_best为当前找到的最优解的浓度，α为学习因子，控制C_best对Cᵢ的影响程度。

每个分子的溶解度受亨利系数影响，该系数通过蒸发函数更新：

$$k_H^{(t+1)}=k_H^{(t)}\cdot e^{-\beta \cdot t}$$

其中β为衰减参数，t为当前迭代次数。该系数调节搜索强度，随迭代进行逐渐减小以促进收敛。

每个分子的新位置由浓度和溶解度效应共同决定：

$${\mathbf{x}}_i^{(t+1)}={\mathbf{x}}_i^{(t)}+k_H^{(t)}\left(C_{\text{best}}-C_i^{(t)}\right)\cdot \text{randn}\left({\mathbf{x}}_i\right)$$

其中randn(xᵢ)为高斯分布随机数，用于引入可控的随机行为。

算法在达到最大迭代次数T或最优解变化小于阈值ε时停止：

$$\Vert {\mathbf{x}}_{\text{best}}^{(t+1)}-{\mathbf{x}}_{\text{best}}^{(t)}\Vert <ϵ$$

HGSO算法采用了受液体中气体溶解度启发的机制，通过浓度和溶解度系数引导搜索过程。通过逐步降低探索强度，HGSO确保了向最优解的有效收敛。

Neggaz等人（2020）提出了一种使用HGSO算法进行特征选择（FS）的新方法，解决了大型数据集易陷入局部最优的问题。在KNN和SVM分类器上的多种数据集测试表明，HGSO性能优于GOA和WOA等其他元启发式算法。统计测试证实了其有效性，在超过11,000个特征的数据集上实现了高达100%的准确率。Yildiz等人（2021b）提出了混沌HGSO（CHGSO）算法，该元启发式算法将混沌映射集成到原始HGSO中，以增强复杂工程优化问题的收敛性。作为与问题无关的算法，CHGSO在焊接梁设计、悬臂梁设计、汽车制造和膜片弹簧设计等多种约束优化任务中进行了测试。与现有算法的对比结果表明，当结合合适的混沌映射时，CHGSO在机械设计和制造挑战中表现出鲁棒性和求解最优解的有效性。Abd Elaziz和Attiya（2021）提出了一种改进的HGSO算法，用于云计算中的最优任务调度。通过集成用于局部搜索的鲸鱼优化算法（WOA）和用于解改进的综合反向学习（COBL），HGSWC旨在提高任务到资源的映射效率。在36个基准函数上的验证以及合成和真实调度任务的测试表明，HGSWC性能优于传统HGSO、WOA和其他六种元启发式算法，以最小的计算开销实现了接近最优的解。

3.13. 阿基米德优化算法

阿基米德优化算法（Archimedes Optimization Algorithm, AOA）是一种受阿基米德原理（特别是浮力和密度原理）启发的元启发式优化算法（Hashim等，2021）。该算法模拟了浸没在流体中的物体所受的浮力，通过随时间调整解的密度和体积来平衡探索（搜索新解）和利用（优化现有解）。AOA算法随机生成初始候选解。其核心是浮力计算，基于阿基米德原理：

$$F_b=\rho \cdot V\cdot g\text{\hspace{1em}(33)}$$

其中F_b为浮力，ρ为流体密度（与解的质量相关），V为物体体积（候选解），g为重力加速度常数。候选解的位置根据计算的浮力和密度更新：

$$X_i(t+1)=X_i(t)+F_b\cdot \left(1-\frac{\rho }{{\rho }_{\max }}\right)\text{\hspace{1em}(34)}$$

其中Xᵢ(t+1)为解i在t+1时刻的新位置，F_b为作用于该解的浮力，ρ_max为最大允许密度，用于控制搜索的探索-利用平衡。算法动态调整解的密度和体积以平衡探索与利用。随着算法推进，密度增加以聚焦利用：

$$\rho ={\rho }_{\min }+\left({\rho }_{\max }-{\rho }_{\min }\right)x\left(\frac{t}{T}\right)\text{\hspace{1em}(35)}$$

其中ρ_min和ρ_max定义密度范围，t为当前迭代次数，T为总迭代次数。AOA包含自适应机制，随时间调整探索与利用的平衡。以下方程展示了体积随算法收敛而减小的过程：

$$V=V_{\max }x\left(1-\frac{t}{T}\right)\text{\hspace{1em}(36)}$$

其中V_max为最大体积，体积V随t增加而减小，促进算法后期的利用阶段。

Yildiz等人（2021a）研究了AOA在最小化产品开发成本中的应用。该研究通过尺寸、形状和拓扑优化聚焦于车辆结构优化，展示了POA优越的搜索能力和计算效率。Akdag（2022）提出了改进AOA（IAOA）以解决最优潮流（OPF）问题。IAOA增强了种群多样性并平衡了利用与探索以防止早熟收敛。在IEEE和南马尔马拉系统上的测试表明，与不同技术的对比仿真结果显示IAOA在最小化燃料排放方面具有鲁棒性。Desuky等人（2021）提出了增强AOA（EAOA）用于特征选择，通过添加步长参数改进了原始AOA的探索-利用平衡。在23个基准函数和16个真实数据集上的测试表明，EAOA在分类性能和优化结果上优于AOA和其他知名算法。16个真实数据集的结果证实，EAOA选择的约简特征子集显著提升了分类性能。

3.14. 被囊动物群算法

被囊动物群算法（Tunicate Swarm Algorithm, TSA）受被囊动物（又称海鞘）的群体行为启发，特别是其社交互动和觅食策略（Kaur等，2020）。被囊动物表现出独特的行为，使其能有效寻找食物并适应环境。TSA捕捉这些行为以构建解决复杂优化问题的高效搜索机制。被囊动物具备在海洋中定位食物源的能力，但在指定搜索区域内缺乏食物源的先验信息。本文利用观察到的被囊动物两种行为定位最优食物源：喷射推进和群体智能。

为建立喷射推进行为的数学模型，被囊动物需满足三个条件：避免搜索代理间的冲突、向最有效搜索代理的位置移动、保持与最优搜索代理的接近。相比之下，群体行为促进其他搜索代理位置相对于最优解的更新。为避免群体中其他被囊动物（搜索代理）间的冲突，利用向量$\vec{A}$计算搜索代理新位置（公式37）：

$$\vec{A}=\vec{G}+\vec{M}\text{\hspace{1em}(37)}$$

$\vec{G}$表示重力，$\vec{M}$表示搜索代理间的社会力。向量$\vec{M}$的计算为：

$$\vec{M}=\lfloor P_{\min }+c_1\cdot \left(P_{\max }-P_{\min }\right)\rfloor \text{\hspace{1em}(38)}$$

P_min和P_max表示促进社会互动的初始和次级速度。在Kaur等（2020）中，P_min和P_max分别设为1和4。冲突解决后，搜索代理向最优邻居方向移动，计算式为：

$$\overrightarrow{PD}=\left|\overrightarrow{FS}-r_{\text{and}}\cdot {\vec{P}}_p(x)\right|\text{\hspace{1em}(39)}$$

其中$\overrightarrow{PD}$为食物源与搜索代理（被囊动物）间的距离，x为当前迭代，$\overrightarrow{FS}$为食物源位置（最优解），${\vec{P}}_p(x)$为被囊动物位置，r_rand为指定范围内的随机数。随后，搜索代理相对于最优搜索代理（食物源）定位，公式为：

$${\vec{P}}_p\left(x^{\prime }\right)=\{\begin{array}{ll}\vec{F}S+\vec{A}\cdot {\vec{P}}_D,& \text{ifrand}\ge 0.5\\ \vec{F}S-\vec{A}\cdot {\vec{P}}_D,& \text{ifrand}<0.5\end{array}\text{\hspace{1em}(40)}$$

其中${\vec{P}}_p\left(x^{\prime }\right)$为食物源$\overrightarrow{FS}$位置下被囊动物的更新位置。为数学模拟被囊动物的群体行为，记录前两个最优解，使其他搜索代理能基于最优代理位置更新。以下公式描述该群体行为：

$${\vec{P}}_p(x+1)=\frac{{\vec{P}}_p(x)+{\vec{P}}_p(x+1)}{2+c_1}\text{\hspace{1em}(41)}$$

搜索代理根据最优代理更新位置为${\vec{P}}_p\left(x^{\prime }\right)$，最终位置随机位于由被囊动物位置定义的圆柱或锥形区域内。

Houssein等（2021）提出了结合局部逃逸算子（LEO）的增强TSA，以解决原始TSA的局限性。LEO策略防止搜索停滞并提升群体代理的收敛速度和局部搜索效率。TSA-LEO的有效性在CEC’2017测试集上验证，并与其他七种元启发式算法对比。结果表明LEO显著提升了TSA的解质量和收敛速度。Rizk-Allah等（2021）提出增强TSA（ETSA），改进了探索与利用能力。ETSA在20个基准函数（包括单峰和多峰测试）上评估并与其他算法对比。统计分析证实其鲁棒性和有效性，ETSA在高维场景中表现出恢复力且通常比竞争方法需要更少CPU时间。最终，ETSA在经济调度问题中的应用展示了其在实际优化任务中的有效性。Gharehchopogh（2022）通过引入变异算子（Lévy、柯西和高斯变异算子）提升TSA性能，以解决全局优化问题。作者提出的新算法利用这些算子在不同阶段对优化过程产生不同贡献。该算法在单峰、多峰基准函数及六个大规模工程问题上测试，实验结果表明QLGCTSA算法优于竞争优化算法，展示了其解决复杂优化任务的有效性。

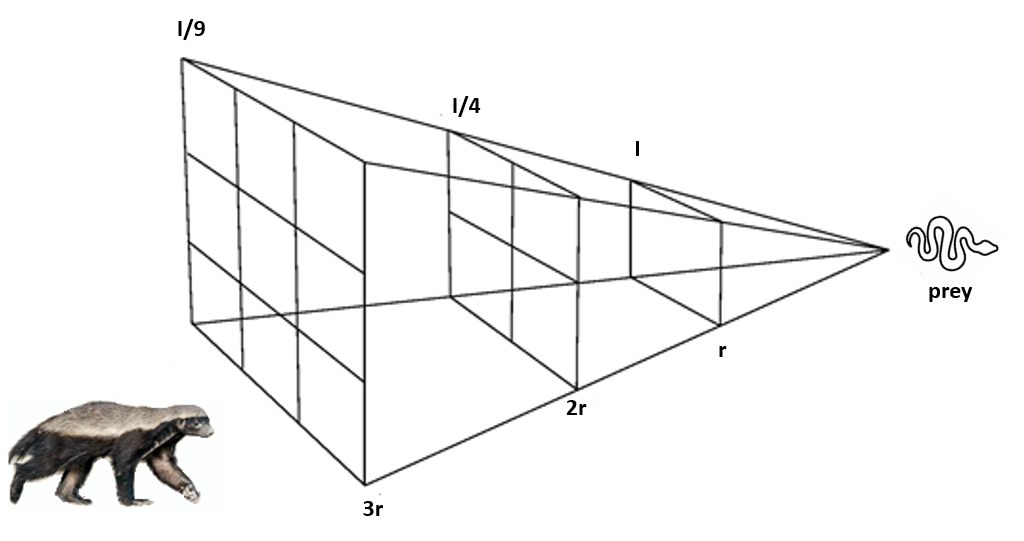
3.15. 蜜獾算法

蜜獾算法（Honey Badger Algorithm, HBA）受蜜獾的觅食行为和无畏特性启发（Hashim等，2022）。该算法通过群体代理探索搜索空间，平衡探索与利用，旨在解决复杂优化问题。算法整合了局部搜索、随机移动和层级结构等策略，使其能逃离局部最优并高效收敛至全局解。HBA已应用于工程、金融和机器学习等领域，表现出优于其他优化算法的性能。图9展示了蜜獾使用的平方反比定律技术。

在探索阶段，蜜獾通过随机搜索移动探索搜索空间，位置更新方程为：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^t+\alpha \cdot \text{rand}\cdot \left({\mathbf{X}}_i^t-{\mathbf{X}}_{\text{best}}^t\right)$$

其中α为缩放因子，rand为[0,1]间随机数，X_best^t为当前最优解。

在利用阶段，蜜獾通过局部搜索机制利用最优解更新位置：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_{\text{best}}^t+\beta \cdot \left({\mathbf{X}}_i^t-{\mathbf{X}}_{\text{best}}^t\right)$$

其中β为决定向最优解移动的随机因子。

若蜜獾接近食物源，则进行更激进的搜索：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^t+\gamma \cdot \left({\mathbf{X}}_{\text{best}}^t-{\mathbf{X}}_i^t\right)$$

其中γ为控制激进搜索强度的因子。

为模拟避敌行为，蜜獾应用多样化机制避免局部最优并探索搜索空间其他区域，该阶段模型为：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^t+\delta \cdot \left({\mathbf{X}}_{\text{worst}}^t-{\mathbf{X}}_i^t\right)$$

其中δ为缩放因子，X_worst^t为当前最差解位置。

蜜獾通过向食物源移动觅食，食物源吸引力更新为：

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^t+\epsilon \cdot \left({\mathbf{X}}_{\text{food}}^t-{\mathbf{X}}_i^t\right)$$

其中ε为缩放因子，X_food^t为食物源位置。

Duzenli等（2022）聚焦于通过两种改进HBA增强光伏参数估计的收敛性。第一种变体结合高斯/鼠映射混沌方法优化探索与利用，第二种混合反向学习以高效扫描搜索空间。在CEC2017和CEC2019数据集上的评估表明，这些算法在优化单二极管、双二极管及多晶、单晶等光伏模型参数中表现出色。Fathy等（2023）提出了一种微电网（MG）能源管理方案，利用HBA优化光伏（PV）、风力发电机（WT）、微型涡轮机（MT）、燃料电池（FC）和电池存储等发电单元的调度。HBA有效平衡探索与利用，避免复杂优化问题中的局部最优。研究分析了三种运行场景：正常PV和WT发电、WT额定功率、两者最大限制。该研究聚焦两个目标：降低运行成本和最小化污染物排放，同时对比HBA与其他优化算法的性能。结果表明HBA在所有测试条件下表现出优越的鲁棒性和有效性，是提升微电网运行的有力候选。

3.16. 蜉蝣优化算法

蜉蝣优化算法（Mayfly Optimization Algorithm, MOA）受蜉蝣群集和交配行为启发（Zervoudakis & Tsafarakis，2020b）。MOA模拟雌雄蜉蝣间的动态以有效探索解空间。种群由雌雄蜉蝣组成，其位置表示可能的解，通过吸引、交配和移动规则随时间进化。算法迭代直至收敛到最优解或达到最大迭代次数。

雄蜉蝣基于对其他雄蜉蝣的吸引和向种群中最优蜉蝣的引力更新速度。雄蜉蝣Mⁱ的速度更新为：

$${\mathbf{V}}_M^i(t+1)=w\cdot {\mathbf{V}}_M^i(t)+r_1\cdot \alpha \cdot \left({\mathbf{M}}^{\text{best}}-{\mathbf{M}}^i(t)\right)+r_2\cdot \beta \cdot \left({\mathbf{M}}^j-{\mathbf{M}}^i(t)\right)$$

其中：- w为惯性权重；- r₁和r₂为[0,1]均匀分布随机数；- α和β为吸引系数；- M_best为最优雄蜉蝣位置；- Mʲ为邻近雄蜉蝣位置。

雄蜉蝣新位置计算为：

$${\mathbf{M}}^i(t+1)={\mathbf{M}}^i(t)+{\mathbf{V}}_M^i(t+1)$$

雌蜉蝣被对应的雄配偶吸引，雌蜉蝣Fⁱ的速度更新为：

$${\mathbf{V}}_F^i(t+1)=w\cdot {\mathbf{V}}_F^i(t)+r_3\cdot \gamma \cdot \left({\mathbf{M}}^i-{\mathbf{F}}^i(t)\right)$$

其中：- w为惯性权重；- r₃为[0,1]均匀分布随机数；- γ为雌向雄的吸引系数；- Mⁱ为对应雄蜉蝣位置。

雌蜉蝣新位置计算为：

$${\mathbf{F}}^i(t+1)={\mathbf{F}}^i(t)+{\mathbf{V}}_F^i(t+1)$$

当雌雄蜉蝣距离变近（即搜索空间中接近时），发生交配并产生后代。后代继承双亲特征，初始位置为：

$${\mathbf{O}}^i=\delta \cdot {\mathbf{M}}^i+(1-\delta )\cdot {\mathbf{F}}^i$$

其中δ∈[0,1]为控制双亲对后代位置贡献的权重因子。

算法在满足终止条件（如最大迭代次数或解的满意适应度）时停止。

Gao等（2020b）将MOA与PSO和差分进化（DE）结合，基于笛卡尔距离改进速度更新，增强个体间移动。仿真表明该改进MO版本优于原始算法，提供更好的优化和收敛。Shaheen等（2021）提出混沌MOA（CMOA）以精确建模质子交换膜燃料电池（PEMFC）。通过优化制造商数据中缺失的七个设计变量，CMOA最小化实验室测量电压与仿真电压的总平方误差，解决PEMFC的非线性I-V特性。混沌映射与MOA的集成提升了解质量。该模型在不同PEMFC类型和条件（温度、压力）下测试，结果表明CMOA实现了精确仿真，经其他优化方法验证，为PEMFC建模提供了鲁棒可靠的方案。Nagarajan等（2022）提出改进MOA（IMA）结合Lévy飞行解决微电网联合经济排放调度（CEED）问题，旨在优化发电成本和最小化排放。研究聚焦包含火电、太阳能和风电的离网微电网，在24小时变需求场景下测试。IMA在四种场景中显著降低成本和排放，优于原始蜉蝣算法及其他方法，凸显其在并网微电网CEED优化中的有效性。

3.17. 非洲秃鹫优化算法

非洲秃鹫优化算法（African Vulture Optimization Algorithm, AVOA）受秃鹫食腐行为启发（Abdollahzadeh等，2021a）。算法模拟非洲秃鹫通过大范围探索和发现食物源时的聚集行为。在AVOA中，秃鹫表示在问题空间中搜索最优解的代理，每个代理基于探索（搜索新区域）和利用（聚焦已知有前景区域）调整位置。AVOA的探索-利用平衡使其适用于工程设计、机器学习和调度等领域的高效优化（见图10非洲秃鹫争食时的整体向量）。

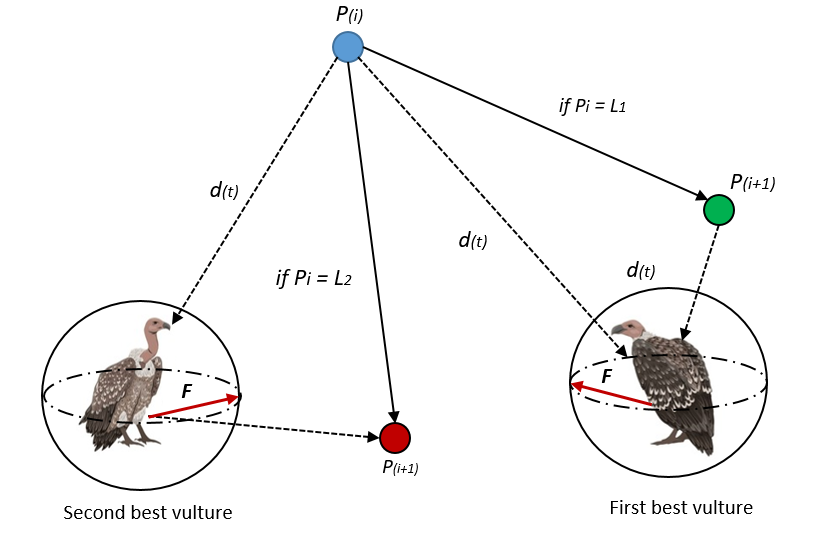
每只秃鹫的位置在每次迭代中基于当前猎物（最优解）位置更新，位置更新方程为：

$$X_i(t+1)=X_{\text{prey}}(t)+A\cdot D\text{\hspace{1em}(42)}$$

其中Xᵢ(t+1)为秃鹫i在t+1时刻的更新位置，X_prey(t)为当前猎物位置，A和D为控制猎物位置影响的自适应参数。秃鹫与猎物间的距离用于引导移动，计算为：

$$D=\left|C\cdot X_{\text{prey}}(t)-X_i(t)\right|\text{\hspace{1em}(43)}$$

D表示秃鹫i与猎物的距离，C为基于环境因素缩放距离的系数。

在部分算法变体中，秃鹫可绕猎物螺旋移动以模拟更复杂的搜索，螺旋运动描述为：

$$X_i(t+1)=D\cdot e^{b\cdot l}\cdot \cos (2\pi l)+X_{\text{prey}}(t)\text{\hspace{1em}(44)}$$

b控制螺旋宽度，l为控制螺旋角度的随机变量，e为自然对数底，表示螺旋的指数特性。为平衡探索与利用，算法采用随时间变化的两个自适应系数A和C，定义为：

$$A=2\cdot a\cdot \text{rand}(0,1)-a\text{\hspace{1em}(45)}$$

$$C=2\cdot rand(0,1)\text{\hspace{1em}(46)}$$

其中a为随时间递减的变量，促进算法收敛时的利用。

Askr等（2023）提出了多目标AVOA（MaAVOA），在选择过程中引入新的社会领导秃鹫和基于池的环境选择机制。通过DTLZ函数（Tanabe & Oyama，2017）和实际问题实验，MaAVOA在收敛性、多样性和统计相关性上优于现有算法，成为复杂工程问题的有前景解决方案。Alanazi等（2022）研究了受辐照和温度等天气条件显著影响的光伏（PV）系统，局部阴影条件（PSC）会导致热点和功率损失。他们引入AVOA优化PSC下的PPV阵列重构以最大化发电。五种阴影模式的对比研究表明，AVOA在功率提升和性能比上优于其他方法。建议使用混沌映射微调AVOA参数以提升结果。Fan等（2021）开发了新元启发式算法（TAVOA），通过帐篷混沌映射初始化种群和时变机制平衡探索与利用改进AVOA。在基准函数和实际工程问题上的测试表明，TAVOA在多案例中显著优于AVOA和其他先进算法，展示了改进的优化能力。

3.18. 金豺优化算法

金豺优化算法（Golden Jackal Optimization, GJO）是一种受金豺捕猎行为和社会等级启发的新型群体元启发式算法（Chopra & Ansari，2022）。与其他自然启发算法类似，GJO在搜索过程中模拟金豺协作捕猎和资源共享的方式，平衡探索与利用。见图11金豺的搜索与攻击阶段。

GJO利用多种关键机制优化复杂问题。在探索阶段，金豺通过模拟随机和集体移动模式搜索解空间以避免局部最优。定位潜在解后，金豺聚焦优化解空间中最有前景的区域，类似于向猎物位置聚集。金豺群体的等级结构影响决策过程，高阶金豺基于过往成功经验引导搜索方向。

GJO在特征选择、工程设计和多目标优化等问题中表现出有效性。其性能常与PSO和遗传算法（GA）等元启发式算法对比，在收敛速度和求解精度平衡上展示出竞争力。

GJO的数学模型可表示为：

$${\mathbf{X}}_{t+1}={\mathbf{X}}_t+\alpha \cdot (\text{Rand}\left({\mathbf{L}}_{\text{best}}-{\mathbf{X}}_t\right)+(1-\text{Rand})\left({\mathbf{G}}_{\text{best}}-{\mathbf{X}}_t\right))$$

其中：X_t为迭代t时金豺的当前位置，α为影响移动步长的控制参数，Rand为0-1随机数，L_best和G_best分别表示局部和全局最优解。

Yuan等（2022a）通过集成Gold-SA和动态透镜成像学习提出混合GJO（LSGJO）。新的更新规则和缩放因子提升了种群多样性，避免局部最优。LSGJO在基准函数和实际设计问题中优于其他算法，收敛更快更准。实验结果表明LSGJO优于11种前沿优化算法，实现了更快更精确的收敛。该算法显著增强了全局和局部搜索能力，擅长解决复杂约束问题。Rezaie等（2022）采用基于PSO的GJO方法最小化PEMFC堆实测与仿真输出电压的均方误差（SSE）。该方法在两个案例中验证并与多种最新优化器对比，表明ICSO在估计最优PEMFC模型中性能优越。针对GJO存在的利用能力弱、易陷局部最优和探索-利用平衡问题，Mohapatra & Mohapatra（2023）提出快速反向学习GJO（FROBL-GJO），通过反向学习技术提升精度和收敛速度。在CEC基准和实际问题上的测试表明，FROBL-GJO优于其他方法，证明其在全局优化和工程设计中的有效性。

3.19. 蜣螂优化算法

蜣螂优化算法（Dung Beetle Optimizer, DBO）受蜣螂滚动行为启发（Xue & Shen，2023），涉及寻找和运输粪便筑巢。蜣螂通过导航和最优方向滚动粪球展示智能觅食策略。DBO模拟该行为，通过定向移动和随机扰动平衡探索与利用。解的移动更新为：

$$X_i(t+1)=X_{\text{best}}(t)+A\cdot D\text{\hspace{1em}(47)}$$

其中X_best(t)为迭代t时最优解位置，A为控制移动方向的系数，D表示蜣螂与最优解的距离。移动系数A更新以平衡探索与利用：

$$A=2\cdot a\cdot r-a\text{\hspace{1em}(48)}$$

其中：a为随时间递减以促进收敛的参数，r为0-1随机数。

距离D计算为：

$$D=\left|C\cdot X_{\text{best}}(t)-X_i(t)\right|\text{\hspace{1em}(49)}$$

其中C为另一控制距离的系数，计算为：

$$C=2\cdot r\text{\hspace{1em}(50)}$$

DBO通过自适应控制参数A和C平衡探索与利用，初始探索搜索空间，后期聚焦利用。随迭代推进，a值递减促进向最优解收敛：

$$a(t)=2-\frac{t}{T}\text{\hspace{1em}(51)}$$

其中t为当前迭代，T为最大迭代次数。

Duan等（2023）提出了一种结合ARIMA模型（处理线性分量）和CNN-LSTM模型（处理非线性分量）的空气质量指数（AQI）预测组合模型，超参数通过DBO优化。该模型在四个城市的真实数据上优于九种常用模型。Shen等（2023）提出多策略增强DBO（MDBO），通过动态Beta分布反射解、Lévy分布管理越界粒子和两种交叉算子改进原始DBO的全局搜索能力和局部最优规避，提升了收敛性和探索-利用平衡。Jaiswal等（2023）提出DBO解决含太阳能和风电的最优潮流（OPF）问题。针对这些能源的随机特性，DBO利用对数正态和威布尔概率密度函数估计风光发电量。DBO在标准和改进IEEE 30节点系统上的MATLAB实现及与多种优化方法的对比分析，展示了其在复杂电力系统挑战中的可靠性和有效性。

3.20. 长鼻浣熊优化算法

长鼻浣熊优化算法（Coati Optimization Algorithm, COA）受长鼻浣熊（小型杂食性哺乳动物，以协作行为和智能解决问题能力著称）的社会觅食与移动模式启发（Dehghani等，2023a）。COA包含探索和利用两个关键阶段，由长鼻浣熊的社会等级和觅食习性主导。探索阶段，长鼻浣熊移动以发现搜索空间新区域（见图12群体攻击树上鬣蜥与另一半捕猎落地鬣蜥）。

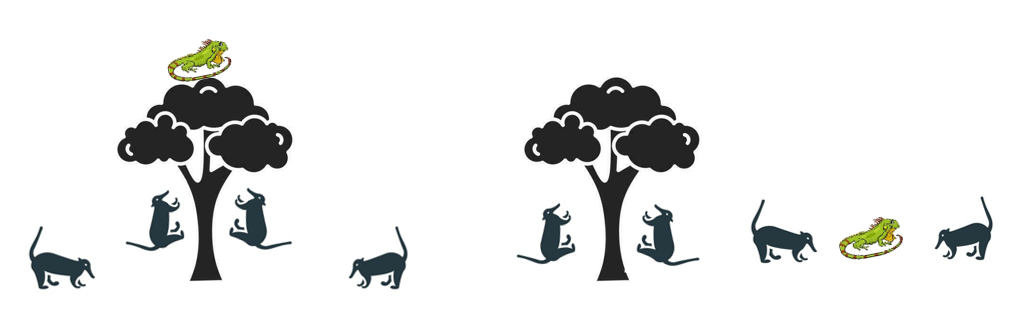
其移动模型为：

$$X_i(t+1)=X_i(t)+\beta \cdot \left(X_{\text{leader}}(t)-X_i(t)\right)+\alpha \cdot \text{randn}(0,1)\text{\hspace{1em}(52)}$$

其中X_leader(t)为迭代t时长鼻浣熊领导者位置，β控制领导者影响，α为添加随机扰动以促进探索的系数，randn(0,1)为正态分布随机数。利用阶段，长鼻浣熊聚焦微调最优已知解周围位置，每只长鼻浣熊位置更新为：

$$X_i(t+1)=X_i(t)+\gamma \cdot \left(X_{\text{best}}(t)-X_i(t)\right)\text{\hspace{1em}(53)}$$

其中X_best(t)为当前最优解，γ为控制向最优解步长的参数。COA采用自适应行为机制，随时间调整β、α和γ等参数以平衡探索与利用，自适应机制公式为：

$$\gamma (t)={\gamma }_{\min }+\left({\gamma }_{\max }-{\gamma }_{\min }\right)\cdot \frac{t}{T}\text{\hspace{1em}(54)}$$

其中γ_min和γ_max定义利用参数范围，t为当前迭代，T为总迭代次数。

Hashim等（2023a）提出动态COA（DCOA）作为特征选择技术，迭代过程中动态引入不同特征。DCOA通过动态反向候选解增强探索与利用能力，无需预参数调整。在CEC’22测试集和九个医疗数据集上的评估表明，DCOA优于七种知名元启发式算法，统计测试确认其整体准确率89.7%、特征选择率24%、灵敏度93.35%、特异度96.81%、精度93.90%。Bas & Yildizdan（2023）提出增强COA（ECOA），通过两项修改在搜索中保持种群多样性。在多种测试组中的评估表明，ECOA在23个经典CEC函数、CEC-2017和CEC-2020函数（5、10、30维）及大数据优化问题（BOP，300、500、1000周期）中优于COA。统计测试确认ECOA优于COA和七种最新算法，成为连续优化问题的有力替代。Hashim等（2023a）提出改进COA（mCoatiOA），通过集成自适应s-最优变异、定向变异和向全局最优的搜索方向控制增强原始算法。在CEC’20测试集和UCI仓库15个基准数据集上与多种优化算法的对比测试表明，mCoatiOA在75%的数据集上取得最佳结果，平均适应度和标准差显著提升。

3.21 混沌博弈优化算法

混沌博弈优化算法（CGO）是一种受混沌博弈概念启发的元启发式算法。在混沌博弈中，一个点通过迭代向分形结构中随机选择的顶点靠近，生成覆盖分形吸引子的模式（Talatahari & Azizi, 2021）。

CGO首先在可行搜索空间内随机初始化一组点 ${\mathbf{x}}_i$：

$${\mathbf{x}}_i={\mathbf{x}}_{\min }+\text{rand}\left({\mathbf{x}}_{\max }-{\mathbf{x}}_{\min }\right)$$

其中 ${\mathbf{x}}_{\min }$ 和 ${\mathbf{x}}_{\max }$分别定义搜索空间的上下界，rand是生成[0,1]区间随机数的函数。

CGO的位置更新规则依赖于目标点 $\mathbf{g}$ 和混沌映射的使用。设 $\mathbf{g}$ 为从当前种群或历史最优解中随机选择的点，每个解 ${\mathbf{x}}_i$ 的新位置更新如下：

$${\mathbf{x}}_i^{(t+1)}={\mathbf{x}}_i^{(t)}+\beta (\mathbf{g}-{\mathbf{x}}_i^{(t)})$$

其中 $\beta$ 是决定步长的缩放因子，可基于混沌映射调整。常用的混沌映射是逻辑映射：

$${\beta }_{t+1}=r{\beta }_t\left(1-{\beta }_t\right)$$

其中 $r$ 为参数（通常取 $r=4$ 以产生混沌行为），且 $\beta \in (0,1)$。

算法迭代直至满足终止准则（如最大迭代次数 $T$ 或最优解变化小于预定义阈值 $ϵ$）：

$$\Vert {\mathbf{x}}_{\text{best}}^{(t+1)}-{\mathbf{x}}_{\text{best}}^{(t)}\Vert <ϵ$$

CGO利用混沌行为和分形特性探索搜索空间并向最优解收敛。混沌映射增强了多样性并有助于逃离局部最优。

Talatahari & Azizi (2020) 在34个带约束的基准数学问题和15个工程设计问题上测试了CGO算法。通过最小值、均值、最大值和标准差等统计量，将结果与其他标准、改进及混合元启发式算法对比，CGO在多数情况下表现更优。Khodadadi等（2023a）提出多目标CGO（MOCGO），通过固定大小的外部存档存储帕累托最优解，并引入领导者选择机制处理多目标优化问题。该算法利用CGO的混沌理论和分形模型，应用于8个多目标工程设计问题。通过CEC-09、ZDT和DTLZ等17个案例研究，并与6种知名多目标算法对比4种性能指标，结果表明MOCGO在帕累托最优解的收敛性和覆盖性上表现更优。Ramadan等（2021）将CGO用于估计三二极管（TD）光伏（PV）模型的未知参数，该模型对提升光伏系统仿真精度至关重要。由于光伏电池数据手册中参数信息不全且模型高度非线性，基于CGO的方法用于在不同温度和辐照条件下估计真实光伏电池及组件参数。仿真结果与实验数据对比验证了模型精度，CGO在均方根误差（RMSE）、均值、标准差和执行时间上均优于现有方法。

3.22 白鲸优化算法

白鲸优化算法（BWO）是一种受白鲸捕猎和迁徙行为启发的元启发式算法。通过模拟白鲸独特的螺旋形捕猎路径和集体迁徙行为，BWO平衡了探索与开发，并随时间调整参数以高效收敛至最优解。算法初始时将白鲸随机分布于搜索空间。BWO的核心特征是模拟捕猎行为的螺旋路径：

$$X_i(t+1)=X_{\text{best}}(t)+D\cdot e^{b\cdot l}\cdot \cos (2\pi l)\text{\hspace{1em}(55)}$$

其中 ( X_{\text{best}}(t) ) 为t时刻最优解位置，( D ) 为白鲸与猎物的距离，( b ) 控制螺旋紧密度，( l ) 为决定螺旋形状的随机变量。白鲸的集体迁徙影响算法的开发阶段，每头白鲸基于当前位置和群体最优位置调整：

$$X_i(t+1)=X_{\text{best}}(t)+C\cdot (X_{\text{best}}(t)-X_i(t))\text{\hspace{1em}(56)}$$

其中 ( C ) 控制向最优解的吸引力系数，( X_{\text{best}}(t) ) 为t时刻最优白鲸位置，( X_{i}(t) ) 为i号白鲸当前位置。BWO通过自适应参数平衡探索与开发：随迭代进行，螺旋路径变紧，向最优解的吸引力增强：

$$b(t)=b_{\min }+\left(b_{\max }-b_{\min }\right)\cdot \left(1-\frac{t}{T}\right)\text{\hspace{1em}(57)}$$

其中 ( b(t) ) 随迭代次数 ( t ) 增加而减小，( T ) 为总迭代次数。

Li等（2024）提出基于改进BWO（IBWO）的分布式发电（DG）多目标分层优化规划模型，考虑了以往研究常忽略的DG输出不确定性和需求响应。IBWO使年综合成本、电压偏差和功率损耗分别降低11.66%、40.55%和38.61%，提升了电能质量和经济效益。Hussien等（2023）提出改进BWO（mBWO），通过精英进化、随机化控制和过渡因子解决原算法早熟收敛和探索-开发失衡问题。在29个CEC2017函数和8个工程问题上，mBWO优于原BWO和10种其他优化器。Houssein & Sayed（2023）通过反向学习（OBL）和动态候选解（DCS）结合k近邻（kNN）分类器改进BWO多样性和早熟问题，改进的OBWOD算法在CEC’22基准和10个医疗数据集上以85.17%的分类准确率优于7种算法。

3.23 瞪羚优化算法

瞪羚优化算法（GOA）受瞪羚野外行为启发，尤其是其快速自适应移动、急转和加速避敌的能力（Agushaka等，2023）。该算法模拟瞪羚动态策略平衡探索与开发，通过调整运动模式优化搜索。每个瞪羚位置基于种群最优位置更新，采用受瞪羚动力学启发的自适应运动策略，位置更新方程为：

$$X_i(t+1)=X_{\text{best}}(t)+V_i(t)+\alpha \cdot \left(X_{\text{best}}(t)-X_i(t)\right)\text{\hspace{1em}(58)}$$

其中：$X_{\text{best}}(t)$ 为t次迭代最优位置，$V_i(t)$ 为t次迭代瞪羚速度，$\alpha$ 控制向最优位置的吸引力强度。为平衡探索与开发，瞪羚速度更新受当前位置与最优位置差异影响：

$$V_i(t+1)=\beta \cdot V_i(t)+\gamma \cdot \left(X_{\text{best}}(t)-X_i(t)\right)+\delta \cdot \left(X_{\text{rand}}(t)-X_i(t)\right)\text{\hspace{1em}(59)}$$

其中：$\beta$ 控制速度惯性，$\gamma$ 影响向最优位置的吸引力，$\delta$ 控制随机解 $X_{\text{rand}}(t)$ 对多样性的维持。参数 $\alpha$、$\beta$、$\gamma$ 随优化过程动态调整以平衡探索与开发，通常随时间递减以先探索后开发：

$$\alpha (t)={\alpha }_{\max }-\frac{t}{T}\cdot \left({\alpha }_{\max }-{\alpha }_{\min }\right)\text{\hspace{1em}(60)}$$

$$\beta (t)={\beta }_{\max }-\frac{t}{T}\cdot \left({\beta }_{\max }-{\beta }_{\min }\right)\text{\hspace{1em}(61)}$$

其中：$t$ 为当前迭代，$T$ 为总迭代次数。随迭代推进，瞪羚逐渐向最优解聚集，随机探索减少，最终收敛至最优解并保持多样性：

$$X_{\text{best}}(t+1)=X_{\text{best}}(t)+\epsilon \cdot \left(X_{\text{best}}(t)-X_{\text{mean}}(t)\right)\text{\hspace{1em}(62)}$$

其中：$X_{\text{mean}}(t)$ 为t次迭代所有瞪羚平均位置，$\epsilon$ 控制平均位置对最优解的影响。

Khodadadi等（2023b）提出山地瞪羚优化（MGO）作为结构工程中桁架结构优化的新型元启发式算法，受瞪羚社会行为启发，用于处理多局部最优和非凸搜索空间的复杂约束设计问题，相比传统方法提供更优轻量化设计。Mehta等（2024）将MGO与神经网络结合优化车辆部件等机械系统，通过混合MGO与Nelder-Mead算法（HMGO-NM）处理汽车、制造、建筑和机械工程任务，对比结果显示HMGO-NM的优越性。Abdel-Salam等（2024）提出自适应混沌动态GOA（ACD-GOA），通过动态反向学习、自适应惯性权重和精英策略提升特征选择（FS）效率和收敛速度。在12个CEC2022函数和14个FS基准上，ACD-GOA用K-NN分类器实现0.78-1.00的分类准确率，优于其他元启发式算法。

https://doi.org/10.48550/arXiv.2501.14769