洛谷 P1002 过河卒

诶，就是玩 (这是个传送门

题目描述

棋盘上 A 点有一个过河卒，需要走到目标 B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，A 点 (0, 0)、B 点 (n,m)，同样马的位置坐标是需要给出的。

现在要求你计算出卒从 A 点能够到达 B 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 B 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

输入输出样例

输入 #1

6 6 3 3

输出 #1

6

说明/提示

对于 100% 的数据，1 ≤n,m≤20，0 ≤ 马的坐标 ≤20。

 

解：

看到题目的第一眼，有障碍物，需要寻找路径，这不贴个板子，上手dfs（然后就wa了，这说明数据范围很重要。

ps:dfs的行列≤15；

所以我们要换种思路（看来懒一下都不行~

因为每一个点都只能由上边和左边的点的次数相加得到，所以我们很快可以想到动态规划（dp，如果你会的话

                                                   状态转移方程为：dp[i][j] = max(dp[i-1][j] + dp[i][j-1] , dp[i][j]) 

我们来模拟一下示例：

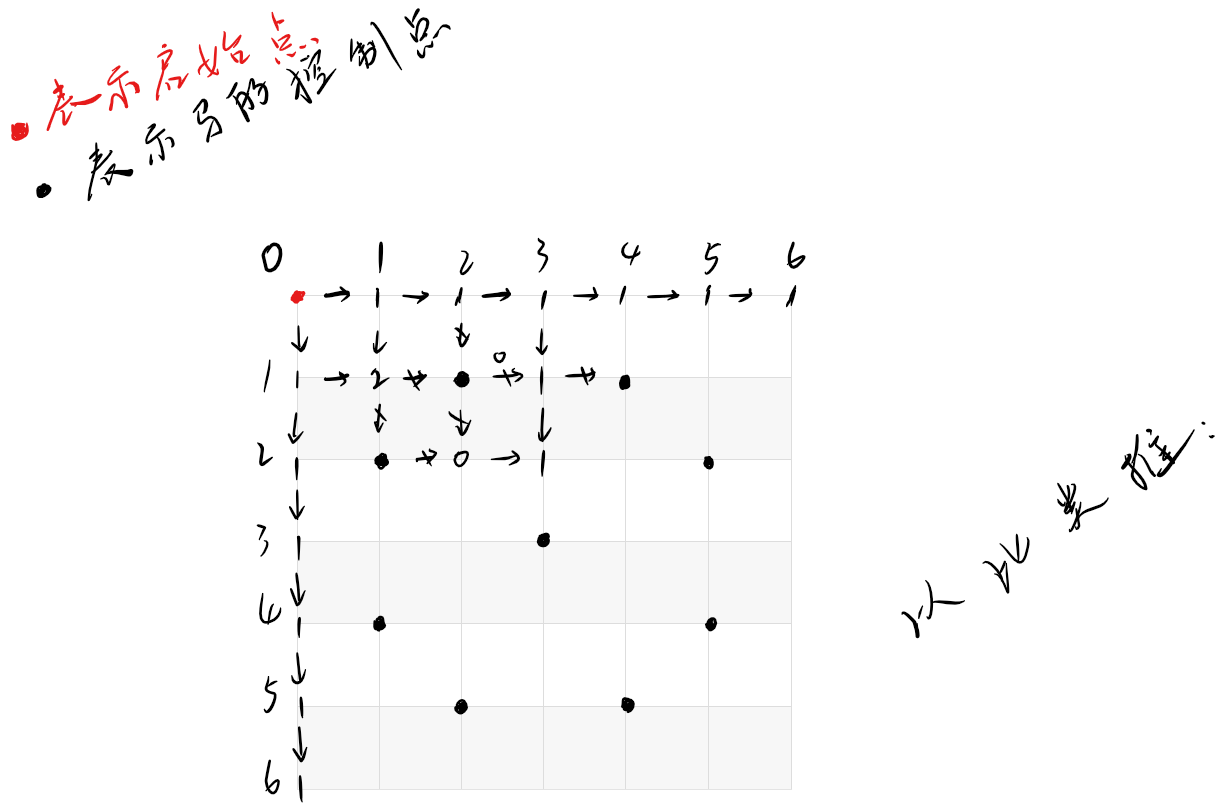
最后运行的结果应该为：

dp的过程就是这样（很简单的过程吧  

然后就开始上手吧，值得一提的是（为了减少特判，我们以（2，2）作为起始点可以减少特判  

下面是AC代码：

#include<bits/stdc++.h>
#define sc(x) scanf("%lld", &(x))
#define pr(x) printf("%lld\n", (x))
#define rep(i, l, r) for (int i = l; i <= r; ++i)
using namespace std;
typedef long long ll;
const int N = 1e5 + 7;
const int mod = 1e9 + 7;	
ll dp[25][25] ;
int dir[][2] = {{-2,-1},{-1,-2},{1,-2},{2,-1},{-1,2},{-2,1},{1,2},{2,1}} ;
void jiushiwan(int x,int y){
	for(int i = 0;i < 8;i ++) dp[x+dir[i][0]][y+dir[i][1]] = -1 ;
	dp[2][2] = 1 ;dp[x][y] = -1 ;
}
int main(){
	//freopen("in.txt", "r", stdin);
	//freopen("test.txt", "w", stdout);
	memset(dp,0,sizeof(dp)) ;
	int xa,ya,xb,yb ;cin >> xa >> ya >> xb >> yb ;
	jiushiwan(xb+2,yb+2) ;
	for(int i = 1;i <= xa+2;i ++){
		for(int j = 1;j <= ya+2;j ++){
			if(dp[i][j]==-1) dp[i][j] = 0 ;
			else dp[i][j] = max(dp[i-1][j] + dp[i][j-1] , dp[i][j]) ;
		}
	}
	cout << dp[xa+2][ya+2] << endl ;
	// for(int i = 2;i <= xa+2;i ++){
	// 	for(int j = 2;j <= ya+2;j ++){
	// 		cout << dp[i][j] << " " ;
	// 	}
	// 	cout << endl ;
	// }
	return 0;
} 

让我来强行解释一波（毕竟水平有限，写的实在是不规范不美观：

//1.
for(int i = 2;i <= xa+2;i ++)
		for(int j = 2;j <= ya+2;j ++) //+2 防越界，减特判

//啊？为什么从1开始不从0开始?->（i-1,j-1越界了
//你的初始位置是(2,2)那为什么不从(2,2)开始呢？->为了减少特判特殊情况，会存在马的控制点小于2
//从2开始的dp结果,注意看前两行'#'为起始错误数据（包括0，1列行
//0    0    0    0    0   -1    0   -1    0  dp[1][4]未置0，导致下一级dp错误
//0    0    0    0   -1    0    0    0   -1
//0    0    1    1   #0    0   *0    0    0
//0    0    1    2    0    0    0    0    0
//0    0    1    3    3    0    0    0    0
//0    0    1    4    7    7    7    7    7
//0    0    1    5   12   19   26   33   40
//0    0    1    6   18   37   63   96  136
//0    0    1    7   25   62  125  221  357
//0    0    1    8   33   95  220  441  798
//0    0    1    9   42  137  357  798 1596 -> 1617

//2.
for(int i = 0;i <= xa+2;i ++){
		for(int j = 0;j <= ya+2;j ++){
			printf("%5d",dp[i][j]) ;
		}
		cout << endl ;
	}

//用来检测矩阵的dp情况

//3.
void jiushiwan(int x,int y){
	for(int i = 0;i < 8;i ++) dp[x+dir[i][0]][y+dir[i][1]] = -1 ;
	dp[2][2] = 1 ;dp[x][y] = -1 ;
}

//用来记录马的控制点，纪录和对起始点的初始化的顺序问题我们等下用示例解决

eg1：

输入：

4 8 2 4 //图

输出：

0
//    1    1    1    0    0    0    0    0    0
//    1    2    0    0    0    0    0    0    0
//    1    3    3    3    0    0    0    0    0
//    1    4    0    3    3    3    0    0    0
//    1    5    5    0    3    0    0    0    0

eg2:

输入：

8 6 0 4 //#1

输出：

1617 //#1
//    1    1    1    1    0    0    0
//    1    2    0    1    1    1    0
//    1    3    3    0    1    0    0
//    1    4    7    7    8    8    8
//    1    5   12   19   27   35   43
//    1    6   18   37   64   99  142
//    1    7   25   62  126  225  367
//    1    8   33   95  221  446  813
//    1    9   42  137  358  804 1617

eg3:（关于dp[2][2]的初始化和马的控制点纪录顺序问题，虽然咱也觉得不符合常理

输入：

6 6 1 2 //你会发现，初始点是马的控制点

输出：

36 //初始化dp[2][2]在纪录后
//    1    1    1    1    0    0    0
//    1    2    0    1    1    1    1
//    0    2    2    3    0    1    2
//    0    0    2    0    0    1    3
//    0    0    2    2    2    3    6
//    0    0    2    4    6    9   15
//    0    0    2    6   12   21   36

0  //初始化dp[2][2]在纪录前
//    0    0    0    0    0    0    0
//    0    0    0    0    0    0    0
//    0    0    0    0    0    0    0
//    0    0    0    0    0    0    0
//    0    0    0    0    0    0    0
//    0    0    0    0    0    0    0
//    0    0    0    0    0    0    0

over！（便于复习二维dp