1最短加法链问题
1.1问题定义
给定一个正整数和一个实数,我们面临着如何用最少的乘法次数计算出这个正整数的问题。例如,计算![]() 可以通过 6 次乘法逐步实现:
可以通过 6 次乘法逐步实现: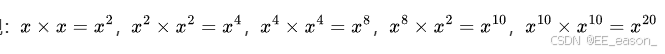 。
。![]() 经过证明,这种方式确实是计算最少需要的 6 次乘法。在这个计算过程中,幂序列中各次组成了正整数的一个加法链,如对于整数 23,3、5、10、20、23 就组成了一个加法链。
经过证明,这种方式确实是计算最少需要的 6 次乘法。在这个计算过程中,幂序列中各次组成了正整数的一个加法链,如对于整数 23,3、5、10、20、23 就组成了一个加法链。
1.2动态规划解决方法
- 定义状态:设
dp[i]表示正整数i的最短加法链长度。 - 状态转移方程:对于正整数
i,遍历小于i的正整数j和k,如果i = j + k,则dp[i] = min(dp[i], dp[j] + 1)。 - 初始状态:
dp[1] = 1。 - 通过这种方式,逐步计算出较大正整数的最短加法链长度。
1.3动态规划代码
def add_chain(n):
dp = [float('inf')] * (n + 1)
dp[1] = 1
for i in range(2, n + 1):
for j in range(1, i):
for k in range(1, j + 1):
if j + k == i:
dp[i] = min(dp[i], dp[j] + 1)
return dp[n]
n = 10
print(add_chain(n))
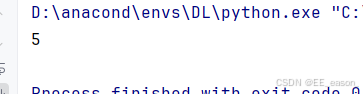
结果:测试n为10时输出5是正确的
2盒子里的气球问题
2.1问题定义
- 首先明确问题的目标是找到一种放置气球的顺序,使得放置完毕后所有气球占据的总体积最大。
- 由于气球会一直膨胀直到接触到其他气球或盒子的边界,并且必须等一个气球扩展完毕才能扩展下一个气球,所以放置气球的顺序会直接影响最终的总体积。
2.2贪心算法解决方法
- 初始化总体积为 0。
- 遍历所有未放置气球的点,对于每个点,计算如果在这个点放置气球后,气球膨胀到接触其他气球或盒子边界时所占据的体积增量。
- 选择体积增量最大的点放置气球,并更新总体积。
- 重复上述步骤,直到所有点都放置了气球。
2.3贪心算法代码
from itertools import permutations
import math
def get_maximum_volume(box_dims, points_list):
max_balloon_volume = 0
optimal_order = []
for point_order in permutations(points_list):
total_volume = 0
occupied_coords = set()
for point in point_order:
px, py, pz = point
max_radius = min(
px, box_dims[0] - px,
py, box_dims[1] - py,
pz, box_dims[2] - pz
)
radius = 0
for r in range(int(max_radius), 0, -1):
if not any((px + dx, py + dy, pz + dz) in occupied_coords
for dx in range(-r, r + 1)
for dy in range(-r, r + 1)
for dz in range(-r, r + 1)
if dx ** 2 + dy ** 2 + dz ** 2 <= r ** 2):
radius = r
break
if radius > 0:
volume = (4 / 3) * math.pi * (radius ** 3)
total_volume += volume
for dx in range(-radius, radius + 1):
for dy in range(-radius, radius + 1):
for dz in range(-radius, radius + 1):
if dx ** 2 + dy ** 2 + dz ** 2 <= radius ** 2:
occupied_coords.add((px + dx, py + dy, pz + dz))
if total_volume > max_balloon_volume:
max_balloon_volume = total_volume
optimal_order = point_order
return max_balloon_volume, optimal_order
box_dims = (15, 15, 15)
points_list = [(2, 2, 2), (12, 12, 12), (7, 7, 7), (10, 10, 5)]
max_volume, best_arrangement = get_maximum_volume(box_dims, points_list)
print("Max Volume:", max_volume)
print("Best Arrangement:", best_arrangement)
测试长方体参数:

结果:
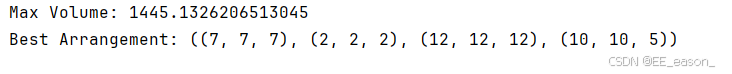





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








