【网络流24题-16】数字梯形问题

【问题描述】： 
　　给定一个由 n 行数字组成的数字梯形如下图所示。梯形的第一行有 m 个数字。从梯形的顶部的 m 个数字开始，在每个数字处可以沿左下或右下方向移动，形成一条从梯形的顶至底的路径。 
　　规则1：从梯形的顶至底的m条路径互不相交。 
　　规则2：从梯形的顶至底的m条路径仅在数字结点处相交。 
　　规则3：从梯形的顶至底的m条路径允许在数字结点相交或边相交。 
　　
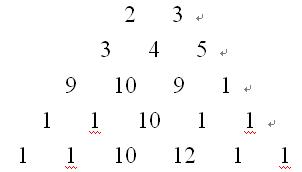
【编程任务】：

　　对于给定的数字梯形，分别按照规则1，规则2，和规则 3 计算出从梯形的顶至底的 m条路径，使这 m条路径经过的数字总和最大。 

plan1:   拆点，原点a与新点a'之间连一条流量1费用为数字的边，上层点b'向下层点a连一条流量1费用0的边，超级汇点S向第一层连边，最下面一层向T连边（流量1费用0），跑最大费用流。

plan2:  可以相交，就说明点可以重复访问，a与a'之间连边流量改为INF就行了，其余同plan1相同。

plan3:  就是从第一层每个点跑到T的最长路的和，为了方便，直接将与S或T不关联的边流量改为INF就行了。

贴代码

#include<iostream>
#include<cmath>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<cstring>
#include<ctime>
#include<queue>
#include<map>
using namespace std;
const int N=1605;
int n,m,a,b,c,d,e,cnt,S,T,full,k;
int inside[N],dist[N],times[N];
int fa[N][2],ans=0,mem[45][45];
struct sss{int to,flow,cost,op;};
vector <sss> Map[N];
struct node{int f,g,to;};
inline int read()
{
	char t;int u=0,k=1;t=getchar();
	while(t<'0'||t>'9'){if(t=='-')k=-1;t=getchar();}
	while(t>='0'&&t<='9'){u=u*10+t-'0';t=getchar();}
	return u*k;
}
inline void link(int a,int b,int c,int d)
{
	Map[a].push_back((sss){b,c,d,Map[b].size()});
	Map[b].push_back((sss){a,0,-d,Map[a].size()-1});
}
inline bool Spfa(int S,int T,int fan)
{
	memset(inside,0,sizeof(inside));
	for(int i=1;i<=full;i++)dist[i]=0xfffffff*fan;
	queue <int> que;
	que.push(S);dist[S]=0;
	while(!que.empty())
	{
		int a=que.front();que.pop();inside[a]=0;
		if(Map[a].size())for(int i=0;i<Map[a].size();i++)
		{
			int b=Map[a][i].to,c=Map[a][i].cost;
			if((dist[a]+c)*fan<dist[b]*fan&&Map[a][i].flow)
			{
				dist[b]=dist[a]+c;
				fa[b][0]=a;fa[b][1]=i;
				if(!inside[b]){inside[b]=1;que.push(b);}
			}
		}
	}
	return dist[T]!=0xfffffff*fan;
}
inline void add()
{
	int u=T,delta=0xfffffff;
	while(u!=S)
	{
		delta=min(delta,Map[fa[u][0]][fa[u][1]].flow);
		u=fa[u][0];
	}
	ans+=delta*dist[T];
	u=T;
	while(u!=S)
	{
		Map[fa[u][0]][fa[u][1]].flow-=delta;
		Map[u][Map[fa[u][0]][fa[u][1]].op].flow+=delta;
		u=fa[u][0];
	}
}
int main()
{
	m=read();n=read();e=(m+m+n-1)*n/2;S=e*2+1;T=S+1;full=T;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m+i-1;j++)
			mem[i][j]=read();

//part 1：

	for(int i=1;i<=m;i++)link(S,i,1,0);
	for(int i=1;i<=n-1;i++)
		for(int j=1;j<=m+i-1;j++)
		{
			int u=(m+m+i-2)*(i-1)/2+j;
			link(u+e,u+m+i-1,1,0);link(u+e,u+m+i,1,0);
			link(u,u+e,1,mem[i][j]);
		}
	for(int i=e-n-m+2;i<=e;i++)link(i,i+e,1,mem[n][i+n+m-e-1]),link(i+e,T,1,0);
	while(Spfa(S,T,-1))add();cout<<ans<<"\n";

//part 2：

	memset(Map,0,sizeof(Map));ans=0;full=e+2;S=e+1;T=e+2;
	for(int i=1;i<=m;i++)link(S,i,1,mem[1][i]);
	for(int i=1;i<=n-1;i++)
		for(int j=1;j<=m+i-1;j++)
		{
			int u=(m+m+i-2)*(i-1)/2+j;
			link(u,u+m+i-1,1,mem[i+1][j]);link(u,u+m+i,1,mem[i+1][j+1]);
		}
	for(int i=e-n-m+2;i<=e;i++)link(i,T,23333,0);
	while(Spfa(S,T,-1))add();cout<<ans<<"\n";
	memset(Map,0,sizeof(Map));ans=0;S=e+1;T=e+2;full=T;

//part 3：

	for(int i=1;i<=m;i++)link(S,i,1,mem[1][i]);
	for(int i=1;i<=n-1;i++)
		for(int j=1;j<=m+i-1;j++)
		{
			int u=(m+m+i-2)*(i-1)/2+j;
			link(u,u+m+i-1,23333,mem[i+1][j]);link(u,u+m+i,23333,mem[i+1][j+1]);
		}
	for(int i=e-n-m+2;i<=e;i++)link(i,T,23333,0);
	while(Spfa(S,T,-1))add();cout<<ans<<"\n";
	return 0;
}