遗传算法及MATLAB代码实现（一）

DukeCheung

已于 2024-09-19 16:16:12 修改

阅读量4.4k

点赞数 41

CC 4.0 BY-SA版权

文章标签： matlab

于 2024-09-19 16:04:39 首次发布

本文链接：https://blog.youkuaiyun.com/DukeCheung/article/details/142261308

叠个Buff:博文仅供自己学习，如有错误，以你为准！

0.问题引入

求函数f(x)=11sin(6x)+7cos(5x),x∈[-π，π]的最大值点。

clear all
clc
%% 函数f(x)=11sin(6x)+7cos(5x),x∈[-pi,pi]
%绘制函数图像
x = (-pi) : 0.01 : pi;
[a, b] = size(x);
for i = 1:b
    y(i) = 11*sin(6*x(i))+7*cos(5*x(i));
end
plot(x, y, 'r')
title('函数曲线图')
xlabel('x')
ylabel('f(x)')

图像如下图所示：
f(x)的图像
下面我们用遗传算法来求解吧！

1. 遗传算法原理

生物进化
自然界“物竞天择，适者生存”，从某种程度上来讲，现存的生物就是自然界的最优解。为了找到最优的解，生物已经进化了无数代。进化靠什么，遗传和变异。
在这里插入图片描述

2.遗传算法步骤

2.1 编码

目的：将问题的可行解，抽象为适用于遗传算法的形式。
方法：二进制编码，将数值转为二进制串，用以求解问题。用二进制串表示十进制
例子：求解区间为[1,10],求解精度为1e-5
编码
一个长度为2的串能表示几个数呢？
区间区间范围为[1,10]，长度为2 的串提供的精度为多少？
对应精度为 $\frac{10-1}{2^{2}-1 } =3$
于是数值区间长度为L，精度为E的条件下，二进制串的长度n，三者关系为 $\frac{L}{2^{n}-1}\le E$
要想达到1e-5的精度，对于区间[1,10]，串应该满足什么条件呢？
$\frac{10-1}{2^{n}-1} \le 0.00001$ ，则 $n\ge20$
解码
二进制串的索引：就是在问当前串是第几个串。可以使用二进制转十进制得到。
以[1,0]为例，其十进制转换结果为02^0 + 1 * 2^1 = 2，
对应表示的数值为：7 = 1 + 2 * 3

以[1,1]为例，其十进制转换结果为12^0 + 1 * 2^1 = 3.
对应表示的数值为：10 = 1 + 3 * 3
一般的，区间范围为[a,b]，区间长度为L，即L = b –a ，串长为n，当前串对应十进制为T，则该串对
应实值解为：
$X=a+T\frac{b-a}{2^{n}-1}$
解释：如引例所示x∈[-π，π]，要先编码将 [-π，π]进行二进制编码，以便后续复制、交叉、变异操作。要判断f(x)的大小，需要将二进制编码解码，带入目标方程，计算其大小（适应值）。

2.2 初始化

也就是在自变量范围内随机产生初始值。初始种群个数为m个，那就产生m个随机化的初始解。
这个解在自变量范围内越分散越好。

2.3 适应度计算

如果求极值点，通常是求最小极值点；如果需要求最大值，加负号后求极小值值点即可。

2.4 复制

个体进行复制，以概率𝑝𝑐进行基因的交叉，注意复制交叉方式多种多样。
方法1：将个体适应度大小映射为概率进行复制：适应度高的个体有更大概率复制，且复制的份数
越多-轮盘赌法。
方法2：对适应度高的前N/4的个体进行复制，然后用这些个体把后N/4个体替换掉–精英产生精英

轮盘赌基本思想：适应度越高的解，按道理越应该高概率的进行复制，且复制的份数应该越多。
• 对于个体𝑥𝑖，计算对应适应度𝑓(𝑥𝑖)-> $p_{i}=\frac{f(x_{i})}{\sum_{f(x_{i})} }$
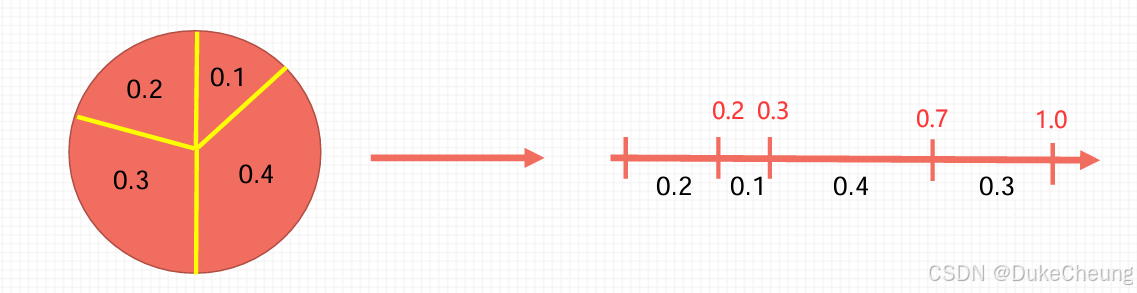
在这里插入图片描述
Rand = 0 ~ 0.2 ：表示对x1 复制
Rand = 0.2~0.3：表示对x2 复制
Rand = 0.3~0.7 ：表示对x3 复制
Rand = 0.7~1.0：表示对x4 复制

2.5 交叉

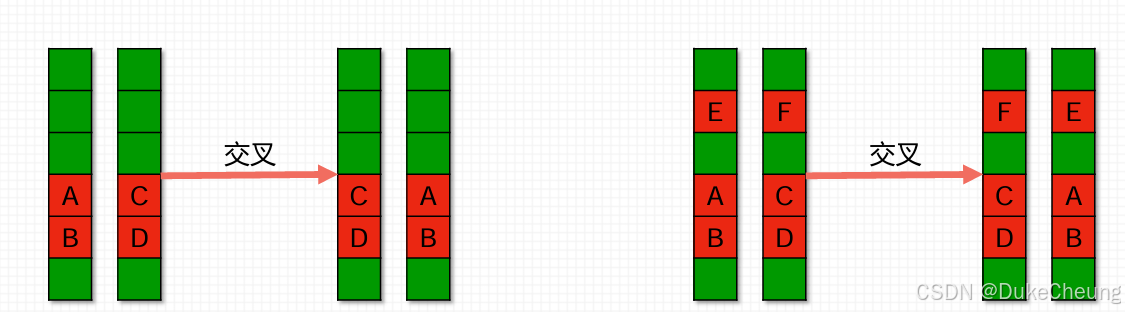
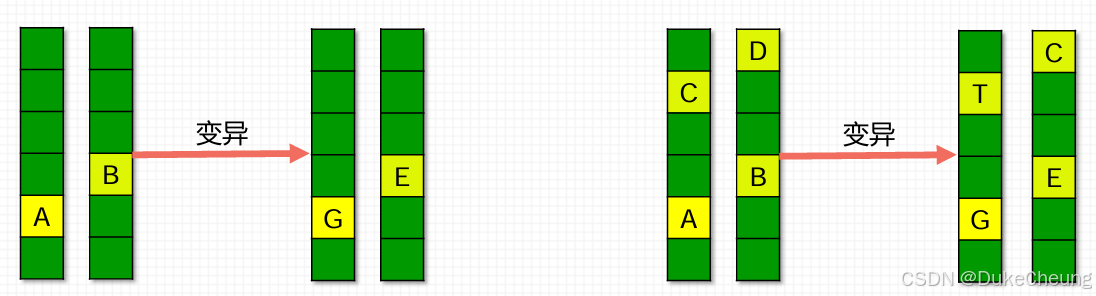
1和2,3和4，以一定概率决定是否交叉。若交叉，则二者选择随机一个段进行交叉。在这里插入图片描述

2.6 变异

按照一定概率决定该个体是否变异，若变异，随机选择一个位点进行变异：按位取反。
在这里插入图片描述

3.遗传算法的流程

遗传算法流程图

4.遗传算法编程

4.1 遗传算法求解极值点

开始求解引例

%主程序
popsize = 20;    %设置初始参数，群体大小
chromlength = 8;    %设置字符串长度，染色体长度
pc = 0.8;            %设置交叉概率
pm = 0.01;         %设置变异概率
pop = initpop(popsize, chromlength); %运行初始化函数，产生随机初始种群
for i = 1:400
[objvalue] = calobjvalue(pop);     %计算目标函数值
fitvalue = calfitvalue(objvalue);   %计算群体中每个个体的适应度
[newpop] = selection(pop, fitvalue);    %复制
[newpop] = crossover(pop,pc);        %交叉
[newpop] = mutation(pop, pm);       %变异
[bestindividual, bestfit] = best(pop,fitvalue); %求出群体中适应值最大的个体及其适应值
y(i) = max(bestfit);
n(i) = i;
pop5 = bestindividual;
x(i) = -pi+(2*pi).*decodechrom(pop5,1,chromlength)/255
pop = newpop;
end
fplot(@(x) 11*sin(6*x)+ 7*cos(5*x),[-pi,pi])
grid on
hold on
plot(x,y,'r*')
xlabel('自变量')
ylabel('目标函数值')
title('种群中的个体数目为20，二进制编码长度为8，交叉概率为0.7，变异概率为0.02')
fmax = max(y);
hold off


%初始化
function pop =initpop(popsize,chromlength)
pop = round(rand(popsize,chromlength))
%popsize表示群体的大小，chromlength表示染色体的长度
end


%计算目标函数值
%产生【2^n，2^(n-1)^,……,1】的行向量，然后求和，将二进制转化为十进制
function pop2 = decodebinary(pop)
[px,py] = size(pop)    %求pop行和列数
for i = 1:py
pop1(:,i) = 2.^(py-i).*pop(:,i);
end
pop2 = sum(pop1,2);     %求pop1的每行之和
end


%将二进制转化为十进制
function pop2 = decodechrom(pop,spoint,length)
pop1 = pop(:,spoint:spoint+length-1);
%取出第spoint位开始到第spoint+length-1位的参数
pop2 = decodebinary(pop1);
%利用上面函数decodebinary(pop)将用二进制的个体基因变为十进制
end

%实现目标函数的计算
function [objvalue] = calobjvalue(pop)
temp1 = decodechrom(pop,1,8)          %将pop每行转化为十进制
x = -pi + (2*pi).*temp1./255          %将二值域中的数转化为变量域的数
objvalue = 11*sin(6*x)+7*cos(5*x);    %计算目标函数值
end

%计算个体的适应值
function fitvalue = calfitvalue(objvalue)
global Cmin;
Cmin = 0;
[px, py] = size(objvalue);
for i =1:px
    if objvalue(i)+ Cmin > 0
        temp = Cmin +objvalue(i);
    else
        temp = 0.0;
    end
    fitvalue(i) = temp;
end
fitvalue = fitvalue';
end

%选择复制
function [newpop] =  selection(pop,fitvalue)
totalfit = sum(fitvalue);
fitvalue = fitvalue/totalfit;
fitvalue = cumsum(fitvalue); %如fitvalue=[1 2 3 4],则cumsum(fitvalue)=[1 3 6 10]
[px,py] = size(pop);
ms =sort(rand(px,1));
fitin = 1;
newin = 1;
while newin <= px
    if(ms(newin)) < fitvalue(fitin)
        newpop(newin,:) = pop(fitin, :);
        newin = newin + 1;
    else
        fitin = fitin + 1;
    end
end
end


%交叉
function [newpop] = crossover(pop, pc)
[px,py] = size(pop);
newpop = ones(size(pop));
for i = 1:2:px-1
    if(rand<pc)
        cpoint = round(rand*py);
        newpop(i,:) = [pop(i,1:cpoint),pop(i+1,cpoint+1:py)];
        newpop(i+1,:) = [pop(i+1,1:cpoint),pop(i,cpoint+1:py)];
    else
        newpop(i, :) = pop(i, :);
        newpop(i+1, :) = pop(i+1, :);
    end
end
end


%变异
function [newpop] = mutation(pop, pm)
[px, py] = size(pop);
newpop = ones(size(pop));
for i = 1:px
    if (rand<pm)
        mpoint = round(rand*py);   %产生的变异点在0-8之间,
        if mpoint <= 0
            mpoint = 1;               %变异位置
        end
        newpop(i, :) = pop(i,:);
        if any(newpop(i,mpoint)) == 0
            newpop(i, mpoint) = 1;
        else
            newpop(i, mpoint) = 0;
        end
    else
        newpop(i, :) = pop(i, :);
    end
end
end

%求出群体中最大的适应值及其个体
function [bestindividual, bestfit] = best(pop, fitvalue)
[px, py] = size(pop);
bestindividual = pop(1,:);
bestfit = fitvalue(1);
for i = 2:px
    if fitvalue(i) >bestfit
        bestindividual = pop(i, :);
        bestfit = fitvalue(i);
    end
end
end

结果：
在这里插入图片描述

4.2 遗传算法求解TSP问题

旅行商问题（TSP问题)。假设有一个旅行商人要拜访全国31个省会城市，他需要选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。对路径选择的要求是:所选路径的路程为所有路径之中的最小值。
全国31个省会城市的坐标为[1304 2312;36391315;4177 2244;37121399;34881535;33261556; 3238 1229;4196 1004;4312 790; 4386 570;3007 1970;25621756;2788 1491;2381 1676;1332 695;3715 1678;3918 2179;4061 2370;37802212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2367;3394 2643;34393201; 29353240;3140 3550; 2545 2357; 2778 2826;2370 2975]。

遗传算法求解TSP问题代码

%% 遗传算法解决TSP问题
clear all;
close all;
clc;
 
%% 初始化参数
C=[1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;...
    3238 1229;4196 1044;4312  790;4386  570;3007 1970;2562 1756;...
    2788 1491;2381 1676;1332  695;3715 1678;3918 2179;4061 2370;...
    3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2376;...
    3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;...
    2370 2975];                  %31个省会城市坐标
N=size(C,1);                     %TSP问题的规模,即城市数目
D=zeros(N);                      %任意两个城市距离间隔矩阵
 
%% 求任意两个城市距离间隔矩阵
for i=1:N
    for j=1:N
        D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
    end
end
NP=200;                           %免疫个体数目
G=1000;                           %最大免疫代数
f=zeros(NP,N);                    %用于存储种群
F = [];                           %种群更新中间存储
for i=1:NP
    f(i,:)=randperm(N);           %随机生成初始种群
end
R = f(1,:);                       %存储最优种群
len=zeros(NP,1);                  %存储路径长度
fitness = zeros(NP,1);            %存储归一化适应度值
gen = 0;
 
%% 遗传算法循环
while gen<G
    %% 计算路径长度
    for i=1:NP
        len(i,1)=D(f(i,N),f(i,1));                %最终位置和起点位置的距离，如路线为1-2-3，完整的距离为1-2-3-1
        for j=1:(N-1)
            len(i,1)=len(i,1)+D(f(i,j),f(i,j+1));
        end
    end
    maxlen = max(len); 
    minlen = min(len);
    
    %% 更新最短路径
    rr = find(len==minlen);
    R = f(rr(1,1),:);
    %R = f(rr,:);
    
    %% 计算归一化适应度
    for i =1:length(len)
        fitness(i,1) = (1-((len(i,1)-minlen)/(maxlen-minlen+0.001)));
    end
    
    %% 选择操作
    nn = 0;
    for i=1:NP
        if fitness(i,1)>=rand
            nn = nn+1;
            F(nn,:)=f(i,:);
        end
    end
    [aa,bb] = size(F);
    while aa<NP
        nnper = randperm(nn);
        A = F(nnper(1),:);
        B = F(nnper(2),:);
        
        %% 交叉操作
        W = ceil(N/10);     % 交叉点个数
        p = unidrnd(N-W+1);   % 随机选择交叉范围，从p到p+W
        for i =1:W
            x = find(A==B(p+i-1));
            y = find(B==A(p+i-1));
            temp = A(p+i-1);
            A(p+i-1) =B(p+i-1);
            B(p+i-1) = temp;
            temp = A(x);
            A(x) = B(y);
            B(y) = temp;
        end
        
        %% 变异操作
        p1 = floor(1+N*rand());
        p2 = floor(1+N*rand());
        while p1==p2
            p1 = floor(1+N*rand());
            p2 = floor(1+N*rand());
        end
        tmp = A(p1);
        A(p1) = A(p2);
        A(p2) = tmp;
        tmp = B(p1);
        B(p1) = B(p2);
        B(p2) = tmp;
        F = [F;A;B];
        [aa,bb] = size(F);
    end
    if aa>NP
        F = F(1:NP,:);        % 保持种群规模为NP
    end
    f = F;                    % 更新种群
    f(1,:) = R;               % 保留每代最优个体
    clear F;
    gen = gen+1;
    Rlength(gen) = minlen;
end
 
%% 绘制图形
figure
for i = 1:N-1
    plot([C(R(i),1),C(R(i+1),1)],[C(R(i),2),C(R(i+1),2)],'bo-');
    hold on;
end
 
plot([C(R(N),1),C(R(1),1)],[C(R(N),2),C(R(1),2)],'ro-');
title(['优化最短距离：',num2str(minlen)]);
figure
plot(Rlength)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')