机器学习中的"距离"
@(神经网络)
在现代机器学习方法中,无论是有监督学习还是无监督学习都使用各种“度量”来得到不同样本数据的差异度或者不同样本数据的相似度。良好的“度量”可以显著提高算法的分类或预测的准确率。“度量”主要由两种,分别为距离、相似度和相关系数,距离的研究主体一般是线性空间中点;而相似度研究主体是线性空间中向量;相关系数研究主体主要是分布数据。下面我们对机器学习中的一些距离进行讨论。
L p L_p Lp距离
这个
L
p
L_p
Lp距离又称
L
p
L_p
Lp范数,只是在不同领域的叫法而已,范数是线性代数里面的一种称呼,向量的范数可以简单形象的理解为向量的长度,或者向量到零点的距离,或者相应的两个点之间的距离。p为不同常数的时候
L
p
L_p
Lp范数所适用的场景不同。
至于这里为什么讨论的是向量的范数呢,是因为计算机不能处理现实世界的文字、图像信息,我们需要将这些数据转化为张量才能被计算机处理。
向量的范数定义
向量的范数是一个函数 ∣ ∣ x ∣ ∣ ||x|| ∣∣x∣∣,满足非负性 ∣ ∣ x ∣ ∣ ≥ 0 ||x|| \geq 0 ∣∣x∣∣≥0,齐次性 ∣ ∣ c x ∣ ∣ = ∣ c ∣ ∣ ∣ x ∣ ∣ ||cx|| = |c| ||x|| ∣∣cx∣∣=∣c∣∣∣x∣∣ ,三角不等式 ∣ ∣ x + y ∣ ∣ < = ∣ ∣ x ∣ ∣ + ∣ ∣ y ∣ ∣ ||x+y|| <= ||x|| + ||y|| ∣∣x+y∣∣<=∣∣x∣∣+∣∣y∣∣。这里的$ || 是 以 后 经 常 会 遇 见 的 一 种 函 数 , 一 种 运 算 符 , 一 种 映 射 关 系 。 常 见 的 范 数 有 是以后经常会遇见的一种函数,一种运算符,一种映射关系。常见的范数有 是以后经常会遇见的一种函数,一种运算符,一种映射关系。常见的范数有L_0, L_1, L_2, L_\infty 等 , 统 一 记 为 等,统一记为 等,统一记为L_p$范数。
L 0 L_0 L0范数
L0范数: ∣ ∣ x ∣ ∣ 0 ||x||_0 ∣∣x∣∣0表示x向量各个非零元素的个数。 这里在引入一个概念,叫做汉明距离:
Hamming distance是指两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数。例如字符串“1111”与“1001”之间的汉明距离为2。
那么对于
∣
∣
x
∣
∣
||x||
∣∣x∣∣的
L
0
L_0
L0范数就可以看成是计算
∣
∣
x
∣
∣
||x||
∣∣x∣∣到
0
⃗
\vec0
0的汉明距离。
也就是如果我们使用
L
0
L_0
L0范数,即希望w的大部分元素都是0. (w是稀疏的)所以可以用于Machine Learning中做稀疏编码,特征选择。通过最小化
L
0
L_0
L0范数,来寻找最少最优的稀疏特征项。但不幸的是,
L
0
L_0
L0范数的最优化问题是一个NP hard问题,而且理论上有证明,
L
1
L_1
L1范数是
L
0
L_0
L0范数的最优凸近似,因此通常使用
L
1
L_1
L1范数来代替(看这个铺垫)。
L 1 L_1 L1范数
L1范数:
∣
∣
x
∣
∣
1
||x||_1
∣∣x∣∣1 为x向量各个元素绝对值之和。 如果说
L
0
L_0
L0范数可以看作是Hamming Distance,那么
L
1
L_1
L1范数被称作Manhattan Distance 就显得很正统了,想象你在曼哈顿要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直线距离吗?显然不是,除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源, 曼哈顿距离也称为城市街区距离(City Block distance)。 两个
n
n
n维向量
a
(
a
1
;
a
2
;
…
;
a
n
)
a(a1;a2;…;an)
a(a1;a2;…;an)与
b
(
b
1
;
b
2
;
…
;
b
n
)
b(b1;b2;…;bn)
b(b1;b2;…;bn)间的曼哈顿距离:
d
=
∑
k
=
1
n
∣
a
k
−
b
k
∣
d=\sum_{k=1}^n{|a_k-b_k|}
d=k=1∑n∣ak−bk∣
L
1
L_1
L1范数的解通常是稀疏性的,倾向于选择数目较少的一些非常大的值或者数目较多的insignificant的小值。按照和#
L
0
L_0
L0范数一样的理解的话就应该是
x
x
x到
0
⃗
\vec0
0的曼哈顿距离。
L 2 L_2 L2范数
L2范数:
∣
∣
x
∣
∣
2
||x||_2
∣∣x∣∣2为
x
x
x向量各个元素平方和的1/2次方,
L
2
L_2
L2范数又称Euclidean范数(欧氏距离)或者Frobenius范数。
L
2
L_2
L2范数应该是所有范数中最让我们熟悉的范数了,其实就是平面几何里的距离,其实我认为你完全可以吧p范数里的p理解为维度,
L
2
L_2
L2范数就是二维空间,
L
1
L_1
L1范数就是一维(
L
0
L_0
L0范数就比较尴尬了,这个仁者见仁吧)。
L
2
L_2
L2范数越小,可以使得w的每个元素都很小,接近于0,但与
L
1
L_1
L1范数不同的是他不会让它等于0而是接近于0.。由于
L
1
L_1
L1范数并没有平滑的函数表示,起初
L
1
L_1
L1最优化问题解决起来非常困难,但随着计算机技术的到来,利用很多凸优化算法使得
L
1
L_1
L1最优化成为可能。
L
2
L_2
L2范数的代数表示为:
d
=
(
a
−
b
)
T
(
a
−
b
)
2
d=\sqrt[2]{(a-b)^T(a-b)}
d=2(a−b)T(a−b)
L p L_p Lp范数
Lp范数:
∣
∣
x
∣
∣
p
||x||_p
∣∣x∣∣p为
x
x
x向量各个元素绝对值
p
p
p次方和的
1
/
p
1/p
1/p次方。这个时候他叫p范数,他也是Minkowski Distance(闵可夫斯基距离,简称闵氏距离),其代数表示为:
d
=
∑
k
=
1
n
∣
a
k
−
b
k
∣
p
p
d=\sqrt[p]{\sum_{k=1}^n{|a_k-b_k|}^p}
d=pk=1∑n∣ak−bk∣p
其中p是一个变参数。
当p=1时,就是曼哈顿距离
当p=2时,就是欧氏距离
当p→∞时,就是切比雪夫距离
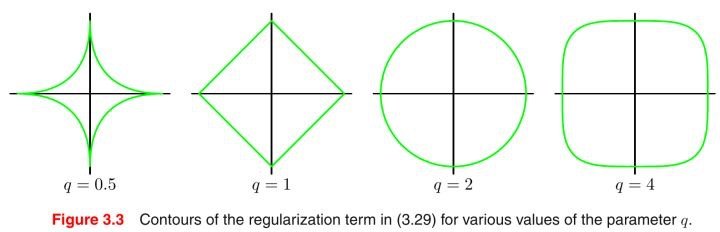
根据变参数的不同,闵氏距离可以表示一类的距离。用图形表示就是:
闵氏距离(包括曼哈顿距离、欧氏距离和切比雪夫距离。)都存在明显的缺点,如果用闵氏距离来度量相似度的时候,很可能出现度量衡不同的情况,放到实际场景中就是,先举个比较常用的例子,身高和体重,这两个变量拥有不同的单位标准,也就是有不同的scale。比如身高用毫米计算,而体重用千克计算,显然差10mm的身高与差10kg的体重是完全不同的。但在普通的欧氏距离中,这将会算作相同的差距。有意思…… 简单说来,闵氏距离的缺点主要有两个:
- 将各个分量的量纲(scale),也就是“单位”当作相同的看待了。
- 没有考虑各个分量的分布(期望,方差等)可能是不同的。
标准化欧式距离(Standardized Euclidean Distance)
那么如何针对一些特定的范数解决上面提到的这两个问题呢?最常讨论的就是Euclidean Distance的优化。既然在各个维度上的数据分布不同,那么我们将所有维度的数据都进行一次标准化,标准化到什么标准呢?那肯定是标准化到均值方差都相等啊,那么到底相等到多少呢?这里先复习点统计学知识吧,假设样本集X的均值(mean)为m,标准差(standard deviation)为s,那么X的“标准化变量”表示为:
X
′
=
X
−
m
s
X'=\frac{X-m}{s}
X′=sX−m。而且标准化变量的数学期望为0,方差为1。因此样本集的标准化过程(standardization)用公式描述就是:
x
∗
=
x
−
μ
δ
x^*=\frac{x-\mu}{\delta}
x∗=δx−μ。经过简单的推导就可以得到两个n维向量a(a1,a2,…,an)与 b(b1,b2,…,bn)间的标准化欧氏距离的公式:
d
=
∑
k
=
1
n
(
a
k
−
b
k
δ
k
)
2
p
d=\sqrt[p]{\sum_{k=1}^n{ (\frac{a_k-b_k}{\delta_k}) ^2 } }
d=pk=1∑n(δkak−bk)2
L ∞ L_\infty L∞范数
L
∞
L_∞
L∞范数:
∣
∣
x
∣
∣
∞
||x||_\infty
∣∣x∣∣∞为x向量各个元素绝对值最大那个元素的绝对值。这里又来一个名词叫做:切比雪夫距离 ( Chebyshev Distance ) 。国际象棋玩过么?(没玩过,因为我也是抄的别人的博客)国王走一步能够移动到相邻的8个方格中的任意一个。那么国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?自己走走试试。你会发现最少步数总是max( | x2-x1 | , | y2-y1 | ) 步 。有一种类似的一种距离度量方法叫切比雪夫距离:
d
=
max
k
∣
a
k
−
b
k
∣
o
r
d
=
lim
p
→
∞
(
∑
k
=
1
n
(
∣
a
k
−
b
k
∣
p
)
)
1
p
d=\max_k{|a_k-b_k|} or d = \lim_{p\rightarrow\infty}{(\sum_{k=1}^n(|a_k-b_k|^p))^\frac{1}{p}}
d=kmax∣ak−bk∣ord=p→∞lim(k=1∑n(∣ak−bk∣p))p1
事实上就是两个n维向量a(a1;a2;…;an)与 b(b1;b2;…;bn)间的曼哈顿距离。
##余弦距离(Cosine Distance)
几何中夹角余弦可用来衡量两个向量方向的差异,机器学习中借用这一概念来衡量样本向量之间的差异。在几何中余弦距离的计算公式如下:
c
o
s
(
θ
)
=
x
1
x
2
+
y
1
y
2
x
1
2
+
y
1
2
2
x
2
2
+
y
2
2
2
cos(\theta)=\frac{x_1x_2+y_1y_2}{\sqrt[2]{x_1^2+y_1^2}\sqrt[2]{x_2^2+y_2^2}}
cos(θ)=2x12+y122x22+y22x1x2+y1y2
这个思想进入线性代数后计算两个向量的夹角余弦就是:
c
o
s
(
θ
)
=
a
T
b
∣
a
∣
⋅
∣
b
∣
cos(\theta)=\frac{a^Tb}{|a|\cdot|b|}
cos(θ)=∣a∣⋅∣b∣aTb
夹角余弦取值范围为[-1,1]。夹角余弦越大表示两个向量的夹角越小,夹角余弦越小表示两向量的夹角越大。当两个向量的方向重合时夹角余弦取最大值1,当两个向量的方向完全相反夹角余弦取最小值-1。
##杰卡德系数(Jaccard coefficient)
杰卡德相似系数(Jaccard Similarit Coefficient)
两个集合A和B的交集元素在A,B的并集中所占的比例,称为两个集合的杰卡德相似系数,用符号J(A,B)表示。
J
(
A
,
B
)
=
∣
A
∩
B
∣
∣
A
∪
B
∣
J(A,B) = \frac{|A\cap B|}{|A\cup B|}
J(A,B)=∣A∪B∣∣A∩B∣
杰卡德相似系数是衡量两个集合的相似度一种指标。可将杰卡德相似系数用在衡量样本的相似度上。 样本A与样本B是两个n维向量,而且所有维度的取值都是0或1。
杰卡德距离(Jaccard Distance)
与杰卡德相似系数相反的概念是杰卡德距离(Jaccard distance)。杰卡德距离可用如下公式表示:
J
δ
(
A
,
B
)
=
1
−
J
(
A
,
B
)
=
∣
A
∪
B
∣
−
∣
A
∩
B
∣
∣
A
∪
B
∣
J_\delta(A,B) = 1 - J(A, B) = \frac{|A\cup B| - |A\cap B|}{|A\cup B|}
Jδ(A,B)=1−J(A,B)=∣A∪B∣∣A∪B∣−∣A∩B∣
杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。
相关性
和上面杰卡德系数一样,相关性也存在两个度量衡。
相关系数 ( Correlation coefficient )
相关系数的定义:
ρ
X
Y
=
c
o
n
v
(
X
,
Y
)
d
(
X
)
d
(
Y
)
=
E
(
(
X
−
E
X
)
(
Y
−
E
Y
)
)
d
(
X
)
d
(
Y
)
\rho_{XY} = \frac{conv(X, Y)}{\sqrt{d(X)}\sqrt{d(Y)}} = \frac{E((X-EX)(Y-EY))}{\sqrt{d(X)}\sqrt{d(Y)}}
ρXY=d(X)d(Y)conv(X,Y)=d(X)d(Y)E((X−EX)(Y−EY))
相关系数是衡量随机变量X与Y相关程度的一种方法,相关系数的取值范围是[-1,1]。
相关系数的绝对值越大,则表明X与Y相关度越高。
当X与Y线性相关时,相关系数取值为1(正线性相关)或-1(负线性相关)。
相关距离(Correlation distance)
相关距离的定义:
D
X
Y
=
1
−
ρ
X
Y
D_{XY} = 1- \rho_{XY}
DXY=1−ρXY
马氏距离(Mahalanobis Distance)
马氏距离是一种距离的度量,可以看作是欧氏距离的一种修正,修正了欧式距离中各个维度尺度不一致且相关的问题。对于单个数据点的马氏距离:
D
M
(
x
)
=
(
x
−
μ
)
T
(
∑
(
x
−
μ
)
)
−
1
D_M(x) = \sqrt{(x-\mu)^T(\sum(x-\mu))^{-1}}
DM(x)=(x−μ)T(∑(x−μ))−1
数据点x, y之间的马氏距离:
D
M
(
x
)
=
(
x
−
y
)
T
(
∑
(
x
−
y
)
)
−
1
D_M(x) = \sqrt{(x-y)^T(\sum(x-y))^{-1}}
DM(x)=(x−y)T(∑(x−y))−1
其中
Σ
Σ
Σ是多维随机变量的协方差矩阵,
μ
μ
μ为样本均值,如果协方差矩阵是单位向量,也就是各维度独立同分布,马氏距离就变成了欧氏距离。
信息熵(Information Entropy)
信息熵并不属于一种相似性度量,但是在整个Machine Learning的学习中可以说是很重要了,而且和这个信息度量也算是有点关联,所以写在这里。信息熵是衡量分布的混乱程度或分散程度的一种度量。分布越分散(或者说分布越平均),信息熵就越大。分布越有序(或者说分布越集中),信息熵就越小。计算给定的样本集X的信息熵的公式:
e
n
t
r
o
p
y
=
−
∑
i
=
1
C
p
i
l
o
g
2
(
p
i
)
entropy=-\sum_{i=1}^C{p_ilog_2(p_i)}
entropy=−i=1∑Cpilog2(pi)
其中
C
C
C表示样本集X的分类数,
p
i
p_i
pi表示
X
X
X中第
i
i
i类元素出现的概率。信息熵越大表明样本集
S
S
S分类越分散,信息熵越小则表明样本集
X
X
X分类越集中。当
S
S
S中
C
C
C个分类出现的概率一样大时(都是
1
C
\frac{1}{C}
C1),信息熵取最大值
l
o
g
2
C
log_2C
log2C。当
X
X
X只有一个分类时,信息熵取最小值0。
不要脸环节
如果你觉得我的文章写的还可以,我不介意你给我点赞呢,赞助支持也可以鸭。如果有什么地方有误欢迎评论区指正谢谢。

硬核引流:欢迎大家推广关注我的公众号啊(洋可喵)!!!

参考链接
fanrupin——L0/L1/L2/Lp/L∞范数的联系与区别
知乎——0 范数、1 范数、2 范数有什么区别?
Yan文怡——关于数据建模变量标准化,你想知道的都在这里了





















 3102
3102

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








