关于kNN的一切

关于kNN的一切

@(神经网络)

kNN定义

在模式识别领域中，最近邻居法（KNN算法，又译K-近邻算法，K Nearest-Neighbor ）是一种用于分类和回归的非参数统计方法[1]。在这两种情况下，输入包含特征空间（Feature Space）中的k个最接近的训练样本。

——Wikipedia “ K-近邻算法”

别人的话总是那么高大上晦涩难懂，说得简单一点，kNN就是一个巨几把简单的一个算法，算是机器学习算法里面最简单的一个了吧，首先我们要明确这是一个**分类算法**，而且这是一个有监督的分类算法。和神经网络不同，我感觉这个算法实际上是不需要训练的，但是有的还在划分训练集和测试集，搞不懂，个人觉得网上那些划分训练集是为了查看模型的情况，但是我又认为如果没有参数需要训练的话，应该也不叫做训练集吧emmmmm，纯属个人胡诌，具体请教各位看官了。

kNN思想

为什么要单独列一段呢，是因为单独列一段好看吗？是的哈哈哈。kNN的思想很简单，假设我们有一个样本空间（俗称数据集），在该样本空间的任一样本点的类别我们由它周围最近的k个邻居来就决定，每个邻居的类别表示一票，票数最多的那个类别就是我们预测的类别。

但是基于这样的思想，我们在实际操作的过程中，想要得到最近的几个邻居的话就必须要加载所有的数据，并将该样本点对特征空间中的所有其他样本进行两两计算，可以想见，当样本空间足够大的时候，进行一次计算需要的时空复杂度，那么如何解决这个问题呢，后面会讲。

第二，假设我们要做implementation的话，如何去度量两个样本点的距离呢？这里请参考我前面的文章（顺便做个推广）——机器学习中的”距离”，由于样本点的特征可能不止一个维度，所以一半样本点都是高维向量，可以采用Euclidean Distance、Manhattan Distance等等都是OK的。

这个k我们已经通过定义可以知道，k代表需要找到的最近的几个邻居，那么具体应该设为几个呢，这个主要就是看你自己的算法了，理论上讲，在一定的数据区间内，k值越大对于当前样本空间的拟合程度越高，但是实际模型的泛化能力就越弱，所以具体这里k的选取还需要根据实际的运用场景来定。

Implementation of kNN

像这种十大机器学习经典算法个人还是觉得有实现一下的必要的，从python底层实现一下，虽然像tensorflow，numpy，scipy这些框架都已经有封装好的库了，但是知道原理总是好的，而且有利于优化啊。

这里的数据集采用的是网上海伦对于自己的约会对象的数据，数据可以点此下载，其中ins.txt是数据集的说明，真实的数据集是``，文件一共有四列，每一行为一个约会对象的信息（“每年获得的飞行常客里程数”，“玩视频游戏所消耗的时间百分比”，“每周消费的冰激凌公斤数”），最后一列是海伦对他的评价（1-不喜欢的人，2-魅力一般的人，3-极具魅力的人）。 数据一共有1000列，不要问我为什么她约会了那么多人还搜集的是这些数据，因为我也不知道。

数据集的处理的话我们选用了pandas和numpy，我的处理方式是首先把它转化成一个csv，方便pandas处理，因为习惯，这个看个人吧，处理的代码如下：

with open("data/datingTestSet2.txt", "r", encoding="utf-8") as fopen:
    with open("data/data.csv", "w", encoding="utf-8") as fwrite:
        content = fopen.readlines()
        for line in content:
            data = line.replace("	", ",")
            fwrite.write(data)

然后读入数据：

import pandas as pd
import numpy as np
from scipy import stats

#读入数据
data = pd.read_csv("data/data.csv", header=None)
data['4'] = range(len(data))

然后定义计算距离的函数，numpy底层是定义了计算Minkowski Distance的函数np.linalg.norm()，你也可以自己实现。

def distance(vec_one, vec_two, r):
    return np.linalg.norm(vec_one - vec_two, r)

你需要一个函数计算最近的k个邻居，同时获得最高投票数的那个标签作为预测值：

def neighbour(trainSet, testInstance, r, k):
    dis = []
    for index,ts in trainSet.iterrows():
        dis.append([distance(ts[:2], testInstance[:2], r), ts['4']])
    dis.sort(key=lambda x:x[0])
    neighs = []
    for i in range(1, k+1):
        lineNum = int(dis[i][1])
        neighs.append(trainSet.loc[lineNum])
    return neighs

def get_predict_result(neighbors):
    most = [n[3] for n in neighbors]
    return stats.mode(most)[0][0]

然后就和网上一样我也要划分一个测试集和训练集（真香，大家都划分我也划分，从众心理作祟了哈哈哈），以8:2划分`，然后待入计算。

trainset_len = (int)(0.8 * len(data))

trainSet = data[:trainset_len]
testSet = data[trainset_len:]
for index,ts in trainSet.iterrows():
    nei = neighbour(trainSet, ts, np.infty, 3)
    print('>predict label is: ', get_predict_result(nei), 'and real label is: ', ts[3])

然后针对测试集我们应该查看其准确率，定义一个计算准确率的函数，然后调用：

def get_acc(testSet, r, k):
    count = 0
    for index,ts in testSet.iterrows():
        print("progress:", index/len(testSet))
        nei = neighbour(testSet, ts, r, k)
        if(get_predict_result(nei) == ts[3]):
            count += 1
    return count / len(testSet)

acc = get_acc(testSet, np.infty, 4)
print("Accuracy is: ", acc)

运行效果如下：

大功告成，其实正常情况下你应该再做一次Visualization，对于二维特征的Visualization很好做，直接在一个二维坐标系里就可以完成，我们现在的是三维的话就比较麻烦了，由于我是个比较水的人，就不做可视化了，别人做出来的可视化大概长这个亚子（这个别人就是Stanford University哈哈哈哈，突然觉得自己很鸡贼）：

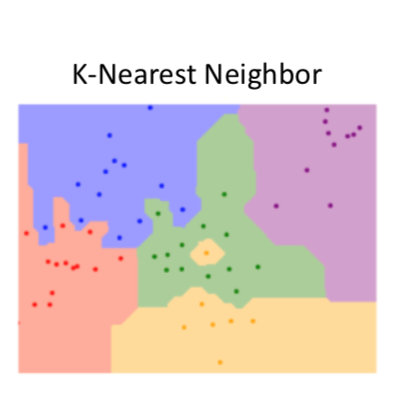
你也可以调节计算距离和邻居的个数，也就是上面代码中k和r的值，我调节了几次的结果如下：

2 3 0.825
2 4 0.815
1 3 0.825
1 4 0.815
infty 3 0.825
infty 4 0.825

发现距离的选择貌似对这组数据的影响并不大，然而邻居个数的影响倒是有0.01，有意思哈哈哈。准确率82.5%。

总结

在KNN中，主要有以下两点优势：

1. 通过计算对象间距离来作为各个对象之间的非相似性指标，避免了对象之间的匹配问题，在这里距离一般使用欧氏距离或曼哈顿距离；
2. 同时，KNN通过依据k个对象中占优的类别进行决策，而不是单一的对象类别决策。

缺点也很明显，我上面提了，可以优化比如建树索引等等，后面有时间来整整。

不要脸环节

如果你觉得我的文章写的还可以，我不介意你给我点赞呢，赞助支持也可以鸭。如果有什么地方有误欢迎评论区指正谢谢。

硬核引流：欢迎大家推广关注我的公众号啊（洋可喵）！！！