函数种类-匿名\高阶\递归

普通函数

        参数作用：函数外部向函数内部传递数据的一个通道

        形参：定义函数时定义

        实参：调用函数时传递的参数

        --------------------------------------------------------后期再补充

匿名函数：很少单独使用，基本上跟高阶函数一起使用

       使用场景：

         1.函数体非常简单

         2.使用次数较少

      作用：简化函数，适用短小函数

      格式：lambda 参数:返回值

     注意点： s=lambda a,b :a+b ，此时s是函数名地址，所以需要调用res=s(1,2)才能运行lambda里面的代码。res才是代码运行之后的结果。

使用场景：
# 根据数字大小进行排序
li1=[("a",1),("b",21),("c",6)]

print(sorted(li1, key=lambda x: x[1]))


返回结果：
[('a', 1), ('c', 6), ('b', 21)]

高阶函数：把函数作为参数进行传递的函数

        sorted(iterable,key,reverse)：sorted方法可以对所有可迭代对象进行排序

                参数： 第一个参数：可迭代对象，第二个key=排序指定规则，reverse=默认False 正序排列，True倒序排列

排序字典：
stu={"果果":7,"liuliu":12,"yiyi":3}
print(dict(sorted(stu.items(),key=lambda x:x[1])))

输出结果：
{'yiyi': 3, '果果': 7, 'liuliu': 12}

         map()：映射

                将可迭代对象，放入函数中，根据函数内部进行处理，并返回结果，放到一个新的对象中。

print(map(lambda x,y:{x:y},["果果","liuliu","yiyi"],[5,3,6]))


输出结果：
<map object at 0x000001E13F96A2B0>


可将结果转为列表：
print(list(map(lambda x,y:{x:y},["果果","liuliu","yiyi"],[5,3,6])))

或者是用列表推导式：
new=map(lambda x,y:{x:y},["果果","liuliu","yiyi"],[5,3,6])
print([ i for i in new])

输出结果：
[{'果果': 5}, {'liuliu': 3}, {'yiyi': 6}]

        fitler(函数,iterable) :过滤器，返回是一个对象

                第一个参数为None，那么返回都是真的数据

学习视频：千锋Python教程：86-高阶函数(filter,reduce)_哔哩哔哩_bilibili

num=filter(lambda x:x<10,[11.77,5,89,78,22,1,2,5,6,3,55,1,8.5])
print([i for i in num])


输出结果：
[5, 1, 2, 5, 6, 3, 1, 8.5]

        reduce(function,sequence)   ：

                使用场景：对列表中的元素进行加减乘除运算的函数

                function：函数的参数必须是两个

from functools import reduce

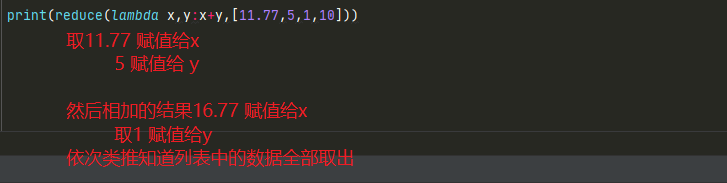
print(reduce(lambda x,y:x+y,[11.77,5,1,10]))



返回结果：
27.77

解析图：

        偏函数：

        partial（）将一个函数的部分参数预先绑定为某些值，从而得到一个新的具有较少可变参数的函数。

from functools import partial
#使用场景，比如我需要固定一个值与其他值进行相加
def add(x,y):
    return x+y




change=partial(add,3)  # 需求中并不在意这个3绑定在哪一个参数上
print(change(7))
print(change(8))
print(change(10))
 


返回结果：
10
11
13

        warps（）:使用装饰器后，消除装饰器带来的副作用

递归函数: 在函数的定于中,调用函数自身,递归函数

        注意点:必须要有一个出口点,不然会报超出递归深度的错误

学习网址:千锋Python教程：99 递归函数_哔哩哔哩_bilibili

def g(n):
    """该函数用于求任意数的阶层,
    参数:n要求阶层的数字
    """
    # 基线条件,给出结束递归的条件
    if n == 1:
        return 1
    
    # 你想要函数做什么操作,是需要什么样的算法
    return g(n-1) + n


print(g(5))



输出结果为:
15

递归解析图:

面试题:斐波那契数列  知识点来源-千峰

1. 使用循环的方式解决
def fuc(n):
    res=[]
    for i in range(n):
        if i ==0 or  i == 1:
            res.append( 1)
        else:
            res.append(res[i-1] + res[i-2])
    return res


print(fuc(10))


输出结果:
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]

解析思路:

方式2:使用递归

def fun(n):
    if n == 1 or n == 2:  #那么这边修改第一个第二个值为1和2
        return 1
    return fun(n-1)+fun(n-2)


print([fun(i) for i in range(1,7)]) # 列表推导式输出
# 因为range默认是从0开始的，如果是按我们常规的第一个第二个，那么就需要指定从1开始




输出结果:

8
[1, 1, 2, 3, 5, 8]

解析图:

函数内部开始值做了修改，但是运行原理是一样的