回溯法笔记与个人体会

回溯法

定义：

回溯法是一种选优搜索法，即探索与回溯法，又称为试探法，安选优条件向前搜索，以达到目标。如果探索到某一步时，发现无法达到最优解或者无解，则退回到上一步，即回溯，直到选出最优解为止。

//通俗来说这个更加像人的思考方式，虽然有点笨，但是有一定的取舍，能够做出一定的简单的解值和边界判断。

1. 回溯法的框架：
2. 问题的解空间
3. 回溯法的基本思想
4. 递归回溯
5. 迭代回溯
6. 子集树和排列树

 

回溯点：

满足回溯条件的某个状态点称为回溯点。

//即在回溯过程中之前走到的位置，可以是上个选择，也可以是根据算法自定条件的位置，甚至可以是原点，但是一般不考虑原点，会出现死循环。当然也可以采取一定的方法避免。

解空间

在回溯算法中，每次需要扩大当前部分解时，都会面临一个未选集中的可选集合，新的部分解就在该集合中构造而成。这样的集合装态，其结构是一棵二叉树，树根是初始状态，每个叶子节点代表一个解，一个子节点代表当前部分的一个可能解。每个节点的子节点就是在它的基础上扩展而成的下一部分解。这样的装态集合称为状态空间集合树。

//回溯思想就是将可供选择的解都搜索一遍，与穷举法的思路基本一致，从实现看，穷举法构成的树必定有2^n-1个节点，有2^(n-1)个解，但是回溯法会采取剪枝和边界判断，所以生成的树会少于穷举法，当然不恰当的剪枝和边界判断同样会导致算法效率降低。

回溯法的基本思想：

回溯法对任一解的生成，一般都采用逐步扩大部分解的方式。每前进一步，都试图在当前部分解的基础上扩大该部分解。它在问题的装态空间树中，从开始结点（根节点）除法，以深度优先搜索整个装态空间。这个开始结点就成为了一个活结点，同时也成为了当前的扩展结点。在当前的扩展结点出，搜索向纵深方向移至一个新结点。这个节点成为新的活结点，并成为当前扩展结点。如果在当前扩展结点出不能再向纵深方向移动，则当前扩展结点就成为死结点。此时，应当往回移动（回溯）至最近的活结点处，并使这个结点成为扩展结点。回溯法以这种工作方式递归地在状态空间中搜索，直到找到所要求的解或解空间中已无活结点时为止。

//个人理解：一个节点只要再其子节点未完成搜索之前都是活结点，但是只有当前结点是扩展结点。

如图。

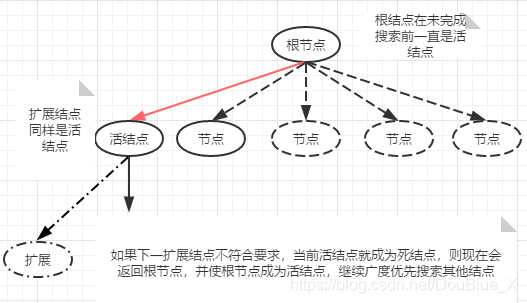
回溯法与穷举法有某些联系，它们都是基于试探的。穷举法要将一个解的各个部分全部生成后，才检查是否满足条件，若不满足，则直接放弃该完整解，然后再尝试另一个可能的完整解，它并没有沿着一个可能的完整解的各个部分逐步回退生成解的过程。而对于回溯法，一个解的各个部分是逐步生成的，当发现当前生成的某部分不满足约束条件时，就放弃该步所做的工作，退到上一步进行新的尝试，而不是放弃整个解重来。

//即看过程还是看结果，回溯法像是人在面对问题时一步一步向前走，注重在过程，而穷举法则更像是眉毛胡子一把抓，不管对错，先求一个结果集合，再从集合中找最优，而回溯注重过程，在得到一个最优解后就可以放弃其他明显不是最优解的部分求解，虽然回溯法中有很大的穷举法的影子，但是面对不同的需求各有各的长处。

两种回溯方法

递归回溯

回溯法对解空间的深度优先系统，一般可用以下递归函数实现

void backtrack（int t）{//t表示递归深度

if (t > n) output(x);//到达叶节点时，由此记录或者输出。

else {

for(int i=f(n,t);i<g(n,t);i++){//遍历搜索当前结点的子结点

x[t]=h(i);//h(i)表示当前扩展结点的可选值

if(constrain(t)&&Bound(t))backtrack(t+1);//如果满足约束和边界条件进行下一层递归。约束条件和边界条件是完成剪枝的主要部位。

}

}

}

迭代回溯

如果不使用递归回溯进行深度遍历，可以将回溯法表示为以下过程：

void IterativeBacktrack(void ){

int t=1;

while(t>0){

if(f(n,t)<=g(n,t)){

for(int i=f(n,t);i<g(n,t);i++){

x[t]=h(i);

if(Constraint(t)&&Bound(t)){

if(Solution(t)){//判断是否存在可行解

output(x);

}

else

t++;

}

}

}

}

}

子集树与排列树

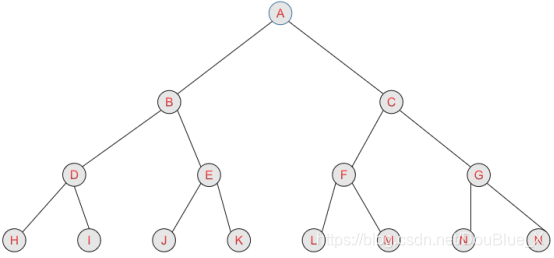
子集树

   当所给问题是确定 n个元素的集合S中找出满足某种性质的子集时，相应的解空间树称为子集树。

对子集树的搜索

void backtrack（int t）{//t表示递归深度

if (t > n) output(x);

else {

for(int i=f(n,t);i<g(n,t);i++){

x[t]=h(i);

if(constrain(t)&&Bound(t))backtrack(t+1);。

}

}

}

 

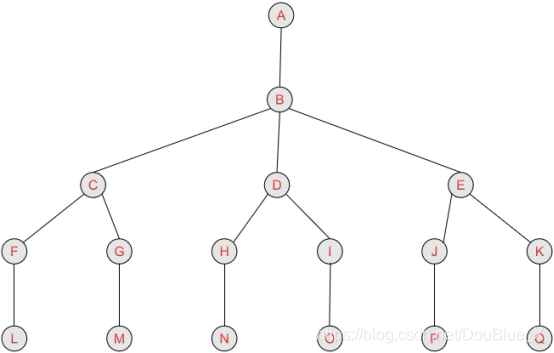
排列树

   当所给问题是确定n各元素的满足某种性质的排列时，相应的解空间树称为排列树。

对排列树的搜索

void Backtrack(int t){

if(t>n)

output(x);

else {

for(int i=;i<=n;i++){

Swap(x[t],x[i]);

if(Constraint(t)&&Bound(t))Backtrack(t+1);

Swap(x[t],x[i]);

}

}

}

回溯法的复杂度

回溯算法解题的一个显著特征，是在搜索解的过程中动态的产生问题的解空间。在任何时候，算法只保存从根节点到当前扩展结点的路劲。如果解空间树中从根节点到叶节点的最长路径的长度为h(n),则回溯法所需要的计算空间通常为O(h(n))。显式的存储存储整个解空间则需要O(2^h(n))或者O(h(n)!)内存空间。

而对应的时间复杂度则需要根据不同的算法进行分析。

参考 王晓东 著作 教材 《计算机算法分析与设计 》第五版