目录
树
树是一种非线性的数据结构
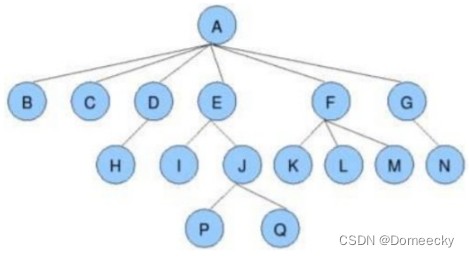
术语
节点的度:一个节点含有的子树个数
树的度:一棵树中节点的最大度数
叶节点:无分支节点的节点(度为 0 的节点)
父节点:连接该节点的上一层节点
子节点:该节点连接的下一层节点
兄弟节点:具有相同父节点,或父节点都在同一层的节点
节点的层次:根节点为第一层,往下依次 +1
树的高度:树中节点最大层次
树的表示
使用两个指针,分别指向其第一个子节点与右边第一个兄弟节点,即可遍历数组
typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _pNextBrother; // 指向其下一个兄弟结点
DataType _data; // 存放的数据
};
二叉树
每个节点最多有 2 个子节点的树
特殊二叉树
特殊二叉树分为「满二叉树」和「完全二叉树」。
满二叉树
若二叉树的每个节点都有两个子节点,节点数量为 2^h - 1(h 为树的高度),这棵树为满二叉树。
完全二叉树
由满二叉树演变而来,其高度与满二叉树相同,最后一层剩余的节点顺序与满二叉树对应
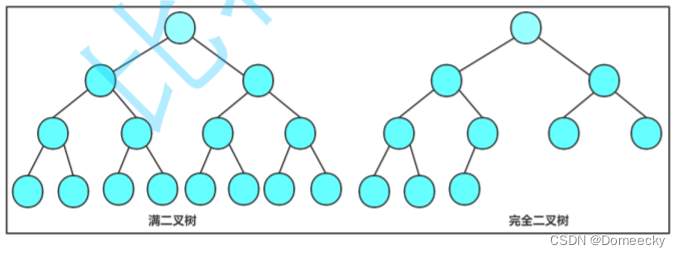
二叉树的存储结构
二叉树的存储结构分为「顺序存储」和「链式存储」
顺序存储
(1)使用数组存储,只适合用来表示完全二叉树,否则会有空间浪费。
(2)顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
(3)只有堆才会使用顺序存储。
链式存储
用链表来表示一棵二叉树,使用两个指针分别指向自己的左右子节点。
堆
堆分为「大堆」和「小堆」
小堆:所有节点的子节点都大于父节点
大堆:所有节点的子节点都小于父节点
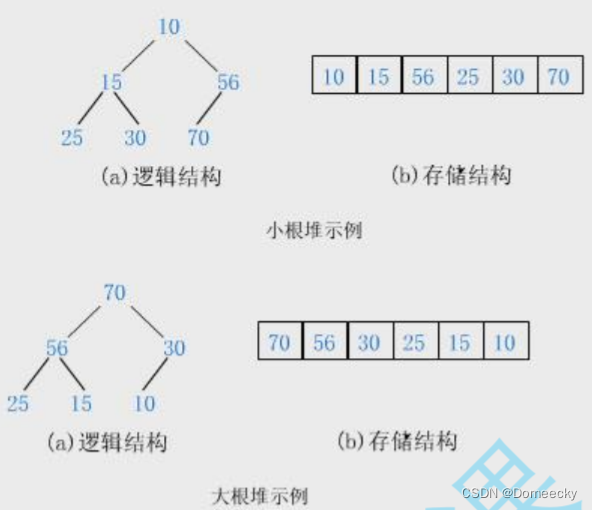
堆的结构特点
父节点 = (子节点 - 1)/ 2
左子节点 = 父节点 * 2 + 1
右子节点 = 父节点 * 2 + 2
堆的实现(小堆)
头文件
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
typedef int HPDataType;
typedef struct Heap
{
HPDataType* data;//存储数据的数据
int cap;//当前堆的容量
int size;//当前堆中的元素数量
}HP;
void HeapInit(HP* php);//初始化堆
void HeapDestroy(HP* php);//释放堆
void HeapPush(HP* php, HPDataType x);//插入数据并调整位置
void HeapPop(HP* php);//删除堆顶元素并调整位置
HPDataType HeapTop(HP* php);//返回堆顶元素
bool HeapEmpty(HP* php);//判断堆是否为空
int HeapSize(HP* php);//返回堆内当前元素个数源文件
#include"Heap.h"
void HeapInit(HP* php)//初始化堆
{
assert(php);
php->cap = php->size = 0;
php->data = NULL;
}
void HeapDestroy(HP* php)//释放堆
{
assert(php);
free(php->data);
php->cap = php->size = 0;
}
void Swap(HPDataType* a, HPDataType* b)//交换元素
{
HPDataType tmp = *a;
*a = *b;
*b = tmp;
}
void AdJustUp(HPDataType* data, int child)//向上调整位置
{
assert(data);
//父节点位置
int parent = (child - 1) / 2;
while (child > 0)
{
//若数据小于父节点则交换位置
if (data[child] < data[parent])
Swap(&data[child], &data[parent]);
//迭代
child = parent;
parent = (child - 1) / 2;
}
}
void HeapPush(HP* php, HPDataType x)//插入数据并调整位置
{
assert(php);
//检查是否需要扩容
if (php->cap == php->size)
{
int newcap = php->cap == 0 ? 4 : (2 * php->cap);
HPDataType* obj = (HPDataType*)realloc(php->data, sizeof(HPDataType) * newcap);
assert(obj);
php->data = obj;
php->cap = newcap;
}
//插入数据
php->data[php->size] = x;
php->size++;
//从下往上上调整位置
AdJustUp(php->data, php->size - 1);
}
void AdJustDown(HPDataType* data, int size, int parent)
{
assert(data);
//假设左子节点为最小子节点
int minchild = parent * 2 + 1;
while (minchild < size)
{
//比较左子节点和右子节点哪个更小
if (minchild + 1 < size && data[minchild] > data[minchild + 1])
minchild++;
//若子节点小于父节点则交换位置
if (data[parent] > data[minchild])
Swap(&data[parent], &data[minchild]);
//迭代
parent = minchild;
minchild = parent * 2 + 1;
}
}
void HeapPop(HP* php)//删除堆顶元素并调整位置
{
assert(php);
if (HeapEmpty(php))
return;
//将堆顶元素和堆底元素交换,再删除堆底元素
Swap(&php->data[0], &php->data[php->size - 1]);
php->size--;
//从上往下调整位置
AdJustDown(php->data, php->size, 0);
}
HPDataType HeapTop(HP* php)//返回堆顶元素
{
assert(php);
assert(!HeapEmpty(php));
return php->data[0];
}
bool HeapEmpty(HP* php)//判断堆是否为空
{
assert(php);
return php->size == 0;
}
int HeapSize(HP* php)//返回堆内当前元素个数
{
assert(php);
return php->size;
}堆排序
使用堆将数组进行排序
思路:堆排序分为两大步:「建堆」和「排序」。先将数组进行建堆,升序建大堆,降序建小堆,由于堆顶始终为最大或最小值,只需将最顶元素与堆底元素互换,这时堆底就为最值,又因为其他元素位置没变,所以只需将堆顶元素进行调整,无视堆底元素,再次互换,以此类推。
建堆
建堆使用 AdJustUp「上排序建堆」和AdJustDown「下排序建堆」皆可
上排序建堆
时间复杂度:O(N * logN)
从第二个节点开始,与父节点比较,依次向后遍历数组。
int main()
{
int arr[5] = { 5, 4, 3, 2, 1 };
int size = sizeof(arr) / sizeof(int);//数组长度
for (int i = 1; i < size; i++)
{
AdJustUp(arr, i);//依次向后遍历调整
}
return 0;
}下排序建堆
时间复杂度:O(N)
从最后一个非叶节点开始,与子节点比较,依次向上遍历数组。
最后一个非叶节点 = 最后一个节点的父节点 = (元素个数 - 1 - 1)/ 2
注:元素个数 - 1 得到最后一个节点,(最后一个节点 - 1)/ 2 得到父节点
int main()
{
int arr[5] = { 5, 4, 3, 2, 1 };
int size = sizeof(arr) / sizeof(int);//数组长度
for (int i = (size - 1 - 1) / 2; i >= 0; i--)
{
AdJustDown(arr, size, i);//依次向前遍历调整
}
return 0;
}
排序
void HeapSort(int* arr, int size)
{
for (int i = size - 1; i > 0; i--)// i 为最后一个元素
{
//交换堆顶元素和堆底元素
Swap(&arr[0], &arr[i]);
//将堆顶元素向下调整
AdJustDown(arr, i, 0);
}
}Top-K 问题
求前 K 个最大或最小元素
思路:求最大值使用小堆,求最小值使用大堆。先将整个数据中前 K 个元素依次放入堆中并调整,将剩余元素依次与堆顶元素比较大小并调整位置。
int main()
{
int arr[9] = { 1, 100, 3, 3, 3, 4, 1, 200, 300 };
int size = sizeof(arr) / sizeof(int);
int k = 3;
int heap[3] = { 0 };//创建堆
for (int i = 0; i < k; i++)
{
//将原数据的前 k 个进行拷贝
heap[i] = arr[i];
}
for (int i = 1; i < k; i++)
{
//对拷贝进来的元素进行建堆
AdJustUp(arr, i);
}
for (int i = k; i < size; i++)
{
//依次比较原数据剩下的元素并调整位置
if (heap[0] < arr[i])
{
heap[0] = arr[i];
AdJustDown(heap, k, 0);
}
}
return 0;
}链式结构实现
头文件
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType val;
struct BinaryTreeNode* left;//指向左子节点
struct BinaryTreeNode* right;//指向右子节点
}BTNode;
void PreOrder(BTNode* root);//前序遍历:根 → 左子树 → 右子树
void InOrder(BTNode* root);//中序遍历:左子树 → 根 → 右子树
void PostOrder(BTNode* root);//后序遍历:左子树 → 右子树 → 根
int TreeSize(BTNode* root);//返回树中节点个数
int TreeLeafSize(BTNode* root);//返回树中叶节点个数
int TreeHeight(BTNode* root);//返回树的高度
int TreeKLevel(BTNode* root, int k);//返回第 K 层的节点数量
BTNode* TreeFind(BTNode* root, BTDataType x);//寻找 x 并返回该节点
void TreeDestroy(BTNode* root);//释放二叉树源文件
#include"BinaryTree.h"
void PreOrder(BTNode* root)
{
if (root == NULL)
return;
printf("%d ", root->val);
PreOrder(root->left);
PreOrder(root->right);
}
void InOrder(BTNode* root)
{
if (root == NULL)
return;
InOrder(root->left);
printf("%d ", root->val);
InOrder(root->right);
}
void PostOrder(BTNode* root)
{
if (root == NULL)
return;
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->val);
}
int TreeSize(BTNode* root)
{
//返回左子树总结点 + 右子树总结点 + 自身
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
//判断该节点是否为叶节点
if (root->left == NULL && root->right == NULL)
return 1;
//返回左叶节点和右叶节点总和
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
int TreeHeight(BTNode* root)
{
if (root == NULL)
return 0;
//分别求出左子树和右子树的高度
int LeftTree = TreeHeight(root->left);
int RightTree = TreeHeight(root->right);
//返回较高的子树加上自己的高度
return LeftTree > RightTree ? LeftTree + 1 : RightTree + 1;
}
int TreeKLevel(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
return 0;
// k == 1 时正好在第 k 层
if (k == 1)
return 1;
//继续向下
return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right , k - 1);
}
BTNode* TreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->val == x)
return root;
//从左子树中找
BTNode* lret = TreeFind(root->left, x);
//若找到了直接返回
if (lret)
return lret;
//从右子树中找
BTNode* rret = TreeFind(root->right, x);
if (rret)
return rret;
//左右子树都没找到返回空
return NULL;
}
void TreeDestroy(BTNode* root)
{
if (root == NULL)
return;
//使用后序遍历释放二叉树的各个节点
TreeDestroy(root->left);
TreeDestroy(root->right);
free(root);
root = NULL;
}链式二叉树相关练习
(1)965. 单值二叉树 - 力扣(LeetCode) https://leetcode.cn/problems/univalued-binary-tree/
思路:递归比较父节点与子节点,若有一个值不相等则返回假,到达空节点则返回真
bool isUnivalTree(struct TreeNode* root){
if (root == NULL)
return true;
if (root->left && root->val != root->left->val)
return false;
if (root->right && root->val != root->right->val)
return false;
return isUnivalTree(root->left) && isUnivalTree(root->right);
}(2)100. 相同的树 - 力扣(LeetCode) https://leetcode.cn/problems/same-tree/
思路:依次比较两个树的相同位置,若同位置节点的值不同则返回假,当两棵树的节点都为空时则返回真
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if (p == NULL && q == NULL)
return true;
if ((p == NULL && q != NULL) || (p != NULL && q == NULL))
return false;
if (p->val != q->val)
return false;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}(3)144. 二叉树的前序遍历 - 力扣(LeetCode) https://leetcode.cn/problems/binary-tree-preorder-traversal/
思路:先计算出节点个数,开辟出对应空间,再将前序遍历中得到的数据依次放入数组。
int TreeSize(struct TreeNode* root)
{
if (root == NULL)
return 0;
return 1 + TreeSize(root->left) + TreeSize(root->right);
}
void PreOrder(struct TreeNode* root, int* arr, int* pi)
{
if (root == NULL)
return;
arr[(*pi)++] = root->val;
PreOrder(root->left, arr, pi);
PreOrder(root->right, arr, pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
int size = TreeSize(root);//计算节点个数
int* arr = (int*)malloc(sizeof(int) * size);//开辟对应大小空间
int i = 0;//指向数组的下标
PreOrder(root, arr, &i);//将节点中数据放入数组
*returnSize = size;//修改为数组对应大小
return arr;
}(4)572. 另一棵树的子树 - 力扣(LeetCode) https://leetcode.cn/problems/subtree-of-another-tree/
思路:写一个判断两棵树是否相等的函数,遍历 root,使用该函数与 subRoot 做比较。
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if (p == NULL && q == NULL)
return true;
if ((p == NULL && q != NULL) || (p != NULL && q == NULL))
return false;
if (p->val != q->val)
return false;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
if (root == NULL)
return false;
if (isSameTree(root, subRoot) == true)
return true;
return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}(5)二叉树遍历_牛客题霸_牛客网 https://www.nowcoder.com/practice/4b91205483694f449f94c179883c1fef?tpId=60&&tqId=29483&rp=1&ru=/activity/oj&qru=/ta/tsing-kaoyan/question-ranking
思路:先使用前序创建树,再使用中序打印树。
typedef char BTDataType;
typedef struct BinaryTreeNode {
BTDataType val;
struct BinaryTreeNode* left;//指向左子节点
struct BinaryTreeNode* right;//指向右子节点
} BTNode;
//使用前序创建树
BTNode* CreateTree(char* str, int* pi)
{
if (str[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
root->val = str[*pi];
(*pi)++;
root->left = CreateTree(str, pi);
root->right = CreateTree(str, pi);
return root;
}
//中序打印
void InOrder(BTNode* root)
{
if (root == NULL)
return;
InOrder(root->left);
printf("%c ", root->val);
InOrder(root->right);
}
int main() {
char str[100] = "0";
scanf("%s", str);
int i = 0;
BTNode* root = CreateTree(str, &i);
InOrder(root);
return 0;
}(6)层序遍历
思路:使用队列,放入树的第一个节点,再 Pop,Pop 后将该节点不为空的左子节点与由子节点依次 Push 进队列,以此类推。
void TreeLevelOrder(BTNode* root)
{
Queue q;//创建队列
QueueInit(&q);//初始化队列
QueuePush(&q, root);//插入第一个节点
while (!QueueEmpty(&q))//若队列不为空则继续
{
BTNode* front = QueueFront(&q);//获取队列中第一个节点
QueuePop(&q);//删除队列中第一个节点
//若该节点的左、右子节点不为空则将该子节点入队列
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
printf("%d ", front->val);
}
QueueDestroy(&q);
}(7)判断一棵树是否为完全二叉树
思路:完全二叉树特点:当遇到空节点时后面不能有非空节点。
利用层序遍历的方式将树中节点依次插入队列,包括空节点,当向后访问队列遇到空节点时停止插入,并检查队列中剩余节点是否存在非空节点。
bool isCompleteTree(BTNode* root)
{
Queue q;
QueueInit(&q);
QueuePush(&q, root);
//将节点遍历进队列
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
break;
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
//检查队列内剩余元素是否存在非空
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}




















 534
534

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








