How Far Is Video Generation from World Model: A Physical Law Perspective 翻译

Doc2X | 专注学术文档翻译
支持 PDF 转 Word、多栏识别和沉浸式双语翻译，为您的论文处理和学术研究提供全方位支持。
Doc2X | Academic Document Translation Expert
Support PDF to Word, multi-column recognition, and immersive bilingual translation for comprehensive academic research assistance.
👉 了解 Doc2X 功能 | Learn About Doc2X

原文地址 https://arxiv.org/pdf/2411.02385

How Far Is Video Generation from World Model: A Physical Law Perspective

视频生成与世界模型的距离：物理法则的视角

Bingyi Kang* 1 Yang Yue* 1,2

Gao Huang2

• Equal Contribution (in alphabetical order)

• 平等贡献（按字母顺序）

1 Bytedance Research2Tsinghua University3Technion

1 字节跳动研究2 清华大学3 以色列理工学院

Website: https://phyworld.github.io

网站：https://phyworld.github.io

ABSTRACT

摘要

OpenAI’s Sora highlights the potential of video generation for developing world models that adhere to fundamental physical laws. However, the ability of video generation models to discover such laws purely from visual data without human priors can be questioned. A world model learning the true law should give predictions robust to nuances and correctly extrapolate on unseen scenarios. In this work, we evaluate across three key scenarios: in-distribution, out-of-distribution, and combinatorial generalization. We developed a 2D simulation testbed for object movement and collisions to generate videos deterministically governed by one or more classical mechanics laws. This provides an unlimited supply of data for large-scale experimentation and enables quantitative evaluation of whether the generated videos adhere to physical laws. We trained diffusion-based video generation models to predict object movements based on initial frames. Our scaling experiments show perfect generalization within the distribution, measurable scaling behavior for combinatorial generalization, but failure in out-of-distribution scenarios. Further experiments reveal two key insights about the generalization mechanisms of these models: (1) the models fail to abstract general physical rules and instead exhibit “case-based” generalization behavior, i.e., mimicking the closest training example; (2) when generalizing to new cases, models are observed to prioritize different factors when referencing training data: color $>$ size $>$ velocity $>$ shape. Our study suggests that scaling alone is insufficient for video generation models to uncover fundamental physical laws, despite its role in Sora’s broader success.

OpenAI 的 Sora 突出了视频生成在开发遵循基本物理法则的世界模型方面的潜力。然而，视频生成模型是否能够仅凭视觉数据而不依赖人类先验知识来发现这些法则是值得质疑的。一个学习真实法则的世界模型应该能够对细微差别做出稳健的预测，并在未见场景中正确推断。在本研究中，我们在三个关键场景中进行了评估：分布内、分布外和组合泛化。我们开发了一个二维模拟测试平台，用于对象运动和碰撞，以生成由一个或多个经典力学法则确定的视频。这为大规模实验提供了无限的数据供应，并使我们能够定量评估生成的视频是否遵循物理法则。我们训练了基于扩散的视频生成模型，以根据初始帧预测对象运动。我们的规模实验显示，在分布内完美泛化，组合泛化的可测量规模行为，但在分布外场景中失败。进一步的实验揭示了关于这些模型泛化机制的两个关键见解：（1）模型未能抽象出一般物理规则，而是表现出“基于案例”的泛化行为，即模仿最接近的训练示例；（2）在泛化到新案例时，模型在参考训练数据时优先考虑不同的因素：颜色 $>$ 尺寸 $>$ 速度 $>$ 形状。我们的研究表明，仅靠规模不足以使视频生成模型揭示基本物理法则，尽管它在 Sora 更广泛的成功中发挥了作用。

1 INTRODUCTION

1 引言

Foundation models (Bommasani et al., 2021) have emerged remarkable capabilities by scaling the model and data to an unprecedented scale (Brown, 2020; Kaplan et al., 2020). As an example, OpenAI’s Sora (Brooks et al., 2024) not only generates high-fidelity and surreal videos, but also has sparked a new surge of interest in studying world models (Yang et al., 2023).

基础模型（Bommasani et al., 2021）通过将模型和数据规模扩大到前所未有的规模，展现出了显著的能力（Brown, 2020; Kaplan et al., 2020）。例如，OpenAI 的 Sora（Brooks et al., 2024）不仅生成高保真和超现实的视频，还引发了对世界模型研究的新一轮兴趣（Yang et al., 2023）。

“Scaling video generation models is a promising path towards building general purpose simulators of the physical world.” - Sora Report (Brooks et al., 2024)

“扩展视频生成模型是构建物理世界通用模拟器的有前景的路径。” - Sora 报告（Brooks et al., 2024）

World simulators are receiving broad attention from robotics (Yang et al., 2023) and autonomous driving (Hu et al., 2023) for the ability to generate realistic data and accurate simulations. These models are required to comprehend fundamental physical laws to produce data that extends beyond the training corpus and to guarantee precise simulation. However, it remains an open question whether video generation can discover such rules merely by observing videos, as Sora does. We aim to provide a systematic study to understand the critical role and limitation of scaling in physical law discovery.

世界模拟器因其生成真实数据和准确模拟的能力，正受到机器人技术（Yang et al., 2023）和自动驾驶（Hu et al., 2023）的广泛关注。这些模型需要理解基本的物理法则，以生成超出训练语料库的数据，并确保精确的模拟。然而，视频生成是否仅通过观察视频就能发现这些规则仍然是一个未解的问题，正如 Sora 所做的那样。我们旨在提供系统的研究，以理解扩展在物理法则发现中的关键作用和局限性。

It is challenging to determine whether a video model has learned a law instead of merely memorizing the data. Since the model’s internal knowledge is inaccessible, we can only infer the model’s understanding by examining its predictions on unseen scenarios, i.e., its generalization ability. We propose a categorization (Figure 1) for comprehensive evaluation based on the relationship between training and testing data in this paper. In-distribution (ID) generalization assumes that training and testing data are independent and identically distributed (i.i.d.). Out-of-distribution (OOD) generalization, on the other hand, refers to the model’s performance on testing data that come from a different distribution than the training data, particularly when latent parameters fall outside the range seen during training. Human-level physical reasoning can easily extrapolate OOD and predict physical processes without encountering the exact same scenario before. Additionally, we also examine a special OOD capacity called combinatorial generalization, which assesses whether a model can combine two distinct concepts in a novel way, a trait often considered essential for foundation models in advancing toward artificial general intelligence (AGI) (Du & Kaelbling, 2024).

确定一个视频模型是否学习了规律而不仅仅是记忆数据是具有挑战性的。由于模型的内部知识不可访问，我们只能通过检查模型在未见场景上的预测，即其泛化能力，来推断模型的理解。我们在本文中提出了一种分类方法（图1），用于基于训练数据和测试数据之间的关系进行全面评估。分布内（ID）泛化假设训练数据和测试数据是独立同分布（i.i.d.）。而分布外（OOD）泛化则指模型在来自不同于训练数据分布的测试数据上的表现，特别是在潜在参数超出训练期间所见范围时。人类级别的物理推理可以轻松地进行OOD外推，并在未曾遇到完全相同的场景之前预测物理过程。此外，我们还考察了一种特殊的OOD能力，称为组合泛化，它评估模型是否能够以新颖的方式结合两个不同的概念，这一特征通常被认为是基础模型在向人工通用智能（AGI）发展过程中至关重要的（Du & Kaelbling, 2024）。

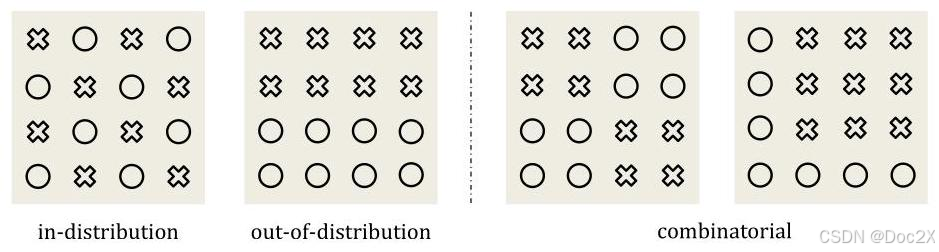
Figure 1: Categorization of generalization patterns. $○$ denotes training data. $\times$ denotes testing data.

图1：泛化模式的分类。$○$ 表示训练数据。$\times$ 表示测试数据。

Moreover, real-world videos typically contain complex, non-rigid objects and motions, which present significant challenges for quantitative evaluation and even human validation. The rich textures and appearances in such videos can act as confounding factors, distracting the model from focusing on the underlying physics. To mitigate these issues, we specifically focus on classical mechanics and develop a 2D simulator with objects represented by simple geometric shapes. Each video depicts the motion or collision of these 2D objects, governed entirely by one or two fundamental physical laws, given the initial frames. This simulator allows us to generate large-scale datasets to support the scaling of video generation models. Additionally, we have developed a tool to infer internal states (e.g., the position and size) of each object in the generated video from pixels. This enables us to establish quantitative evaluation metrics for physical law discovery.

此外，现实世界的视频通常包含复杂的非刚性物体和运动，这给定量评估甚至人工验证带来了重大挑战。这些视频中的丰富纹理和外观可能成为混淆因素，使模型无法专注于潜在的物理规律。为了解决这些问题，我们特别关注经典力学，并开发了一个二维模拟器，其中的物体由简单的几何形状表示。每个视频描绘了这些二维物体的运动或碰撞，完全由一到两个基本物理定律支配，基于初始帧。这个模拟器使我们能够生成大规模数据集，以支持视频生成模型的扩展。此外，我们还开发了一种工具，可以从像素中推断生成视频中每个物体的内部状态（例如，位置和大小）。这使我们能够建立物理定律发现的定量评估指标。

We begin by investigating how scaling video generation models affects ID and OOD generalization. We select three fundamental physical laws for simulation: uniform linear motion of a ball, perfectly elastic collision between two balls,and parabolic motion of a ball. We scale the dataset from $30\mathrm{K}$ to 3 million examples and increase the video diffusion model’s parameters from 22M to 310M. Consistently, we observe that the model achieves near-perfect ID generalization across all tasks. However, the OOD generalization error does not improve with increased data and model size, revealing the limitations of scaling video generation models in handling OOD data. For combinatorial generalization, we design an environment that involves multiple objects undergoing free fall and collisions to study their interactions. Every time, four objects from eight are selected to create a video. In total,70 combinations $\left(C_8^4\right)$ are possible. We use 60 of them for training and 10 for testing. We train models by varying the number of training data from $600\mathrm{K}$ to $6\mathrm{M}$ . We manually evaluate the generated test samples by labeling them as “abnormal” if the video looks physically implausible. The results demonstrate that scaling the data substantially reduces the percentage of abnormal cases, from $67\%$ to $10\%$ . This suggests that scaling is critical for improving combinatorial generalization.

我们首先研究视频生成模型的规模如何影响 ID 和 OOD 泛化。我们选择三条基本物理定律进行模拟：球的匀速直线运动、两个球之间的完全弹性碰撞，以及球的抛物运动。我们将数据集从 $30\mathrm{K}$ 扩展到 300 万个示例，并将视频扩散模型的参数从 2200 万增加到 3.1 亿。我们一致观察到，模型在所有任务中实现了近乎完美的 ID 泛化。然而，OOD 泛化误差并未随着数据和模型规模的增加而改善，这揭示了在处理 OOD 数据时扩展视频生成模型的局限性。对于组合泛化，我们设计了一个涉及多个物体自由下落和碰撞的环境，以研究它们的相互作用。每次从八个物体中选择四个来创建一个视频。总共有 70 种组合 $\left(C_8^4\right)$ 是可能的。我们使用其中的 60 种进行训练，10 种进行测试。我们通过改变训练数据的数量从 $600\mathrm{K}$ 到 $6\mathrm{M}$ 来训练模型。我们通过将生成的测试样本标记为“异常”来手动评估它们，如果视频看起来在物理上不合理。结果表明，扩展数据显著减少了异常案例的百分比，从 $67\%$ 降低到 $10\%$。这表明扩展对于改善组合泛化至关重要。

Our empirical analysis reveals two intriguing properties of the generalization mechanism in video generation models. First, these models can be easily biased by “deceptive” examples from the training set, leading them to generalize in a “case-based” manner under certain conditions. This phenomenon, also observed in large language models (Hu et al., 2024), describes a model’s tendency to reference similar training cases when solving new tasks. For instance, consider a video model trained on data of a high-speed ball moving in uniform linear motion. If data augmentation is performed by horizontally flipping the videos, thereby introducing reverse-direction motion, the model may generate a scenario where a low-speed ball reverses direction after the initial frames, even though this behavior is not physically correct. Second, we explore how different data attributes compete during the generalization process. For example, if the training data for uniform motion consists of red balls and blue squares, the model may transform a red square into a ball immediately after the conditioning frames. This behavior suggests that the model prioritizes color over shape. Our pairwise analysis reveals the following prioritization hierarchy: color $>$ size $>$ velocity $>$ shape. This ranking could explain why current video generation models often struggle with maintaining object consistency.

我们的实证分析揭示了视频生成模型中泛化机制的两个有趣特性。首先，这些模型容易受到训练集中“欺骗性”示例的偏见，从而在某些条件下以“案例基础”的方式进行泛化。这一现象在大型语言模型中也有所观察（Hu et al., 2024），描述了模型在解决新任务时倾向于参考相似训练案例的倾向。例如，考虑一个在均匀直线运动中移动的高速球数据上训练的视频模型。如果通过水平翻转视频进行数据增强，从而引入反向运动，模型可能会生成一个低速球在初始帧后反转方向的场景，尽管这种行为在物理上并不正确。其次，我们探讨了在泛化过程中不同数据属性之间的竞争。例如，如果均匀运动的训练数据由红球和蓝方块组成，模型可能会在条件帧之后立即将红方块转换为球。这种行为表明模型优先考虑颜色而非形状。我们的成对分析揭示了以下优先级层次：颜色 $>$ 大小 $>$ 速度 $>$ 形状。这一排名可能解释了当前视频生成模型在保持物体一致性方面常常面临的挑战。

We hope these findings provide valuable insights for future research in video generation and the development of world models.

我们希望这些发现为未来的视频生成研究和世界模型的发展提供有价值的见解。

2 DISCOVERING PHYSICS LAWS WITH VIDEO GENERATION

2 通过视频生成发现物理定律

2.1 Problem Definition

2.1 问题定义

In this section, we aim to establish the framework and define the concept of physical laws discovery in the context of video generation. In classical physics, laws are articulated through mathematical equations that predict future state and dynamics from initial conditions. In the realm of video-based observations, each frame represents a moment in time, and the prediction of physical laws corresponds to generating future frames conditioned on past states.

在这一部分，我们旨在建立框架并定义在视频生成背景下物理定律发现的概念。在经典物理中，定律通过数学方程表达，这些方程根据初始条件预测未来状态和动态。在基于视频的观察领域，每一帧代表一个时间点，物理定律的预测对应于在过去状态的条件下生成未来帧。

Consider a physical procedure which involves several latent variables $\mathbf{z}=\left(z_1,z_2,\dots ,z_k\right)\in \mathcal{Z}\subseteq$ ${\mathbb{R}}^k$ ,each standing for a certain physical parameter such as velocity or position. By classical mechanics, these latent variables will evolve by differential equation $\dot{\mathbf{z}}=F\left(\mathbf{z}\right)$ . In discrete version,if time gap between two consecutive frames is $\delta$ ,then we have ${\mathbf{z}}_{t+1}\approx {\mathbf{z}}_t+\delta F\left({\mathbf{z}}_t\right)$ . Denote rendering function as $R\left(\cdot \right):\mathcal{Z}\mapsto {\mathbb{R}}^{3\times H\times W}$ which render the state of the world into an image of shape $H\times W$ with RGB channels. Consider a video V = { I 1 , I 2 , … , I L } V = \left\{ {{I}_{1},{I}_{2},\ldots ,{I}_{L}}\right\} V={I1​,I2​,…,IL​} consisting of $L$ frames that follows the classical mechanics dynamics. The physical coherence requires that there exists a series of latent variables which satisfy following requirement: 1) ${\mathbf{z}}_{t+1}={\mathbf{z}}_t+\delta F\left({\mathbf{z}}_t\right),t=1,\dots ,L-1$ . 2) $I_t=R\left(z_t\right),t=1,\dots ,L$ . We train a video generation model $p$ parametried by $\theta$ ,where $p_{\theta }\left(I_1,I_2,\dots ,I_L\right)$ characterizes its understanding of video frames. We can predict the subsequent frames by sampling from $p_{\theta }\left(I_{c+1}^{\prime },\dots I_L^{\prime }\mid I_1,\dots ,I_c\right)$ based on initial frames’ condition. The variable $c$ usually takes the value of 1 or 3 depends on tasks. Therefore,physical-coherence loss can be simply defined as $-\log p_{\theta }\left(I_{c+1},\dots ,I_L\mid I_1,\dots ,I_c\right)$ . It measures how likely the predicted value will cater to the real world development. The model must understand the underlying physical process to accurately forecast subsequent frames, which we can quantatively evaluate whether video generation model correctly discover and simulate the physical laws.

考虑一个涉及多个潜在变量的物理过程 $\mathbf{z}=\left(z_1,z_2,\dots ,z_k\right)\in \mathcal{Z}\subseteq$ ${\mathbb{R}}^k$，每个变量代表某个物理参数，如速度或位置。根据经典力学，这些潜在变量将通过微分方程 $\dot{\mathbf{z}}=F\left(\mathbf{z}\right)$ 发展。在离散版本中，如果两个连续帧之间的时间间隔为 $\delta$，那么我们有 ${\mathbf{z}}_{t+1}\approx {\mathbf{z}}_t+\delta F\left({\mathbf{z}}_t\right)$。将渲染函数表示为 $R\left(\cdot \right):\mathcal{Z}\mapsto {\mathbb{R}}^{3\times H\times W}$，它将世界状态渲染为形状为 $H\times W$ 的图像，并具有 RGB 通道。考虑一个由 $L$ 帧组成的视频 V = { I 1 , I 2 , … , I L } V = \left\{ {{I}_{1},{I}_{2},\ldots ,{I}_{L}}\right\} V={I1​,I2​,…,IL​}，该视频遵循经典力学动态。物理一致性要求存在一系列潜在变量，满足以下要求：1) ${\mathbf{z}}_{t+1}={\mathbf{z}}_t+\delta F\left({\mathbf{z}}_t\right),t=1,\dots ,L-1$。2) $I_t=R\left(z_t\right),t=1,\dots ,L$。我们训练一个视频生成模型 $p$，其参数由 $\theta$ 表征，其中 $p_{\theta }\left(I_1,I_2,\dots ,I_L\right)$ 描述其对视频帧的理解。我们可以通过从 $p_{\theta }\left(I_{c+1}^{\prime },\dots I_L^{\prime }\mid I_1,\dots ,I_c\right)$ 中采样来预测后续帧，基于初始帧的条件。变量 $c$ 通常取值为 1 或 3，具体取决于任务。因此，物理一致性损失可以简单地定义为 $-\log p_{\theta }\left(I_{c+1},\dots ,I_L\mid I_1,\dots ,I_c\right)$。它衡量预测值与现实世界发展的契合度。模型必须理解潜在的物理过程，以准确预测后续帧，我们可以定量评估视频生成模型是否正确发现并模拟物理法则。

2.2 Video Generation Model

2.2 视频生成模型

Following Sora (Brooks et al., 2024), we adopt the Variational Auto-Encoder (VAE) and DiT architectures for video generation. The VAE compresses videos into latent representations both spatially and temporally, while the DiT models the denoising process. This approach demonstrates strong scalability and achieves promising results in generating high-quality videos.

根据 Sora (Brooks et al., 2024)，我们采用变分自编码器 (VAE) 和 DiT 架构进行视频生成。VAE 在空间和时间上将视频压缩为潜在表示，而 DiT 则建模去噪过程。这种方法展示了强大的可扩展性，并在生成高质量视频方面取得了良好的结果。

VAE Model. We employ a (2+1)D-VAE to project videos into a latent space. Starting with the SD1.5-VAE structure, we extend it into a spatiotemporal autoencoder using 3D blocks (Yu et al., 2023b). All parameters of the $\left(2+1\right)\mathrm{D}$ -VAE are pretrained on high-quality image and video data to maintain strong appearance modeling while enabling motion modeling. More details are provided in Appendix A.3.1. In this paper, we fix the pretrained VAE encoder and use it as a video compressor. Results in Appendix A.3.2 confirm the VAE’s ability to accurately encode and decode the physical event videos. This allows us to focus solely on training the diffusion model to learn the physical laws.

VAE 模型。我们采用 (2+1)D-VAE 将视频投影到潜在空间。从 SD1.5-VAE 结构开始，我们将其扩展为一个时空自编码器，使用 3D 块 (Yu et al., 2023b)。所有 $\left(2+1\right)\mathrm{D}$ -VAE 的参数都在高质量图像和视频数据上进行预训练，以保持强大的外观建模，同时启用运动建模。更多细节见附录 A.3.1。在本文中，我们固定预训练的 VAE 编码器，并将其用作视频压缩器。附录 A.3.2 的结果确认了 VAE 准确编码和解码物理事件视频的能力。这使我们能够专注于训练扩散模型，以学习物理法则。

Diffusion model. Given the compressed latent representation from the VAE model, we flatten it into a sequence of spacetime patches, as transformer tokens. Notably, self-attention is applied to the entire spatio-temporal sequence of video tokens, without distinguishing between spatial and temporal dimensions. For positional embedding, a 3D variant of RoPE (Su et al., 2024) is adopted. As stated in Sec.2.1,our video model is conditioned on the first $c$ frames. The $c$ -frame video is zero-padded to the same length as the full physical video. We also introduce a binary mask “video” by setting the value of the first $c$ frames to 1,indicating those frames are the condition inputs. The noise,condition and mask videos are concatenated along the channel dimension to form the final input to the model.

扩散模型。给定来自 VAE 模型的压缩潜在表示，我们将其展平为一系列时空补丁，作为变换器令牌。值得注意的是，自注意力应用于整个视频令牌的时空序列，而不区分空间和时间维度。对于位置嵌入，采用 RoPE 的 3D 变体 (Su et al., 2024)。如第 2.1 节所述，我们的视频模型以前 $c$ 帧为条件。该 $c$ 帧视频被零填充到与完整物理视频相同的长度。我们还通过将前 $c$ 帧的值设置为 1，引入了一个二进制掩码“视频”，表示这些帧是条件输入。噪声、条件和掩码视频沿通道维度连接，形成模型的最终输入。

2.3 ON THE VERIFICATION OF LEARNED LAWS

2.3 关于学习法则的验证

Suppose we have a video generation model learned based on the above formulation. How do we determine if the underlying physical law has been discovered? A well-established law describes the behavior of the natural world, e.g., how objects move and interact. Therefore, a video model incorporating true physical laws should be able to withstand experimental verification, producing reasonable predictions under any circumstances, which demonstrates the model’s generalization ability. To comprehensively evaluate this, we consider the following categorization of generalization (see Figure 1) within the scope of this paper: 1) In-distribution (ID) generalization describes the setting where training data and testing data are from the same distribution. In our case, both training and testing data follow the same law and are located in the same domain. 2) A human who has learned a physical law can easily extrapolate to scenarios that have never been observed before. This ability is referred to as out-of-distribution (OOD) generalization. Although it sounds challenging, this evaluation is necessary as it indicates whether a model can learn principled rules from data. 3) Moreover, there is a situation between ID and OOD, which has more practical value. We call this combinatorial generalization, representing scenarios where every “concept” or object has been observed during training, but not their every combination. It examines a model’s ability to effectively combine relevant information from past experiences in novel ways. A similar concept has been explored in LLMs (Riveland & Pouget, 2024), which demonstrated that models can excel at linguistic instructing tasks by recombining previously learned components, without task-specific experience.

假设我们有一个基于上述公式学习的视频生成模型。我们如何确定是否发现了潜在的物理法则？一个成熟的法则描述了自然界的行为，例如，物体如何运动和相互作用。因此，包含真实物理法则的视频模型应该能够经受实验验证，在任何情况下产生合理的预测，这表明模型的泛化能力。为了全面评估这一点，我们考虑本文范围内的泛化分类（见图1）：1）同分布（ID）泛化描述了训练数据和测试数据来自同一分布的情况。在我们的案例中，训练和测试数据都遵循相同的法则，并位于同一领域。2）一个学习了物理法则的人可以轻松推断出从未观察过的场景。这种能力被称为异分布（OOD）泛化。尽管听起来具有挑战性，但这种评估是必要的，因为它表明模型是否能够从数据中学习原则性规则。3）此外，在ID和OOD之间还有一种情况，具有更实际的价值。我们称之为组合泛化，表示在训练期间观察到的每个“概念”或对象，但并非它们的每种组合的场景。它考察模型以新颖的方式有效结合过去经验中的相关信息的能力。类似的概念已在大型语言模型（LLMs）中探讨（Riveland & Pouget, 2024），表明模型可以通过重新组合先前学习的组件，在没有特定任务经验的情况下，在语言指令任务中表现出色。

3 IN-DISTRIBUTION AND OUT-OF-DISTRIBUTION GENERALIZATION

3 同分布与异分布泛化

In this section, we study how in-distribution and out-of-distribution generalization is correlated with model or data scaling. We focus on deterministic tasks governed by basic kinematic equations, as they allow clear definitions of ID/OOD and straightforward quantitative error evaluation.

在本节中，我们研究了在分布内和分布外的泛化与模型或数据扩展之间的相关性。我们关注由基本运动学方程支配的确定性任务，因为它们允许清晰地定义 ID/OOD，并进行简单的定量误差评估。

3.1 FUNDAMENTAL PHYSICAL SCENARIOS

3.1 基本物理场景

Specifically, we consider three physical scenarios illustrated in Fig. 2. 1) Uniform Linear Motion: A colored ball moves horizontally with a constant velocity. This is used to illustrate the law of Intertia. 2) Perfectly Elastic Collision: Two balls with different sizes and speeds move horizontally toward each other and collide. The underlying physical law is the conservation of energy and momentum. 3) Parabolic Motion: A ball with a initial horizontal velocity falls due to gravity. This represents Newton’s second law of motion. Each motion is determined by its initial frames.

具体而言，我们考虑图 2 中所示的三种物理场景。1) 匀速直线运动：一个彩色球以恒定速度水平移动。这用于说明惯性定律。2) 完全弹性碰撞：两个大小和速度不同的球水平朝彼此移动并发生碰撞。其基本物理定律是能量和动量守恒。3) 抛物运动：一个具有初始水平速度的球因重力而下落。这代表了牛顿第二运动定律。每种运动由其初始框架决定。

Training data generation. We use Box2D to simulate kinematic states for various scenarios and render them as videos, with each scenario having 2-4 degrees of freedom (DoF), such as the balls’ initial velocity and mass. An in-distribution range is defined for each DoF. We generate training datasets of $30\mathrm{K},300\mathrm{K}$ ,and $3\mathrm{M}$ videos by uniformly sampling a high-dimensional grid within these ranges. All balls have the same density, so their mass is inferred from their size. Gravitational acceleration is constant in parabolic motion for consistency. Initial ball positions are randomly initialized within the visible range. Further details are provided in Appendix A.4.

训练数据生成。我们使用 Box2D 来模拟各种场景的运动状态，并将其渲染为视频，每个场景具有 2-4 个自由度（DoF），例如球的初始速度和质量。为每个自由度定义了一个分布内范围。我们通过在这些范围内均匀采样高维网格生成 $30\mathrm{K},300\mathrm{K}$ 和 $3\mathrm{M}$ 视频的训练数据集。所有球的密度相同，因此其质量由其大小推断。为了保持一致性，抛物运动中的重力加速度是恒定的。初始球位置在可视范围内随机初始化。更多细节见附录 A.4。

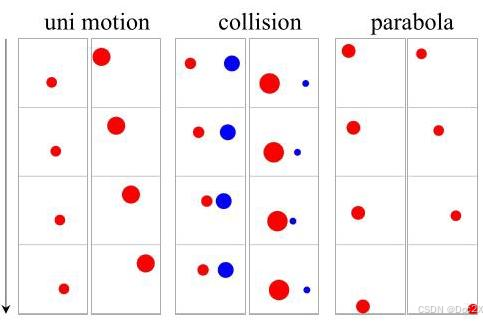
Figure 2: Downsampled video visualization. The arrow indicates the progression of time.

图 2：下采样视频可视化。箭头表示时间的进程。

Test data generation. We evaluate the trained model using both ID and OOD data. For ID evaluation, we sample from the same grid used during training, ensuring that no specific data point is part of the training set. OOD evaluation videos are generated with initial radius and velocity values outside the training range. There are various types of OOD setting, e.g. velocity/radius-only or both OOD. Details are provided in Appendix A.4.

测试数据生成。我们使用 ID 和 OOD 数据评估训练好的模型。对于 ID 评估，我们从训练期间使用的相同网格中采样，确保没有特定数据点属于训练集。OOD 评估视频是通过初始半径和速度值生成的，这些值超出了训练范围。OOD 设置有多种类型，例如仅速度/半径或两者均为 OOD。详细信息见附录 A.4。

Table 1: Details of DiT model sizes.

表 1：DiT 模型大小的详细信息。

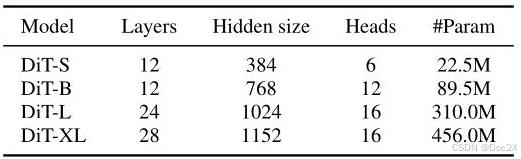
Models. For each scenario, we train models of varying sizes from scratch, as shown in Table 1. This ensures that the outcomes are not influenced by uncontrollable pretrain data. The first three frames are provided as conditioning, which is sufficient to infer the velocity of the balls and predict the subsequent frames. Diffusion model is trained for $100\mathrm{K}$ steps using 32 Nvidia A100 GPUs with a batch size of 256,which was sufficient for convergence,as a model trained for $300\mathrm{K}$ steps achieves a similar performance. We keep the pretrained VAE fixed. Each video consists of 32 frames with a resolution of $128\times 128$ . We also experimented with a $256\times 256$ resolution,which yielded a similar generalization error but significantly slowed down the training process.

模型。对于每种场景，我们从头开始训练不同大小的模型，如表 1 所示。这确保了结果不受不可控的预训练数据影响。前三个帧作为条件输入，这足以推断球的速度并预测后续帧。扩散模型在 $100\mathrm{K}$ 步骤中使用 32 个 Nvidia A100 GPU 进行训练，批量大小为 256，这对于收敛是足够的，因为训练 $300\mathrm{K}$ 步骤的模型达到了类似的性能。我们保持预训练的 VAE 固定。每个视频由 32 帧组成，分辨率为 $128\times 128$。我们还尝试了 $256\times 256$ 分辨率，这产生了类似的泛化误差，但显著减慢了训练过程。

Evaluation metrics. We observed that the learned models are able to generate balls with consistent shapes. To obtain the center positions of the $i$ -th ball in the generated videos, $x_t^i$ ,we use a heuristic

评估指标。我们观察到学习到的模型能够生成形状一致的球体。为了获得生成视频中第 $i$ 个球的中心位置，$x_t^i$，我们使用了一种启发式方法。

—— 更多内容请到Doc2X翻译查看——
—— For more content, please visit Doc2X for translations ——