滴滴因果建模新突破：最优传输+表征学习攻克长期效应估计难题​

背景

近年来，基于观测数据的因果推断在补贴定价等领域得到广泛的应用，其旨在评估不同处理变量（ Treatment，例如优惠券金额）对结果变量（Outcome，例如GMV）所能带来的处理效应（Treatment effect），进而我们能够根据不同处理效应选择最优的处理变量。在网约车市场下，我们常常关注短期处理效应和长期处理效应：

• 针对短期处理效应，已经有许多成熟的模型可以使用，例如DML、GRF、CFR等。

• 针对长期处理效应，我们发现现有方法难以直接应用在复杂的商业环境下。因为现有方法依赖于理想假设（二元策略变量或不存在未观测混淆变量）去估计长期平均处理效应（Long-term average treatment effect）。然而，在真实市场环境下，上述理想假设容易被违背，同时平均层面的长期处理效应不足以提供个性化的决策。

本文旨在解决更普遍的长期处理效应估计问题，即在考虑连续处理变量和未观测混淆存在的情况下，估计长期异质性剂量-响应曲线（Long-term Heterogeneous Dose-Response Curve，简写为Long-term HDRC)。本文将对滴滴在这一领域内的研究成果做一个简单介绍，更多内容详见论文[1]。

上述Long-term HDRC的估计问题存在以下两大挑战：

• 目标估计量的可识别性问题。该问题主要是因为长期历史观测数据存在未观测混淆变量，导致可识别性假设不满足。因此研究如何引入短期随机试验数据，通过数据融合的方式消除长期历史观测数据中未观测混淆的影响，是我们首要解决的问题。

• 反事实估计误差的问题。该问题主要是因为连续处理变量导致反事实空间巨大，若简单拟合长期历史观测数据这一事实数据，学到的估计器很难有效泛化到反事实空间。因此如何推导Long-term HDRC下的反事实估计泛化界限，并基于此设计估计器，是我们面临的第二个问题。

问题设定

我们使用符号A表示一维的连续处理变量，X表示可观测的混淆变量，U表示未观测的混淆变量，S(a)表示不同时间步

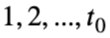
下的潜在短期结果向量，Y(a)表示时间步T下的潜在长期结果。使用大写字母表示随机变量，小写字母表示随机变量的取值。考虑数据融合的场景，即拥有大量的长期历史观测数据

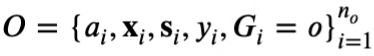
和少量的短期随机试验数据

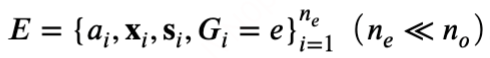
引入

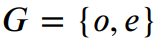
作为数据集的指示变量。注意两类数据中均包含处理变量A、混淆变量X及短期结果S，而长期结果Y仅存在于长期历史观测数据中。基于这两份数据，我们的目标是学习估计器以无偏估计个体在不同处理变量下的长期结果，即长期异质性剂量-响应曲线（Long-term HDRC）：

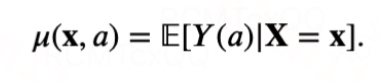
目标估计量Long-term HDRC无法单独从短期随机试验数据或长期历史观测数据识别，因为前者缺失长期结果Y，后者存在未观察到的混淆变量U。为此，我们提出基于数据融合的长期异质性剂量-响应曲线估计框架，除了经典的SUTVA（假设1）和Overlap（假设2）之外，还需要以下关键假设：

• 假设3: 对于观测数据，给定全部混淆变量X和U，处理变量A和潜在结果S(a), Y(a)独立，形式化地，有

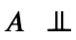
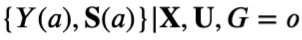
      且

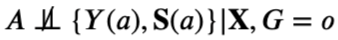
• 假设4: 对于实验数据，仅给定可观测混淆变量X，处理变量A和潜在结果S(a), Y(a)独立，形式化地，有

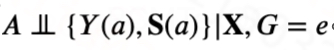
• 假设5: 给定可观察的混淆变量X，潜在结果S(a), Y(a)的分布在实验数据和观测数据中保持一致，形式化地，有

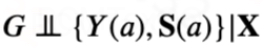
• 假设6: 对于观测数据，给定可观察的混淆变量X和潜在短期结果S(a)，处理变量A与长期潜在结果Y(a)相互独立，形式化地，有

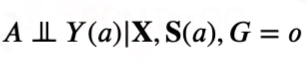
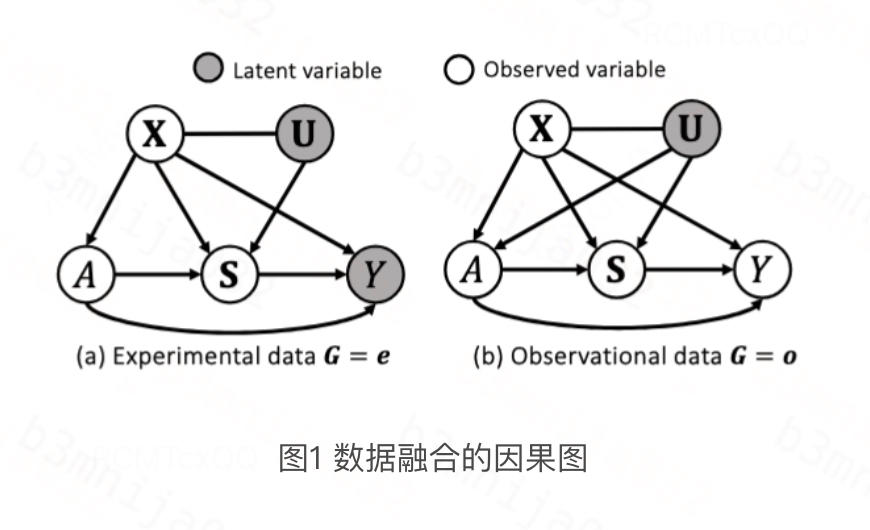
假设1～4都是因果推断领域常见的假设。假设5保证不同数据类型𝐺之间潜在结果的条件分布相同，这个假设是合理的，因为实验数据和观察数据之间的差异通常是处理分配机制，而潜在结果分布保持不变且稳定；假设6未观测混淆U的影响被短期结果S所阻断，即不存在U->Y的边，该假设最初由Susan Athey在[2]中提出以实现二元处理变量下长期平均处理效应的识别，在本文我们重新利用该假设实现更复杂的Long-term HDRC识别。满足上述假设的因果图如下所示：

理论框架

挑战一：目标估计量的可识别性

为了实现目标估计量的可识别性，首先需要解决长期历史观测数据中未观测混淆的影响。在本小节，在理论上提出一种新颖的加权方案使得目标估计量Long-term HDRC可识别，接着提出一种带有理论保证且计算高效的最优传输（Optimal Transport, OT）方法，通过数据融合学习所需要的权重。

基于重加权的可识别性

我们发现，尽管未观测混淆U不可见，但其影响可以通过给定可观测混淆X和处理变量A条件下，指示变量G和短期结果S之间的相关性来捕获，因此基于下述命题和定理，可以实现目标估计量的可识别性：

命题1: 在假设1～6成立的情况下，给定一组权重

其中包含观察样本的可学习权重

和实验样本的均匀权重

满足

即

则在观测数据的重加权分布上，

成立。

定理1: 在命题1成立的情况下，我们有

即目标估计量Long-term HDRC可识别。

上述命题和定理表明，表明如果能够学习合适的权重，使得

那么观测数据中未观测混淆变量的影响将被消除，从而保证Long-term HDRC可以被识别。因此，我们现在的目标是学习一组观察样本的权重

使得基于重加权后的分布满足条件独立性

即

学习最优传输权重

基于上述理论分析，我们采用最优传输方法学习观测样本的权重

即通过最小化条件最优传输距离

学习上述权重。求解条件最优传输距离的最直观方法是对于每个取值组合。

优化每个子问题如下所示：

然而，直接求解上述条件最优传输问题在实践中不可行，原因在于条件集(X, A)通常为高维连续变量，从而导致上述优化问题中包含无穷多个子优化问题。为此，我们建立了条件分布之间的最优传输距离与联合分布之间最优传输距离之间的关系，并给出如下定理：

定理2: 假设联合分布

的成本矩阵是可分离的，即

那么有

定理2表明，条件最优传输距离可以通过相应的联合分布的最优传输距离来界定，这启发我们可以将优化目标从直接最小化难以计算的

转化为优化其上界

从而学习权重

尽管上述理论为条件最优传输问题提供了有效解法，但在实际计算中仍面临严峻的效率挑战。

具体的，直接优化

需要构建并求解完整的传输矩阵

这在大规模数据场景下代价极高，比如历史观测数据的样本量往往非常大。

更为重要的是，这一全局矩阵优化方式与当前主流的深度学习框架不兼容，后者普遍依赖mini-batch训练策略。为克服上述难题，受到[3]的启发，我们提出了一种基于随机采样的小批量最优传输方法如下：

定义1: 设

和

为两个经验分布，分别包n和m个样本。令

的小批量样本数为b，其中b | n，共划分为k=n/b个小批量。记

为

中第i个小批量的样本索引集合，对应的经验分布为

则小批量最优传输（m-OT）定义为：

定理3:令

为

的第i批次对应的最优传输概率矩阵。通过将

扩展为与全局传输矩阵维度一致的

矩阵

不属于

的行填充为零，有：

并且

定理3意味着观测数据与实验数据之间的联合分布

的最优传输距离的上界是相应的m-OT问题。解决m-OT问题不仅显著减少了高优化成本，还允许将最优传输距离嵌入到深度学习框架中，因为其在每次训练迭代时仅考虑批量观测样本和全量实验样本。至此，通过定理2和定理3，分别解决了条件最优传输距离难以直接优化以及全局计算复杂度过高的两大挑战。结合这两个定理，可以通过直接最小化。

学习权重，其为原始条件最优传输距离

的有效上界。因此，估计的权重

可以近似实现命题1，从而根据定理1实现HDRC的可识别性。

挑战二：反事实误差泛化界限

理想情况下，通过学习最优传输引导下的权重

能够有效消除未观察到的混淆偏差，从而实现Long-term HDRC的可识别性。然而，在实际估计HDRC时，反事实预测误差仍然可能较大。主要原因在于模型的训练仅基于观测到的事实结果，无法获取对应的反事实结果。考虑到连续处理的情形下反事实空间是无限的，同时由于

可观测的混淆偏差依然存在，使得反事实预测任务更加复杂。

为了解决上述问题，在最优传输导出的重加权观测数据分布下，推导了反事实预测误差的泛化界限如下，这是后续设计模型的关键

定理4: 假设存在一个函数族

并且存在常数

使得

那么有：

其中

是为选定的

的积分概率度，P(Z)和P(Z, A)是由表征映射

从P(X)和P(X, A)导出的分布。

定理4表明，反事实误差

的上界由实际误差

加上一个重加权的IPM项构成，该IPM项衡量了处理变量A与混淆变量X之间的相关性。该定理启发了基于深度学习的经典平衡表征方法，通过学习平衡表征

来消除可观测的混淆偏差，使得表征与处理A独立，即

模型结构

基于理论框架，通过重加权和表征学习分别解决未观测的和可观测的混淆偏差。本小节总结我们的模型LEARN（Long-term hEterogeneous dose-response curve estimAtor with Reweighting and represeNtation learning), 如图2所示，LEARN由三大模块组成：OT加权模块，平衡表征模块和长期估计模块。

OT加权模块：

该模块基于定理2和3设计，旨在估计权重

以去除未观测的混淆偏差。为了将小批量OT问题

嵌入到深度学习框架中，参考[3]，通过最小化逐批观测数据和全量实验数据之间的

来学习权重

同时为了避免稀疏解，提高求解效率，我们参考[4]对边际分布

施加负熵正则化约束，并通过投影梯度下降来求解下面的最优传输问题：

其中

是熵正则化系数

是构建的成本矩阵。

平衡表征模块：

该模块基于定理4设计，旨在通过平衡表征修正可观测的混淆偏差。在每次迭代中，首先将观察到的混淆变量X输入MLP，并通过最小化

来学习平衡表征Z。在实践中，我们使用Wasserstein距离作为IPM项的实现。

长期估计模块：

该模块旨在根据不同样本的潜在短期结果S(a)来估计潜在的长期结果Y(a)。

参考LTEE[5] 结构来建模短期和长期结果之间的关系。具体的，平衡表征Z首先被输入到GRU q(.)中，以获取每个时间步t的短期表征

然后我们利用一个共享的MLP g(.)预测每个时间步相应的短期结果

之后，利用注意力机制 f(.) 将短期表征集合

映射到长期表征

最后使用另一个MLP h(.)基于长期表征预测长期结果

然而，原始的LTEE[5] 仅适用于二元处理变量，为此使用变系数结构[6] 将上述四个网络 q(.), g(.), f(.), h(.)拓展到连续处理变量场景，以避免单维的处理变量信息被淹没在高维混淆变量的问题。

损失函数：LEARN在每次迭代中的损失函数为：

注意，为了充分利用数据集，额外使用了短期随机试验数据中的短期结果来训练模型。

评估

模拟数据实验

首先在生成数据和半生成数据（News、TCGA）上验证模型LEARN的有效性，使用测试集上Long-term HDRC的MISE作为评估指标，其中s为测试集的样本量，[a1, a2]是处理变量的采样区间。

实验结果如下所示，表明模型相比于基线方法有不错的提升：

在生成数据上使用HSIC量化了混淆偏差的消除程度：平衡表征模块能够消除83.45%的可观测混淆偏差，OT权重模块能够消除70%左右的未观测混淆偏差。

此外，还探究了m-OT问题中批量大小的影响、实验数据样本量的影响以及模型超参数的敏感性影响，具体结果可参见论文[1]。

真实数据实验 

我们已经在滴滴真实定价场景下验证了模型的有效性，通过加入上述长期效应模型来优化策略，可以改善司乘长期留存，AB实验结果表明新模型在长期表现上，GMV、呼叫、TSH等核心指标上均有显著提升。

总结

本文系统解决了连续处理变量与存在未观察到的混淆变量的情况下，通过数据融合估计Long-term HDRC的问题，这在现有研究中尚未得到充分解决。具体的，为了消除未观察混淆变量并使得Long-termHDRC可识别，本文首先在理论上提出了一种新颖的加权方案，并基于最优传输框架设计了一种高效的权重学习方法。

进一步地，为了消除可观测混淆偏差。本文基于最优传输导出的重加权分布推导了反事实结果回归误差的泛化界限。基于上述理论结果，本文设计了模型LEARN来准确地估计Long-term HDRC。大量的模拟数据实验和真实数据实验验证了我们方法的有效性。

参考文献

[1] Yang Z, Chen W, Cai R, et al. Estimating long-term heterogeneous dose-response curve: Generalization bound leveraging optimal transport weights[J]. arXiv preprint arXiv:2406.19195, 2024.

[2] Athey S, Chetty R, Imbens G. Combining experimental and observational data to estimate treatment effects on long term outcomes[J]. arXiv preprint arXiv:2006.09676, 2020.

[3] Yang Y, Gu X, Sun J. Prototypical partial optimal transport for universal domain adaptation[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2023, 37(9): 10852-10860.

[4] Yan Y, Yang Z, Chen W, et al. Exploiting geometry for treatment effect estimation via optimal transport[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2024, 38(15): 16290-16298.

[5] Cheng L, Guo R, Liu H. Long-term effect estimation with surrogate representation[C]//Proceedings of the 14th ACM international conference on web search and data mining. 2021: 274-282.

[6] Nie L, Ye M, Nicolae D. VCNet and Functional Targeted Regularization For Learning Causal Effects of Continuous Treatments[C]//International Conference on Learning Representations.

   欢迎感兴趣的同学一起加入我们

可投递您的简历至

stevenxujixing@didiglobal.com

zhenpeng@didiglobal.com

团队使命

作为网约车交易市场技术核心团队，我们应用机器学习、运筹优化、因果推断、深度强化学习及生成式AI技术（LLM） ，构建支撑千万级日订单的动态双边市场智能决策系统。通过供需预测建模、动态定价策略、智能补贴分配、生态治理引擎 等策略引擎建设，持续优化平台商业价值与司乘体验，驱动全球领先的出行市场效率革新。

供需调节策略方向的主要工作

负责设计研发面向司乘双边市场的动态定价和跨品类联合补贴策略引擎，涉及的技术方向包括：精细化的时空供需预测建模、针对海量数据的细粒度因果建模、大规模运筹优化与求解算法设计、大规模离线仿真系统设计与研发等。

负责设计研发面向用户长期增长的智能增长营销策略引擎，构建可持续优化的收益管理与增长引擎系统，涉及的技术方向包括：长周期用户价值（LTV）建模、基于强化学习的序列化决策模型设计、大规模运筹优化与收益管理系统设计等。

负责设计研发面向供需调节和用户增长的智能运营系统，构建面向多目标高度封装的全自动智能化的运营引擎，助力网约车业务精细化运营提效。涉及的技术方向包括：不同粒度、周期的时序预测建模、大规模运筹优化求解算法、支持深度人机结合的工业化运营引擎架构。

负责设计研发面向网约车交易场景的司乘生态治理引擎，构建面向不同品类业务特点的判责、治理策略系统，涉及技术包括：多模态深度学习建模、大语言模型技术、原子预测和小样本学习等技术。

基础要求

计算机/运筹学/统计学/应用数学硕士及以上学历。

深入掌握机器学习经典模型算法（统计模型/深度模型）及实际场景落地经验。

精通算法设计与数据结构，具备大规模系统开发能力（Python/Java/Spark）。

出色的复杂问题拆解能力与跨团队协作意识。

核心优势

算法研究：在机器学习、运筹优化、强化学习、因果推断等方向有论文/专利成果。

工程能力：精通Spark/Flink等计算框架，有大数据数据处理经验。

行业经验：具备定价策略/用户增长/智能营销等场景落地经验者优先。

竞赛成就：ACM/ICPC金牌、Kaggle Master等顶尖赛事获奖者。

RAS-AUCC：智能营销Uplift模型多Treatment评估指标改进