第十二节 图和网络

本节将重点关注线性代数的应用，事实上，使用线性代数处理的矩阵都是来自现实问题，描述了问题的拓扑结构，人们在处理问题时，需要用到这些拓扑结构。比如，矩阵的初等行变换可以表示元素或分子之间的化学反应，使其变得更加直观。今天我们将重点讨论应用数学中重要的模型，在离散数学中称为“图”。本章，我们将探索图和矩阵之间的联系（关联矩阵），从 关联矩阵 中推导出 欧姆定律 、 基尔霍夫电流定律 、 欧拉公式，并探究这三者之间的关系。

关联矩阵

上节我们知道图由结点和边组成，可以表示人之间的关系、电话网、互联网等，这里以一个小图为例，如下图：

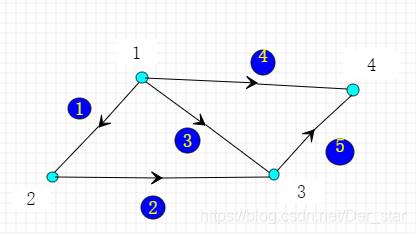
这个图里包含$n=4$个结点，$m=5$条边，我们需要把矩阵写出来做进一步研究，在边上随机加了方向以区分正负（这里我们将图看成电路网络，可以根据方向判断电流的正负，相同为正，相反为负），下面我们构造一个矩阵来解析这个图的含义，称为关联矩阵。在关联矩阵中，每一列代表一个结点，每一行代表一条边（行中的正负代表方向）。易得上（电路网络）图对应的关联矩阵 $A$ 如下：
$$A=\left[\begin{array}{cccc}-1& 1& 0& 0\\ 0& -1& 1& 0\\ -1& 0& 1& 0\\ -1& 0& 0& 1\\ 0& 0& -1& 1\end{array}\right]$$
观察关联矩阵 $A$ 的第一行，第一行代表了电路网络图中边 $1$ 的情况，在图中，边 $1$ 以 点 $1$ 作为起点，以点 $2$ 作为终点，反映到矩阵上就是 $A_{(1,1)}=-1$，$A_{(1,2)}=1$，以此类推。

由图可知，边 $1$，边 $2$，边 $3$ 组成了一个回路，而观察矩阵可发现，这三条边对应的矩阵中的前三行是线性相关的，其中行 $1$ $+$ 行 $2$ $=$ 行 $3$ 。这说明“回路”意味着“相关”，回路对应的行向量组是线性相关的，这是一个图与矩阵之间很巧妙的联系。

关联矩阵源于问题，描述了问题的拓扑结构。一般来说关联矩阵是一个非常稀疏的矩阵，因为它的每行只有两个非零的元素，用于表示起点和终点。
我们已经从实际问题中抽象出相应的关联矩阵，现在我们试图去探究一些关于矩阵的主要问题。

欧姆定律

矩阵得零空间是什么？或者说矩阵的列向量是否是线性无关的？如果线性无关，其零空间只有零向量，否则存在非零向量使得列向量的线性组合为零向量。

要找到零空间，等价于求解$Ax=0$，即：
$$\left[\begin{array}{cccc}-1& 1& 0& 0\\ 0& -1& 1& 0\\ -1& 0& 1& 0\\ -1& 0& 0& 1\\ 0& 0& -1& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right]=0$$
在求解之前我们引入上式的实际意义，将 $x=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right]$ 视为各结点的电势，比如 $x_1$ 表示结点 $1$ 的电势，则：$Ax=\left[\begin{array}{c}{x}_2-x_1\\ x_3-x_2\\ x_3-x1\\ x_4-x_1\\ x_4-x_3\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\end{array}\right]$即为各结点的电势差。
容易求得$A$的零空间为$x=c\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]$，它是一维的直线，这个零空间在现实情况中代表什么呢？这说明如果电势相等（$c$），则不会存在电流。
结点电势由一个常数$c$唯一确定，要求得结点电势就必须确定一个基点，典型的方法是采用接地的方式，这里比如将结点$4$接地，相当于去掉第四列，这样其他三列为线性无关，进而求得其他结点电势。（这就像温度，如果温度相等就不会发生热传导，我们可以通过摄氏温标或绝对温标来测量温度）。

基尔霍夫电流定律

矩阵 $A$ 的左零空间是什么？这相当于求解$A^{T}y=0$

$$\left[\begin{array}{ccccc}-1& 0& -1& -1& 0\\ 1& -1& 0& 0& 0\\ 0& 1& 1& 0& -1\\ 0& 0& 0& 1& 1\end{array}\right]\left[\begin{array}{c}{y}_1\\ y_2\\ y_3\\ y_4\\ y_5\end{array}\right]=\left[\begin{array}{c}-y_1-y_3-y_4\\ y_1-y_2\\ y_2+y_3-y_5\\ y_4+y_5\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]$$
求解前我们先引入上式中 $y$ 的实际意义：将 $y={\left[\begin{array}{ccccc}{y}_1& y_2& y_3& y_4& y_5\end{array}\right]}^T$ 视为各边上的电流 。已知， 电流和电势差的关系服从欧姆定律：边上的电流值是边上电势差的倍数，这个倍速就是边的电导即电阻的倒数，我们把这个常数视为一个系数矩阵记为 $C$。于是：
$$y=\left[\begin{array}{c}{y}_1\\ y_2\\ y_3\\ y_4\\ y_5\end{array}\right]=C\left[\begin{array}{c}{x}_2-x_1\\ x_3-x_2\\ x_3-x1\\ x_4-x_1\\ x_4-x_3\end{array}\right]$$

然后我们观察 $A^{T}y=0$ 中的方程，比如第一个方程 $-y_1-y_3-y_4=0$，这个方程是关于结点 $1$ 上的电流的，方程指出结点 $1$ 上的电流之和为零。

实际上， $A^{T}y=0$ 阐述了基尔霍夫电流定律（Kirchoff’s Current Law​，简称 $KCL$），基尔霍夫电流定律是一个平衡方程，守恒定律，它说明了流入等于流出，电荷在结点上不会积累。

现在，我们开始求解 $y$。 $A$ 的左零空间的维数为 $m-r=2$，这也即左零空间的基有两个向量。

假设 $y_1=1$，也即 $1A$ 的电流在边 $1$ 上流动，那么由图（或者方程）可知 $y_2=1$。为符合基尔霍夫电流定律，那么只需再令 $y_3=-1$ ，也即让 $1A$ 的电流从结点 $2$ 流回结点 $1$，此时令 $y_4=y_5=0$，即可得到一个符合$KCL$的向量 ${\left[\begin{array}{ccccc}1& 1& -1& 0& 0\end{array}\right]}^T$。容易发现，该解发生在结点 $1\to 2\to 3$ 组成的回路中。

同理，我们也容易得到发生在结点 $1\to 3\to 4$ 组成的回路中的解 ${\left[\begin{array}{ccccc}0& 0& 1& -1& 1\end{array}\right]}^T$，该解显然也符合$KCL$。

注意到，这两个从最小回路得到的向量彼此线性无关，这两个向量所组成的向量组恰好就是 $A$ 的左零空间的基。显然，我们似乎找到了一种捷径去求解关联矩阵的左零空间：借助图中的最小回路可以快速求得左零空间的基（注意是最小回路，这样可以确保每个回路所得出的向量之间都是线性无关的，故我们也称线性无关回路），我们把最小回路数记为$\#loops$，有以下等式成立:
$$dimN(A^T)=m-r=\#loops\text{\hspace{1em}(1)}$$

我们再看 $1\to 2\to 3\to 4$ 组成的大回路上，得到符合$KCL$ 的向量 ${\left[\begin{array}{ccccc}1& 1& 0& -1& 1\end{array}\right]}^T$，恰为上述两个基向量之和。

欧拉公式

矩阵 $A$ 的行空间是什么？这也即求 $A^T$ 的列空间。

在上文求 $A$ 的左零空间时，我们已经知道 $A$ 的秩 $r=3$，所以 $A^T$ 的秩也为 $3$。对 $A^T$ 消元可知，其列 $1,2,4$ 为主列。而在电路图中，这三列对应的三条边恰好是没有回路的，同时注意到列 $1,2,3$ 线性相关，在电路图中，这三列对应的三条边存在回路，于是可知，线性相关 / 无关性与回路有关，线性相关等价于存在回路，线性无关等价于没有回路。一般，我们把没有回路的图称为树。

通过探究矩阵 $A$ 的行空间，我们发现 $A^T$ 的秩与图存在的联系：矩阵的秩为 $r$ ，则图中有 $r$ 个线性无关的边，转换成图的语言那就是图中的 $r$ 个边构成了该图的最大无回路。这里需要思考最大无回路的概念，就连通图而言，如果该图存在 $n$ 个结点，那么该图的最大无回路应该包括了 $n-1$ 条边，这条性质是很自然的，因为只要再多一条边，那么就会构成回路，从而线性相关。于是，我们可以得到，矩阵的秩 $r$ = 图中的结点数 $n$ 再减去 $1$。
$$m=\#edges\text{\hspace{1em}(2)}$$
$$r=\#nodes\text{\hspace{1em}(3)}$$

现在我们可以引出 欧拉公式 了。已知：

其中 $\#loops$ 为最小回路数，$\#edges$ 为边数，$\#nodes$ 为结点数，将$(2)(3)$代入到 $(1)$ 中可得 $\#loops=\#edges-(\#nodes-1)$，再整理即：

这也即欧拉公式：$结点数-边数+最小回路=1$

基本方程

综上内容，我们得到应用数学的基本方程的蓝图：
$$\left[\begin{array}{cc}x=\left[\begin{array}{cccc}{x}_1& x_2& x_3& x_4\end{array}\right]:结点电势& A^{T}y=0（KCL定律）\\ \downarrow e=Ax& \uparrow f=A^{T}y\\ x_2-x_1,..等等:各边的电势差& \stackrel{y=Ce（欧姆定率）}{⟶}y={\left[\begin{array}{cccc}{y}_1& y_2& y_3& y_4\end{array}\right]}^T：各边上的电流\end{array}\right]$$

上述三式是在 无外部电源 情况下的方程。

考虑添加外部电源的因素，那么电源可以通过 在边上加电压源 和在点上加电流源 两种方式接入。
如果是在边上加电压源，那么会直接体现在 $e=Ax$ 的 $e$ 中（边上两点的电势差改变了，$e$ 中的分量会因此改变）。如果是在点上加电流源，那么会直接体现在 $A^{T}y=f$ 的 $f$ 中（点上的电流情况改变了，$f$ 中的分量会因此改变）。

联立上述三个等式 可得 $A^{T}CAx=f$。需要注明的是，该方程作为一个平衡方程仅描述平衡状态，并没有考虑时间，牛顿定律不适用于此。最后，可以看出$A^{T}CA$ 是一个对称矩阵。