本文深入探讨了排序算法的时间复杂度，包括选择排序、冒泡排序及其优化，以及插入排序。分析了这些算法的步骤、代码实现，并通过实例解释了时间复杂度为O(log(N^2))的原理。此外，还涉及到了异或运算在寻找数组中单数元素的应用，以及二分法在解决局部最小值问题上的应用。
目录
4.1.1 题目：一组数只有一个数出现奇数次，其他出现偶数次，找出这个出现奇数次的数
4.1.2 一组数只有两个数出现一次，其他出现两次，找出这两个数：
7.1 在一个有序数组中，找一个数是否存在，复杂度少于（O(N))
01 时间复杂度分析
常数时间的操作：一个操作如果和数据量没有关系，每次都是固定时间内完成的操作，叫做常数操作。我的理解是这种操作最终的执行就是执行汇编命令，而汇编命令执行花费的时间都是有限的机器时钟时间，可以简单理解为执行一个相加指令，所以常数操作花费的时间是确定有限的，和数量级没关系。
时间复杂度为一个算法流程中，常数操作数量的指标，常用O（读作 big O）来表示。具体来说，在常数操作数量的表达式中，只要有高阶项，不要低阶项，也不要高阶项的系数，剩下的部分如果记为f(N),那么时间复杂度为O(f(N))。
评价一个算法流程的好坏，先看时间复杂度的指标，然后再分析不同数据样本下的实际运行时间，也就是常数项时间。
- 举例
public class Test {
public void proffessor1(){
int a = 0;
for (int i = 0; i < 1000; i++){
a = 3 + 4;
a = 3 - 5;
a = 3 * 77;
}
}
public void proffessor2(){
int a = 0;
for (int i = 0; i < 1000; i++){
a = 3 ^ 4;
a = 3 & 5;
a = 3 | 77;
}
}
}两个代码时间复杂度相同均为O(N),比较时间复杂度需要比较常数项操作需要时间，即实际运行时间
02 选择排序及时间复杂度分析
第一次从0 .................n-1中选择出最小（大）值放在0
第二次从 1 .................n-1中选择出最小（大）值放在1
第三次从 2 .................n-1中选择出最小（大）值放在2
直到选择完： 等差数列（时间复杂度O（N^2）, 额外空间复杂度O（1））
2.1 算法步骤
首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
重复第二步，直到所有元素均排序完毕。
2.2 代码实现
import java.util.Arrays;
public class SelectionSort {
public static void SelectionSort(int[] arr){
// 首先判断输入合法性
if(arr == null || arr.length < 2){
System.out.println("不需要排序");
return;
}
for(int i = 0; i < arr.length - 1; i ++){
int minIndex = i;
for(int j = i + 1; j < arr.length; j++){
if(arr[minIndex] > arr[j]){
minIndex = j;
}
}
swap(arr, i, minIndex);
}
}
public static void swap(int[] arr, int i, int j){
if(i != j){
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
}
public static void main(String[] args){
int[] arr = new int[]{3,5,2,-2,7,9,-10};
SelectionSort(arr);
System.out.println(Arrays.toString(arr));
}
}03 冒泡排序算法和时间复杂度分析
第一次冒：0 ............. n-1
第二次冒：0 ....... n-2
第三次冒：0 ... n-3
直到冒完，每次比较大的数放在后面（时间复杂度O(N^2), 额外复杂度 O(1)）
3.1 算法步骤
比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
3.2 代码实现
import java.util.Arrays;
public class BubbleSort {
public static void BubbleSort(int[] arr){
if(arr.length < 2 || arr == null){
System.out.println("无需排序");
return;
}
// for(int i = 0; i < arr.lenth - 1; i++){ // 把最大的数排在最后一位
// for(int j = 0; j < arr.lenth - 1 - i; j++){ // 第二大的数排在倒数第二位
for(int e = arr.length - 1; e >= 0; e--){
for(int i = 0 ; i < e; i ++){
if(arr[i] > arr[i + 1]){
swap(arr, i, i +1);
}
}
}
}
public static void swap(int[] arr, int i, int j){
if(i != j){
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
}
public static void main(String[] args){
int[] arr = new int[]{3,5,2,-2,7,9,-10};
BubbleSort(arr);
System.out.println(Arrays.toString(arr));
}
}
3.3 冒泡排序算法的优化
如果在某一趟排序过程中没有发现数据的交换， 则可以提前结束排序过程
04 异或^的理解
- ^ 可理解为不进位相加
- a^a=0
- a^0=a
public static void sway(int[] arr,int i,int j){
if(i!=j){
//不能两个值指向同一地址
arr[i]=arr[i]^arr[j];
arr[j]=arr[i]^arr[j];//就是arr[i]^arr[j]^arr[j]就表示arr[i]
arr[i]=arr[i]^arr[j];//表示arr[i]^arr[j]^arr[i]^arr[j]^arr[j]就是arr[j]
}
}
4.1 寻找数组中出现的单数
4.1.1 题目：一组数只有一个数出现奇数次，其他出现偶数次，找出这个出现奇数次的数
利用 异或的性质
// 只有一种数出现奇数次，其他都出现偶数次
public static int printOddTimesNum1(int[] arr){
int eor = 0;
for(int num : arr){
eor = eor ^ num;
}
return eor; // 如果出现基数次，异或结果就是出现奇数次的数
}- 取出一个数最右边1的位置
int mostRightOne = pos & (~pos + 1);
// mostRightOne值在二进制位上的位次就是pos得最右第一个1的位置
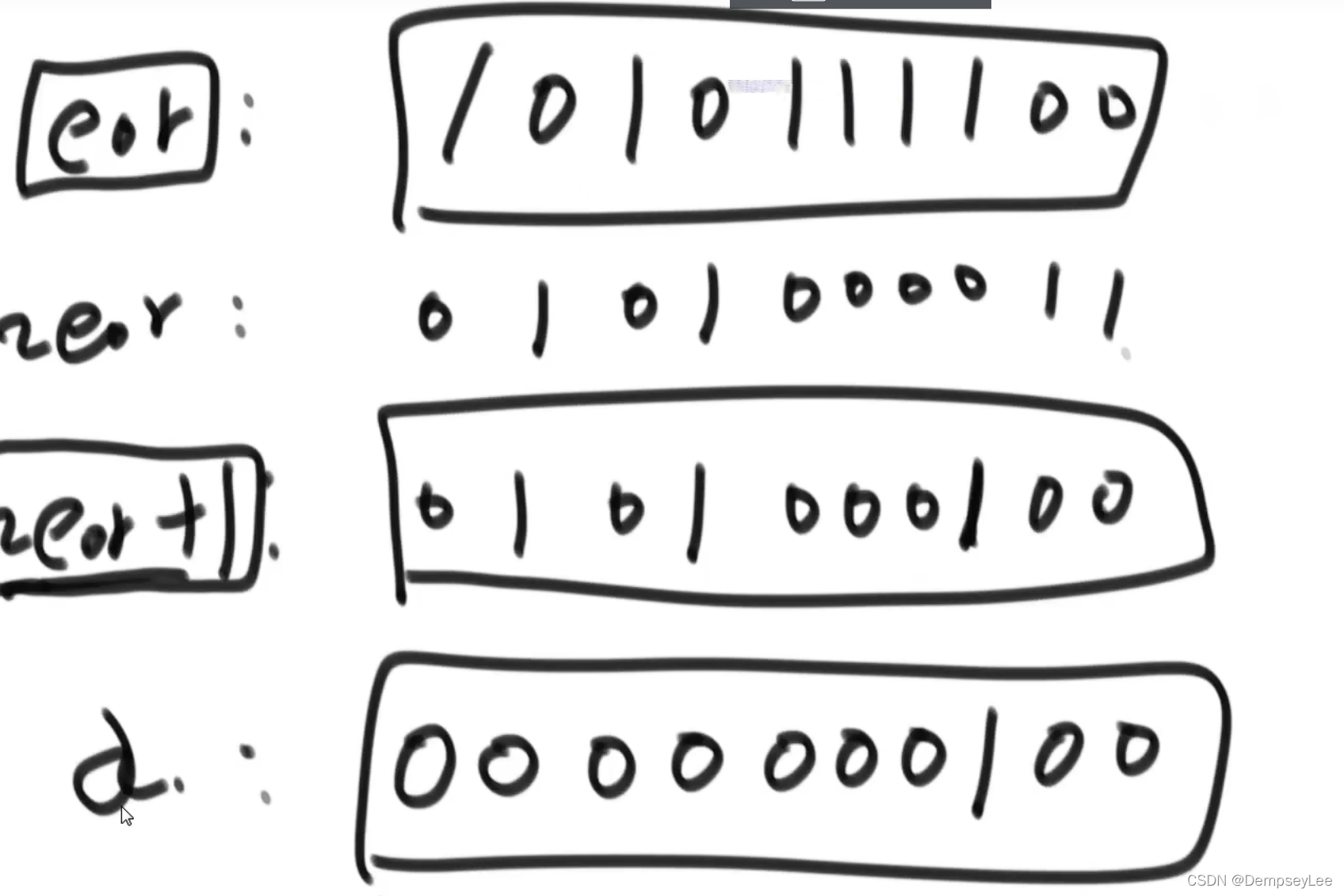
4.1.2 一组数只有两个数出现一次，其他出现两次，找出这两个数：
// 两种数a 和 b出现奇数次，其他数出现偶数次，找这两个数
public static void printOddTimesNum2(int[] arr){
// 先定义一个数对数组中所有数进行异或
int eor = 0;
for(int num : arr){
eor = eor ^ num;
}
//此时 eor = a ^ b;
// eor != 0
// eor 必然有一个位置上等于1
// 下一步是找到 这个位置为1的数，取最右侧1
int rightOne = eor & (~eor + 1); // 取eor最右侧1
// 定义一个eor’ 异或 最右侧1处 为1 的数，可以得到 a 或 b
int onlyOne = 0; // eor‘
for(int num : arr){
if((rightOne & num) == 0) { // 提取数组中右侧不为1的数，这里不能等于1，因为不是二进制数
onlyOne = onlyOne ^ num; // 此时 onlyOne 为啊或 b中的一个数
}
}
System.out.println(onlyOne + " " + (onlyOne ^ eor));
}05 插入排序
插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴，但它的原理应该是最容易理解的了，因为只要打过扑克牌的人都应该能够秒懂。插入排序是一种最简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
插入排序和冒泡排序一样，也有一种优化算法，叫做拆半插入。
5.1 算法步骤
将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）
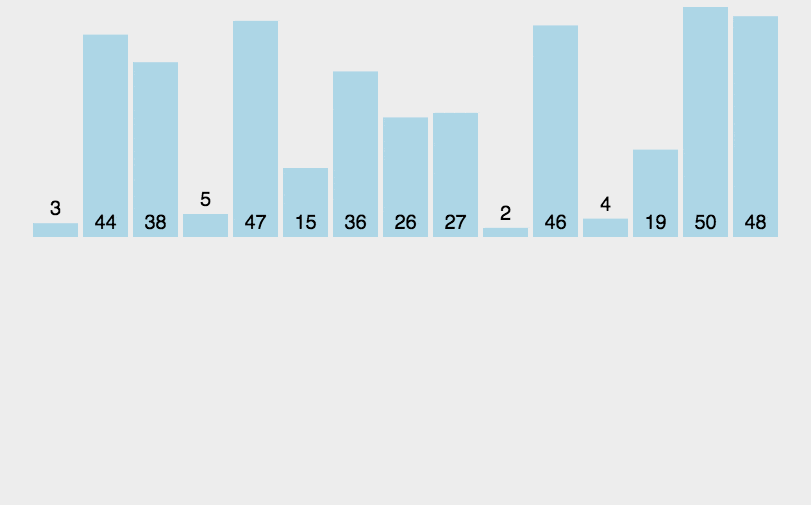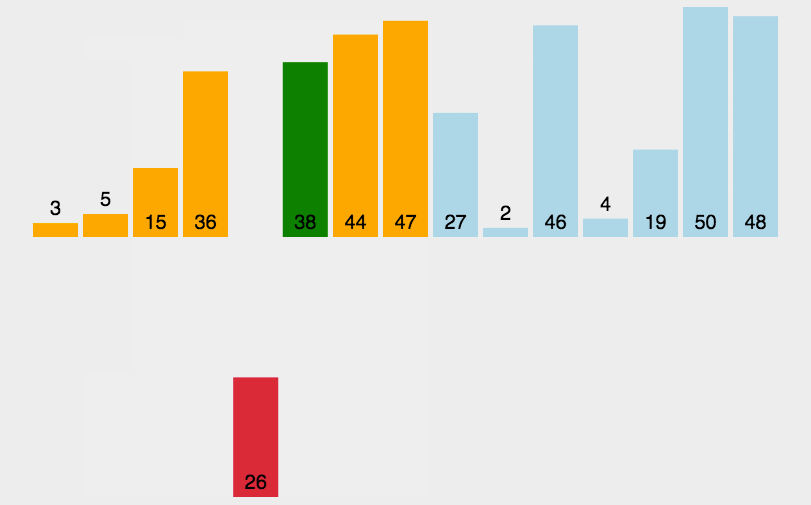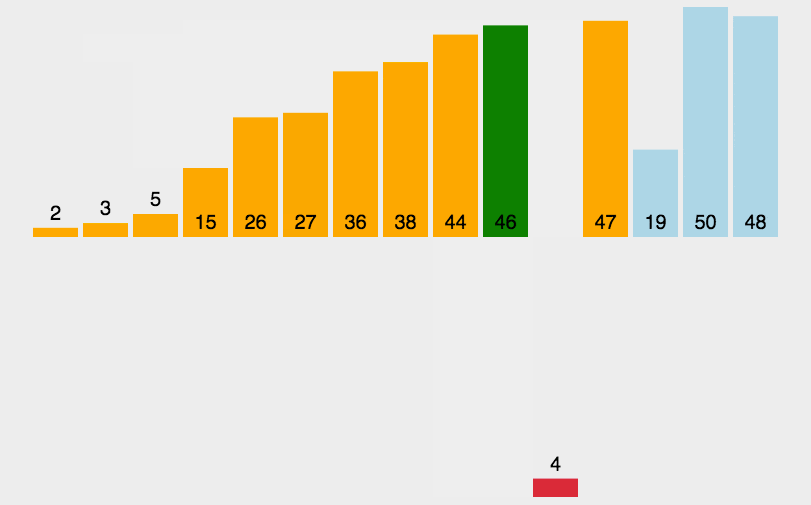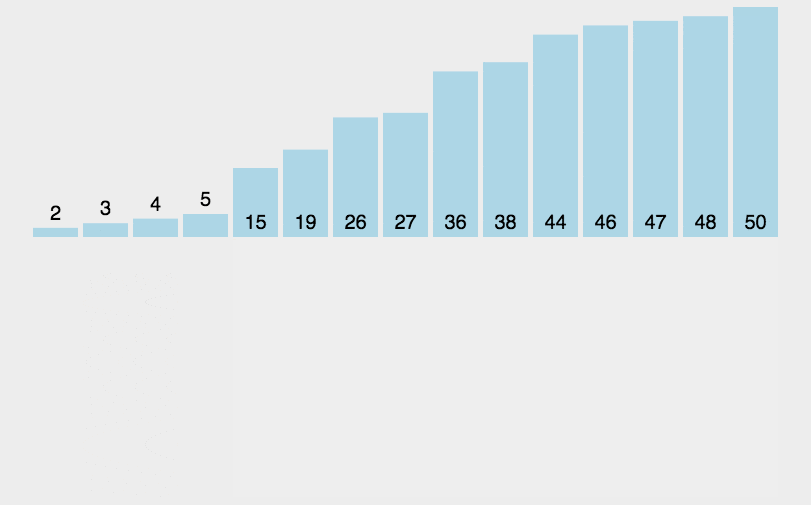
5.2 代码示例
5.2.1 示例1
import java.util.Arrays;
public class InsertionSort {
public static void InsertionSort(int[] arr){
// 首先判断输入合法性
if(arr == null || arr.length < 2){
System.out.println("不需要排序");
return;
}
// 0- 0 有序
// 0 - i 想有序
for(int i = 1; i < arr.length; i++){ //保证0 - i范围有序
for(int j = i; j > 0; j--){ // 新牌为 arr[i], 令arr[i]与前面的数比较
if(arr[j] < arr[j - 1]){
swap(arr,j, j-1);
}
}
}
}
public static void swap(int[] arr, int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args){
int[] arr = new int[]{3,5,2,-2,7,9,-10};
InsertionSort(arr);
System.out.println(Arrays.toString(arr));
}
}5.2.2 示例2
import java.util.Arrays;
public class insertionSort1 {
public static void main(String[] args){
int[] arr = new int[]{3,5,52,-2,7,9,10};
insertSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void insertSort(int[] arr){
if(arr == null || arr.length < 2){
return;
}
int i, j;
for( i = 1; i < arr.length; i++){
int temp = arr[i]; // 取牌
for(j = i ; j > 0 && arr[j - 1] > temp; j-- ){
arr[j] = arr[j - 1]; // 移位
}
arr[j] = temp;
}
}
}5.3 时间复杂度分析
时间复杂度与数据排列情况有关，最好情况： T = O(N)， 最坏情况： T = O（N^2）
06 对数器
使用对数器，具体步骤：
1）有一个你想要测的方法a
2）实现一个绝对正确但是复杂度不好的方法b
3）实现一个随机样本产生器
4）实现比对的方法
5）把方法a和方法b比对很多次来验证方法a是否正确。
6）如果有一个样本使得比对出错，打印样本分析是哪个方法出 错
7）当样本数量很多时比对测试依然正确，可以确定方法a已经 正确。
好处：
验证方法对不对
可以很快找到错误case（几千几万case中）
判断贪心对不对
具体实现（例如测试冒泡排序方法是否正确）：
想要测试冒泡排序方法a（判断该方法是否正确）：
想测的方法a
public static void bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int e = arr.length - 1; e > 0; e--) {//范围每次缩减1，因为每次都排好了一个数
for (int i = 0; i < e; i++) {//从头到e进行两两比较
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1);//（前面比后面大就进行交换）
}
}
}
}
public static void swap(int[] arr, int i, int j) {//两两交换
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
一定正确的方法b： 调用API自带方法一定正确单可能复杂度不好
public static void comparator(int[] arr) {
Arrays.sort(arr);
}
一个随机数据生成器：产生一个长度随机的数组（可能为正，也可能为负，0）
public static int[] generateRandomArray(int maxSize, int maxValue) {
int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
}
return arr;
}
测试
public static void main(String[] args) {
int testTime = 500000;//测试次数
int maxSize = 100;
int maxValue = 100;
boolean succeed = true;
for (int i = 0; i < testTime; i++) {
int[] arr1 = generateRandomArray(maxSize, maxValue);//产生随机数组
int[] arr2 = copyArray(arr1);
bubbleSort(arr1);//测试的方法
comparator(arr2);//绝对正确的方法
if (!isEqual(arr1, arr2)) {
succeed = false;
break;
}
}
System.out.println(succeed ? "Nice!" : "Fucking fucked!");
}
public static boolean isEqual(int[] arr1, int[] arr2) {//实现比对的方法 ，比较两个数组的每个数是否相等
if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
return false;
}
if (arr1 == null && arr2 == null) {
return true;
}
if (arr1.length != arr2.length) {
return false;
}
for (int i = 0; i < arr1.length; i++) {
if (arr1[i] != arr2[i]) {
return false;
}
}
return true;
}
07 二分法详解及扩展（O(Log)）
7.1 在一个有序数组中，找一个数是否存在，复杂度少于（O(N))
public class SearchTest {
public static int search(int[] arr, int num) throws Exception {
int left = 0;
int right = arr.length - 1;
int center;
if(num < arr[left] || num > arr[right] || arr == null){
return -1; // -1表示没有找到
}
while(left <= right){
center = (left + right) / 2 ;// 计算中间元素坐标
if(arr[center] == num){
return center;
}else if(arr[center] < num){
left = center + 1;
}else{
right = center - 1; // 调整右边界
}
}
return -1;
}
public static void main(String[] args){
int[] arr = new int[]{1,2,3,4,5,6,7,8,9,10};
System.out.println(search(arr, 12));
}
}7.2 在一个有序数组中找到 >= 某个数最左侧位置
举例： arr[1,2,2,3,3,4,5,5,5,5,5,5,6,6,6,7]
找到大于等于 5，最左侧位置： 返回 Index = 6
public class SearchTest {
public static int searchLeft(int[] arr, int num) {
int left = 0;
int right = arr.length - 1;
int center = -1;
if (num < arr[left] || num > arr[right] || arr == null) {
return -1; // -1表示没有找到
}
while (left <= right) {
center = (left + right) / 2;// 计算中间元素坐标
if (arr[center] >= num) { // 往左缩小位置
right = center - 1;
} else if (arr[center] < num) { // 往右缩小位置
left = center + 1;
} else {
return center;
}
}
return center;
}
public static void main(String[] args){
int[] arr = new int[]{1,2,2,3,3,4,5,5,5,5,5,5,6,6,6,7};
System.out.println(searchLeft(arr, 5));
}
}7.3 局部最小值问题
给定一个不包含相同元素的整数数组，求一个局部最小值。
题解
1）数组第一个元素比第二个元素小，即为局部最小值。
2）数组最后一个元素比它前一个元素小，即为局部最小值。
3）若不满足，那么局部最小值必可在数组首尾两元素之间的某个位置取得。此时可以采用二分法思想，看中间位置是否符合条件，不符合就分成两部分，从不符合的那一边继续操作。
public class LocalMin {
public static int LocalMinNum(int[] arr){
int left = 0;
int right = arr.length - 1;
int center = -1;
if(arr == null || arr.length <= 1){ // 数组为空或只有一个元素 则返回-1
return -1;
}
if(arr[left] < arr[left + 1]){
return left;
}
if(arr[right] < arr[right - 1]){
return right;
}
// 如果都不满足，则中间移送有一个数满足 arr[i] < arr[i - 1] 且 arr[i] < arr[i + 1]
// 利用二分法
while(left <= right){
center = (left + right) / 2;
if(arr[center] > arr[center - 1]){ // 这种情况向左缩小范围
right = center - 1;
}else if(arr[center] > arr[center + 1] ){ // 向右缩小范围
left = center + 1;
}else{
return center;
}
}
return -1; //中间必然存在一个数满足局部最小值，所以可以直接return center
}
public static void main(String[] args) {
//测试
int[] arr = {10,6,9,50,8,3,20};
System.out.println(LocalMinNum(arr));
}
}
在使用二分法时，要明确向左向右缩小范围的条件！！！
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
