2.18作业

原创于 2024-02-19 00:30:22 发布 · 1k 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #linux #运维

文章讲述了如何使用C语言中的fgets和fopen函数进行文件操作，包括统计文件行数、实现文件之间的拷贝，以及完成简单的注册和登录功能，涉及多路分支选择和文件读写的流程控制。

作业要求：使用fgets统计给定文件的行数

程序代码：

#include<stdlib.h>
#include<string.h>
#include<stdio.h>
 
int main(int argc, const char *argv[])
{
	if(argc!=2)
	{
		printf("input file error\n");
		printf("usage:./a.out filename\n");
		return -1;
	}
	FILE *fp=NULL;
	if((fp=fopen(argv[1],"r"))==NULL)//只读形式打开传入文件
	{
		perror("fopen error");
		return -1;
	}
	char str[50]="";    //搬运字符
	int line=0;  //统计行号
	while(1)
	{
		char *p=fgets(str,sizeof(str),fp);//循环获取文件内每一行字符，并存入str
		if(NULL==p)
		{	
			break;
		}
			line++;
	}
	printf("line=%d\n",line);//循环结束输出行数；
	fclose(fp);
	return 0;
}

运行结果：

作业要求：使用fputs和fgets完成两个文件的拷贝。

程序代码：

#include<stdlib.h>
#include<string.h>
#include<stdio.h>
 
int main(int argc, const char *argv[])
{
	if(argc!=3)
	{
		printf("input file error\n");
		printf("usage:./a.out filename\n");
		return -1;
	}
	FILE *srcfp=NULL; //定义两个文件指针；
	FILE *destfp=NULL; 
    //只读形式打开argv[1]；只写模式打开argv[2]
	if((srcfp=fopen(argv[1],"r"))==NULL || (destfp=fopen(argv[2],"w"))==NULL)
	{
		perror("fopen error");
		return -1;
	}
	char str[50]="";//搬运字符
	while(1)
	{		
		char *p=fgets(str,sizeof(str),srcfp);//将argv[1]中每行字符存入str；
		if(p==NULL)//如果返回NULL；则结束循环
		{
			break;
		}
		fputs(str,destfp);//将每行获取的字符输入到文件argv[2]中；
	}
	return 0;
}

运行结果：

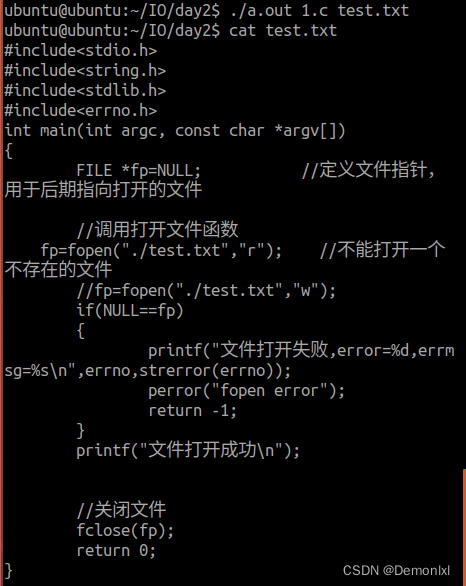
作业要求：

完成注册登录功能

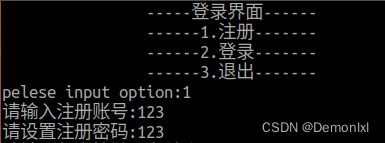
做个小菜单，功能1是注册功能，输入注册账户和注册密码，将账户和密码写入文件中

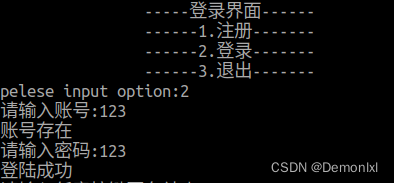
功能2是登录功能，提示并输入登录账户和登录密码，并用其遍历文件中的每一组账户和密码，如果匹配成功，则登录成功，如果全部不匹配则提示登录失败。

程序代码：

#include<stdlib.h>
#include<string.h>
#include<stdio.h>
 
int main(int argc, const char *argv[])
{
	int num=0;
	FILE *fp=NULL;
	char str[50]="";
	while(1)
	{
		system("clear");//执行终端指令
		printf("\t\t-----登录界面------\n");
		printf("\t\t------1.注册-------\n");
		printf("\t\t------2.登录-------\n");
		printf("\t\t------3.退出-------\n");
		printf("pelese input option:");
		scanf("%d",&num);
		getchar();
 
		//对menu进行多分支选择
		switch(num)
		{
		case 1:
			{
				if((fp=fopen("./1.txt","a"))==NULL)
				{
					perror("fopen eerror");
					return -1;
				}
				printf("请输入注册账号:");
				scanf(" %s",str);
				fprintf(fp,"%s\n",str);
				printf("请设置注册密码:");
				scanf(" %s",str);
				fprintf(fp,"%s\n",str);
				fclose(fp);
			}break;
		case 2:
			{
				if((fp=fopen("./1.txt","r"))==NULL)
				{
					perror("fopen eerror");
					return -1;
				}
				char input_str[20]="";
ZHIN:
				printf("请输入账号:");
				scanf(" %s",input_str);
				int flag=0;
				while(1)
				{
					char *p=fgets(str,sizeof(str),fp);
					if(NULL==p)
					{	
						break;
					}
					str[strlen(str)-1]='\0';//结尾添加\0作为字符串标志
					int sub=strcmp(str,input_str); //比较两个字符串
					if(!sub)
					{
						flag++;
						printf("账号存在\n");
						break;
					}
				}
 
				if(0==flag)
				{
					printf("输入的账号不存在\n");
					goto 	ZHIN;
				}
MMIN:
				printf("请输入密码:");
				char input_str1[20]="";
				scanf(" %s",input_str1);	
				while(1)
				{
					char *p=fgets(str,sizeof(str),fp);
					if(NULL==p)
						break;
					str[strlen(str)-1]='\0';
					int sub=strcmp(str,input_str1);
					if(!sub)
					{
						flag++;
						printf("登陆成功\n");
						break;
					}
				}
				if(0==flag)
				{
					printf("输入的密码不正确\n");
					goto 	MMIN;
				}
				fclose(fp);
			}break;
		case 3:goto END;
		default:
			   printf("选择的功能有误,请重新输入\n");
		}
		printf("请输入任意按键回车结束\n");
		while(getchar()!='\n');
	}
END:
	return 0;
}

运行结果：