代码随想录算法训练营第九天|KMP算法、Leetcode28 实现 strStr()、Leetcode459 重复的子字符串

● KMP算法

● KMP算法理论

1.KMP算法与解决问题

KMP算法由三位算法学者：Knuth，Morris和Pratt提出，其名字取三人名字首字母组成。

KMP算法是在文本串txt中查找模式串pattern，如果存在，返回模式串pattern的起始索引，否则返回 -1。

因此KMP算法主要解决的是字符串匹配问题，主要思想是：当出现字符串不匹配时，可以记录部分已经匹配的文本内容，利用这些信息避免从头再进行匹配。

2.最长公共前后缀和前缀表

首先我们需要明确两个概念：
（1）前缀： 不包含最后一个字符的所有以第一个字符开头的连续子串。假如有字符串"abcabcd"，其前缀包括：“a”, “ab”, “abc”, “abca”, “abcab”, “abcabc”;
（2）后缀： 不包含第一个字符的所有以最后一个字符结尾的连续子串。对字符串"abcabcd"其后缀包括：“d”, “cd”, “bcd”, “abcd”, “cabcd”, “bcabcd”。

（1）最长相等前后缀

在这里，我们将最长公共前后缀理解为最长相等/相同前后缀可能会容易搞明白它是什么。
在前缀表中，我们需要记录最长相等/相同前后缀的长度，比方说字符串"aabaa"，其前缀包括"a", "aa", "aab", "aaba", 后缀包括"a", "aa", "baa", "abaa"，其最长相等/相同前后缀就是 aa，因此在前缀表中记录2。

（2）前缀表

前缀表是当出现字符串不匹配时进行回退的，记录了模式串与子串不匹配时，模式串开始重新匹配的位置，即当在某个字符失配时，前缀表会告诉你下一步匹配中，模式串应该跳到哪个位置。
前缀表中记录下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。前缀表要求的就是相同前后缀的长度。

（3）为什么使用前缀表？

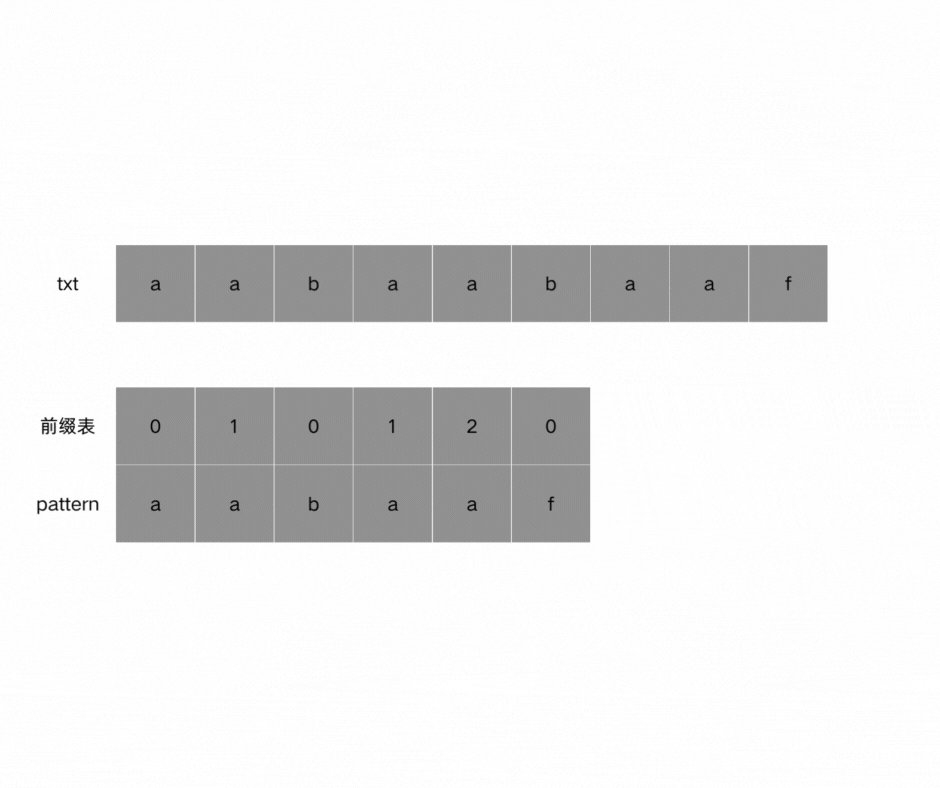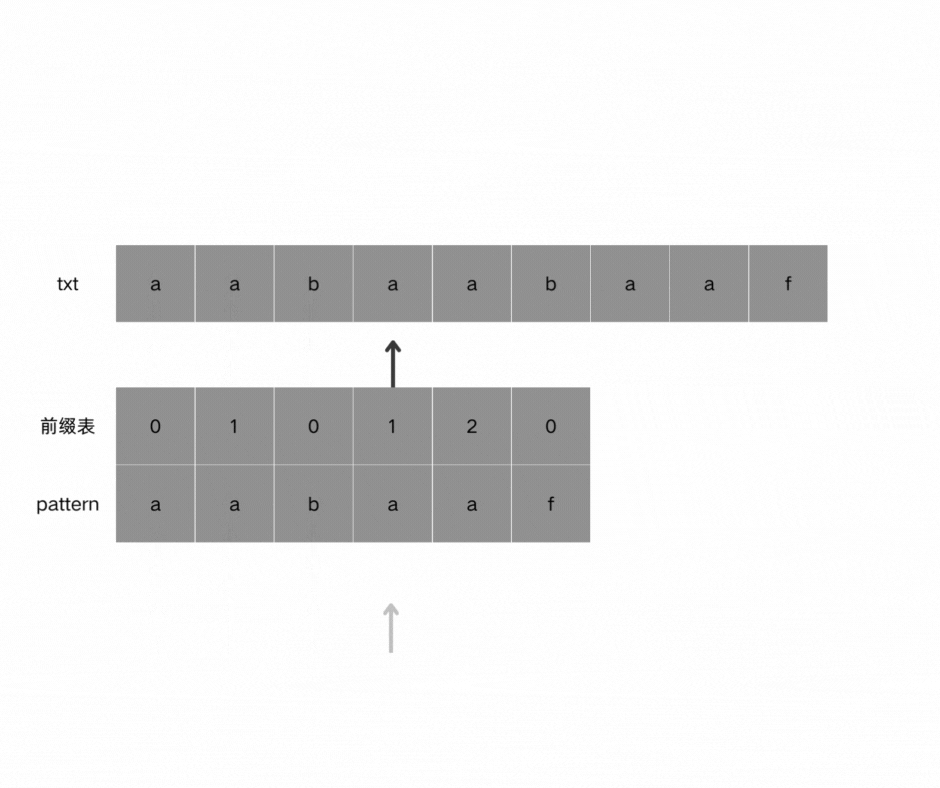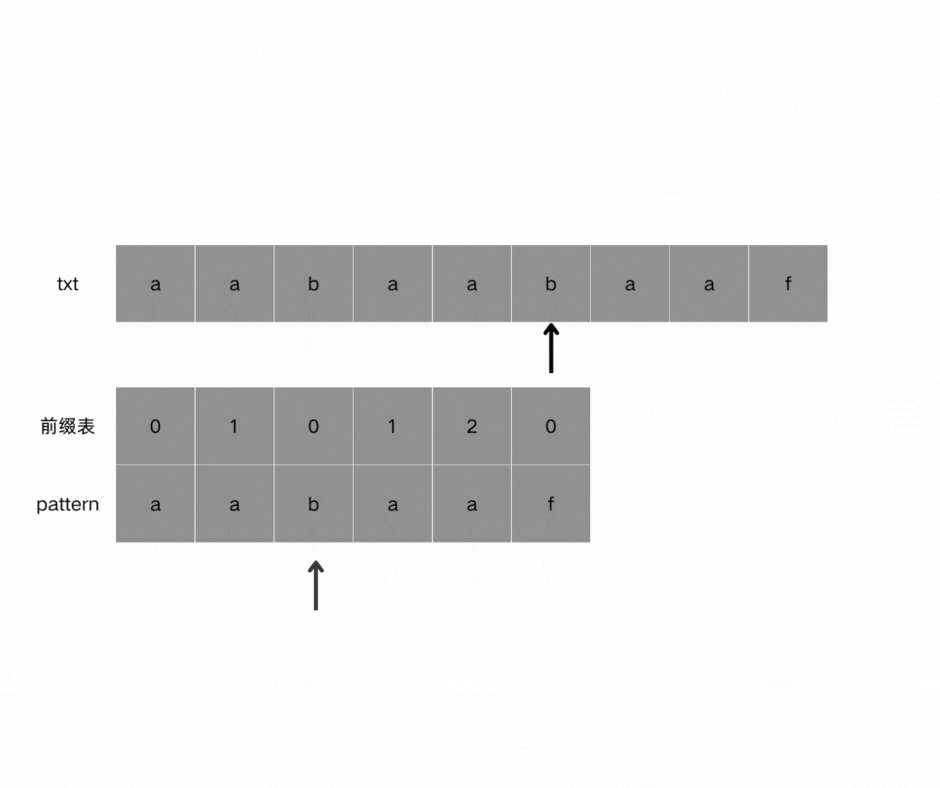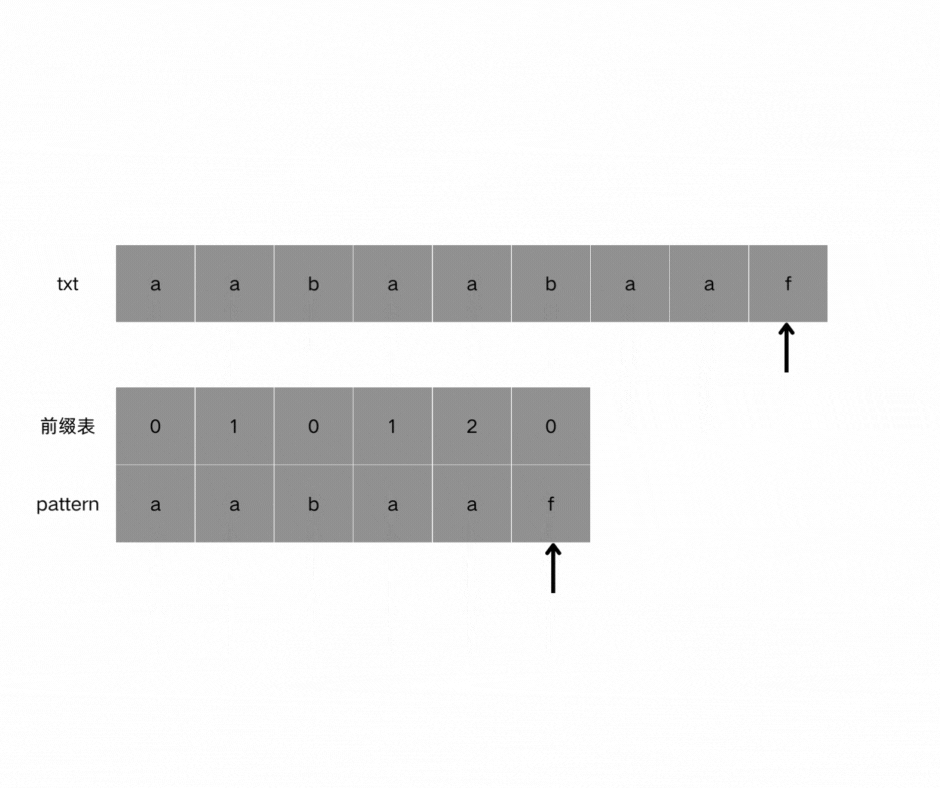
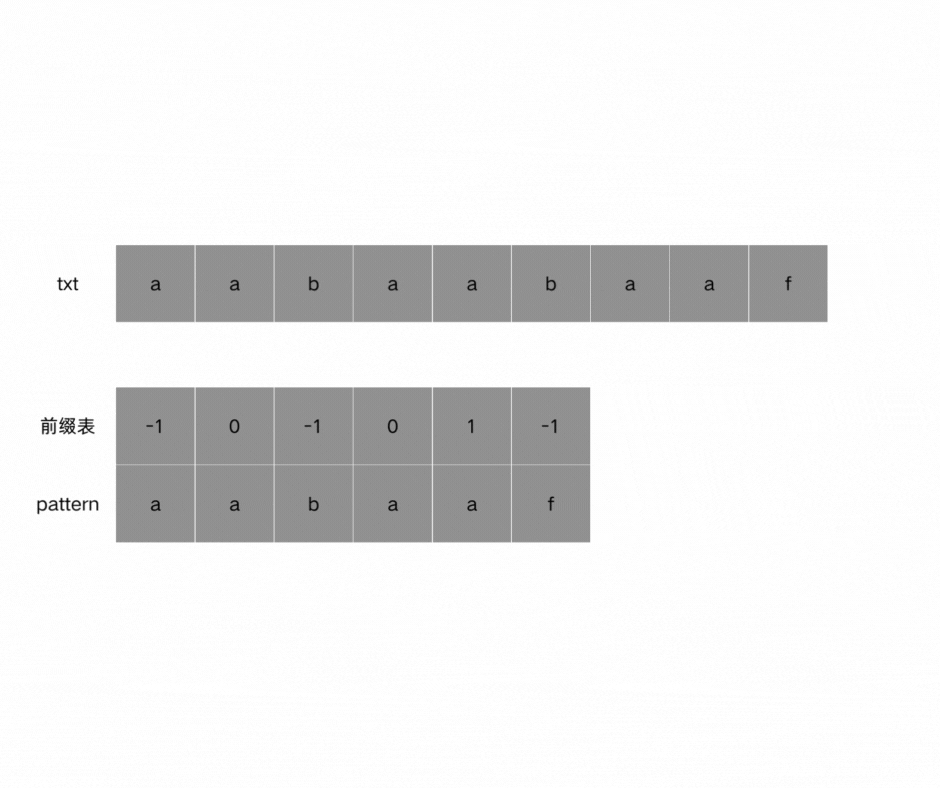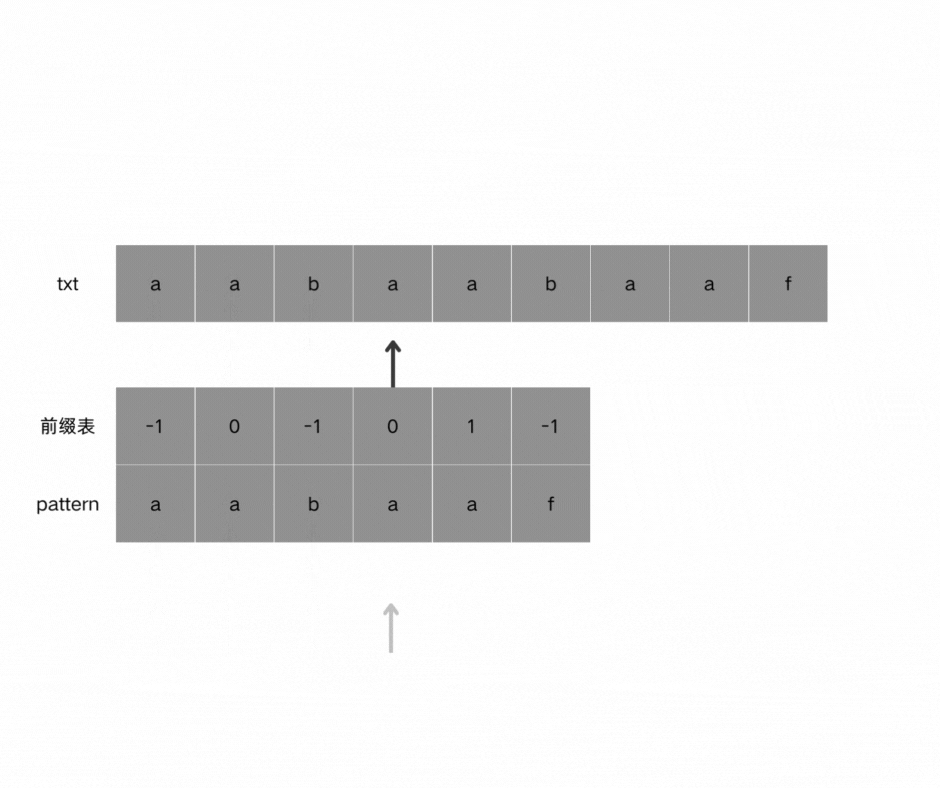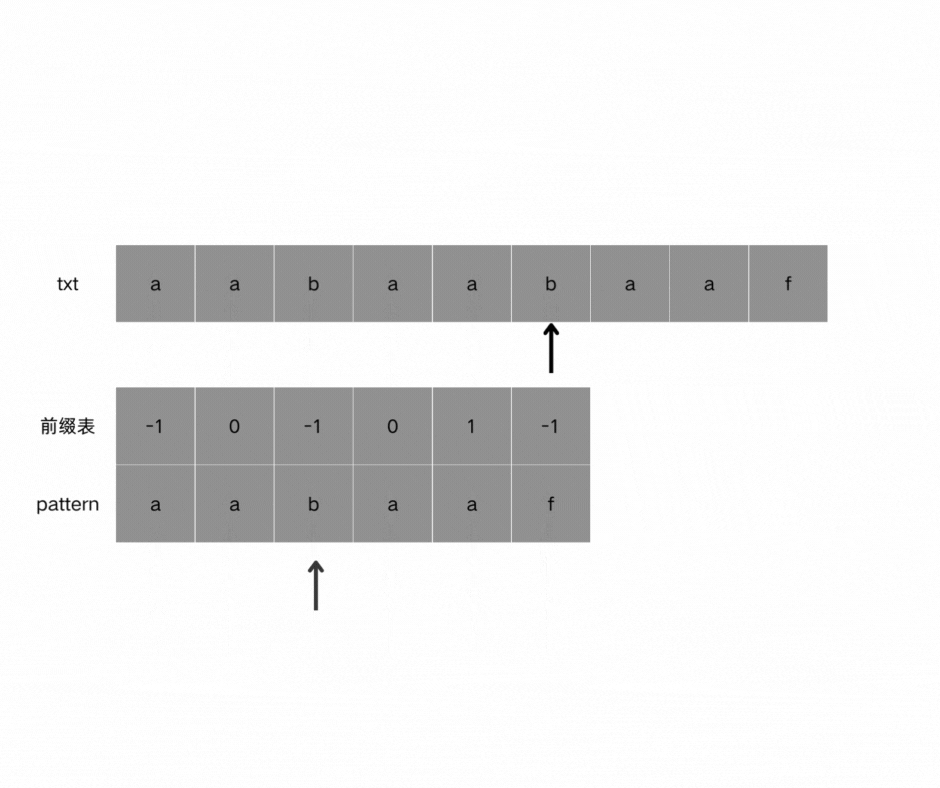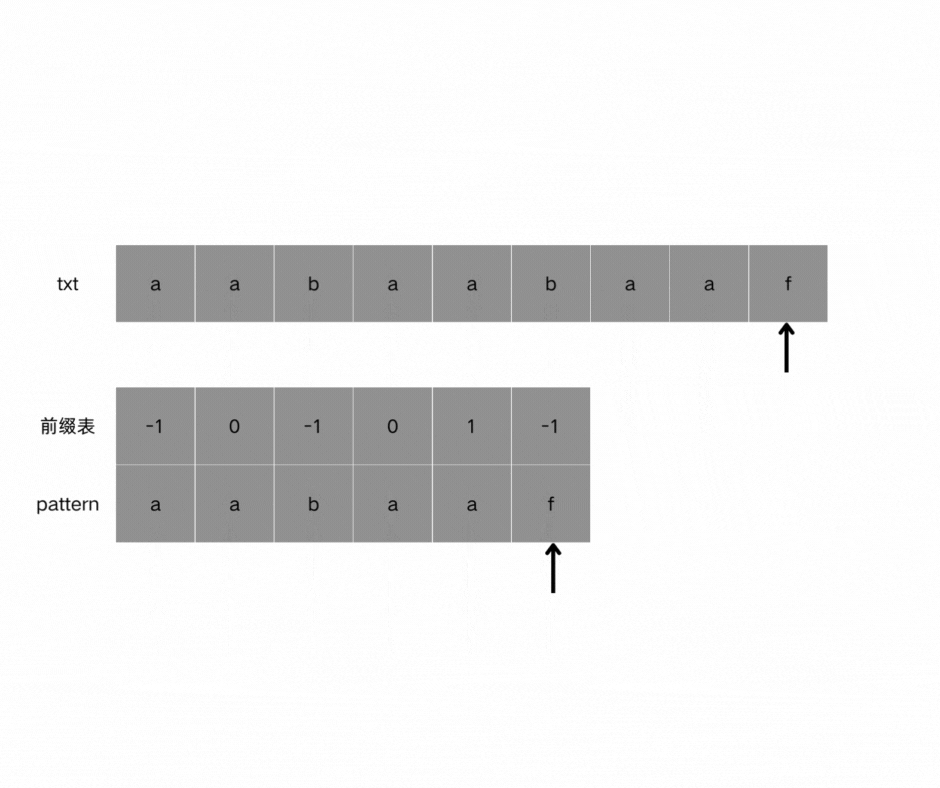
如图，当pattern匹配到f时字符串匹配失败，我们需要看它前一位的前缀表是多少，此时第5个字符记录在前缀表中的记录为2，因此pattern重新指向index == 2，也就是字符b重新进行匹配。因为找到了最长相等的前缀和后缀，匹配失败的位置是后缀子串的后面，那么我们找到与其相同的前缀的后面重新匹配就可以了。

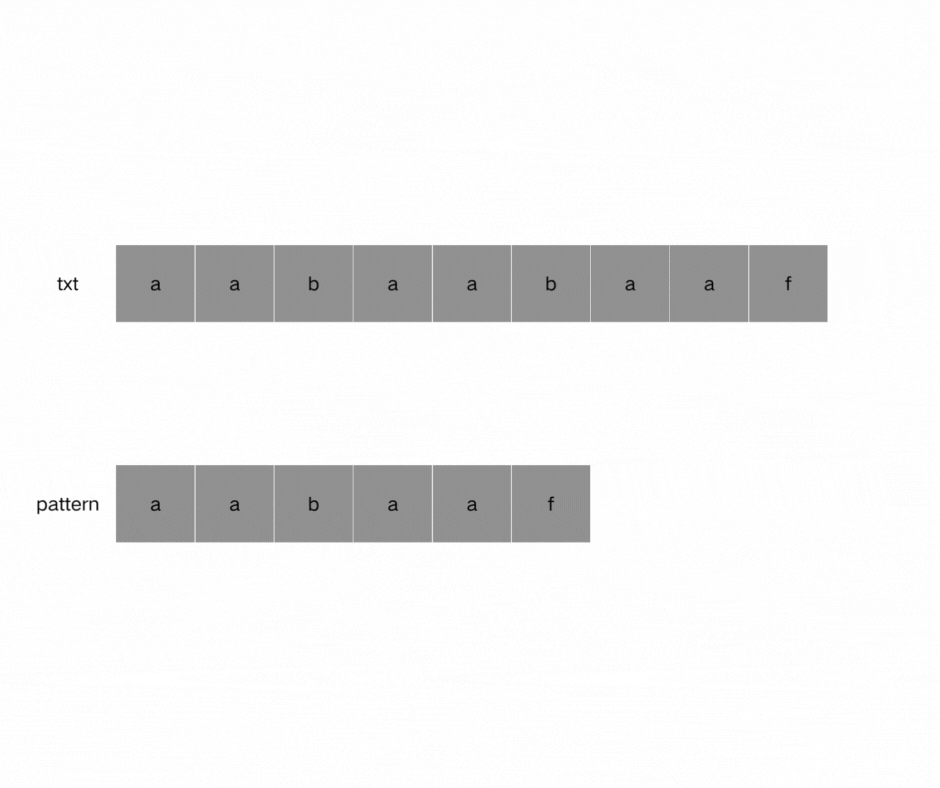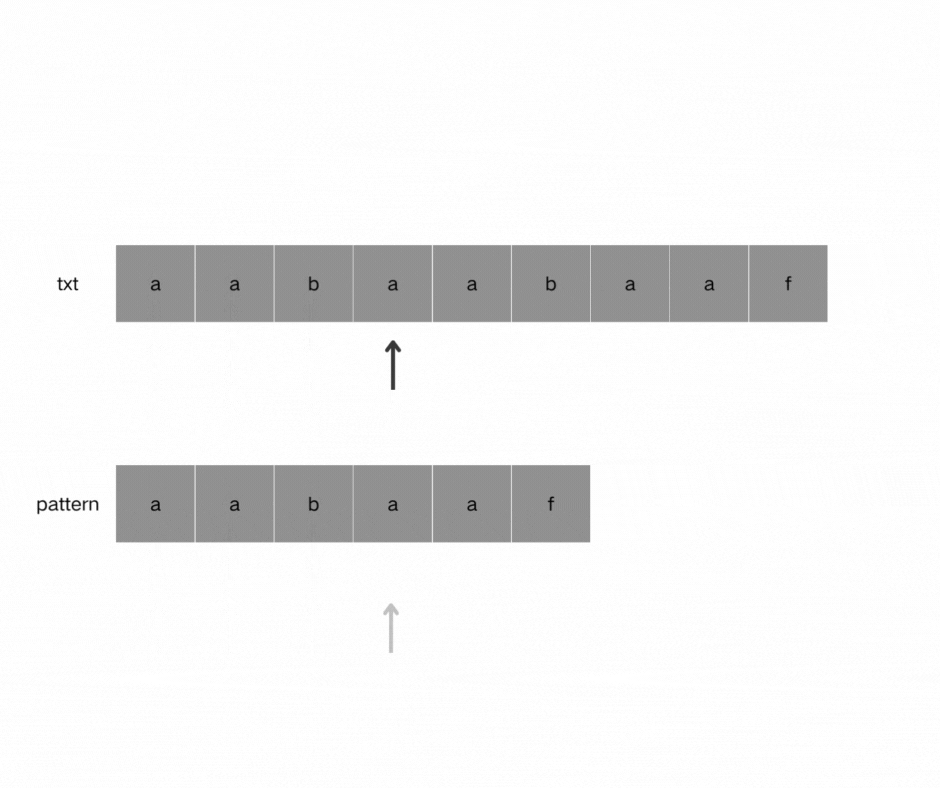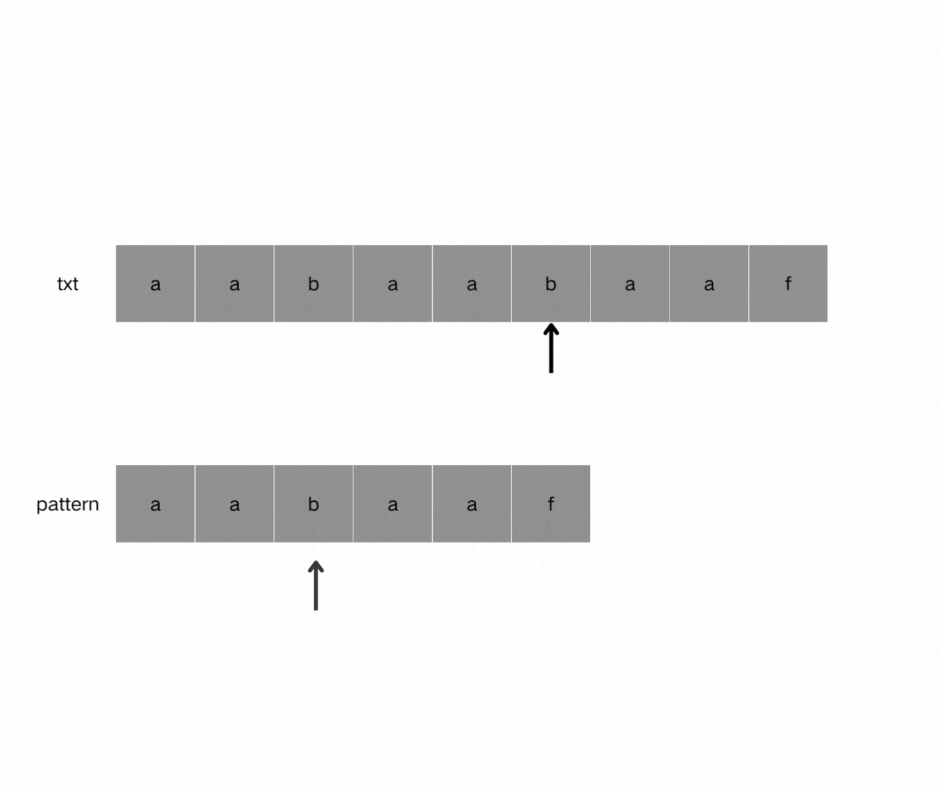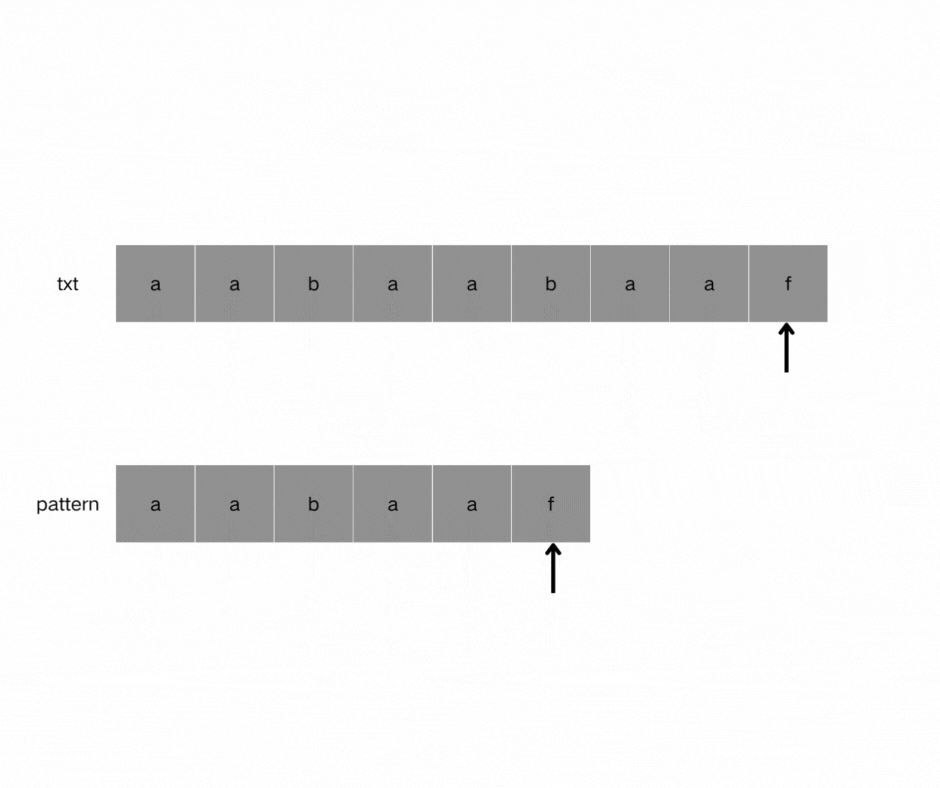
（4）如何计算前缀表

（1）长度为前1个字符的子串a，最长相同前后缀的长度为0；
（2）长度为前2个字符的子串aa，最长相同前后缀的长度为1；
（3）长度为前3个字符的子串aab，最长相同前后缀的长度为0…
以此类推： 长度为前4个字符的子串aaba，最长相同前后缀的长度为1; 长度为前5个字符的子串aabaa，最长相同前后缀的长度为2。 长度为前6个字符的子串aabaaf，最长相同前后缀的长度为0。

那么把求得的最长相同前后缀的长度就是对应前缀表的元素，如图：

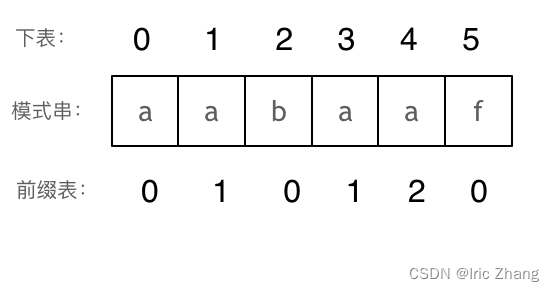
可以看出模式串与前缀表对应位置的数字表示的就是：下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。

如何利用前缀表找到 当字符不匹配的时候应该指针应该移动的位置：

找到的不匹配的位置， 那么此时我们要看它的前一个字符的前缀表的数值是多少。

为什么要前一个字符的前缀表的数值呢，因为要找前面字符串的最长相同的前缀和后缀，所以要看前一位的 前缀表的数值。前一个字符的前缀表的数值是2， 所以把下标移动到下标2的位置继续比配。

最后就在文本串中找到了和模式串匹配的子串了。

（5）前缀表与next数组

next数组就可以是前缀表，有的也成为prefix数组，但是很多实现都是把前缀表统一减一（右移一位，初始位置为-1），之后作为next数组。
不管next采取哪一种形式，与KMP原理都无关，它只关系当发生匹配失败时需要找到那个位置。
（1）前缀表：匹配失败时，回退到前一个字符在前缀表中记录的数值对应的下标处；
（2）前缀表统一减一：匹配失败时，回退到前一个字符在前缀表中记录的数值对应的下标处，只不过需要再重新对其+ 1；
（3）前缀表统一右移一位：匹配失败时，回退到当前字符再前缀表中记录数值对应的下标处。

使用next数组：
定位到Index = 1的下一个元素即可。

3.KMP时间复杂度分析

其中n为文本串长度，m为模式串长度，因为在匹配的过程中，根据前缀表不断调整匹配的位置，可以看出匹配的过程是O(n)，之前还要单独生成next数组，时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。

暴力解法的时间复杂度是O(n × m)，所以KMP在字符串匹配中极大地提高了搜索的效率。

---

● KMP算法实现

next数组构造

定义函数getNext()构造next数组，函数参数为next数组指针以及模式串s：

int getNext(int *next, const string s)

构建next数组的过程就是在计算模式串s前缀表的过程。包含四步：
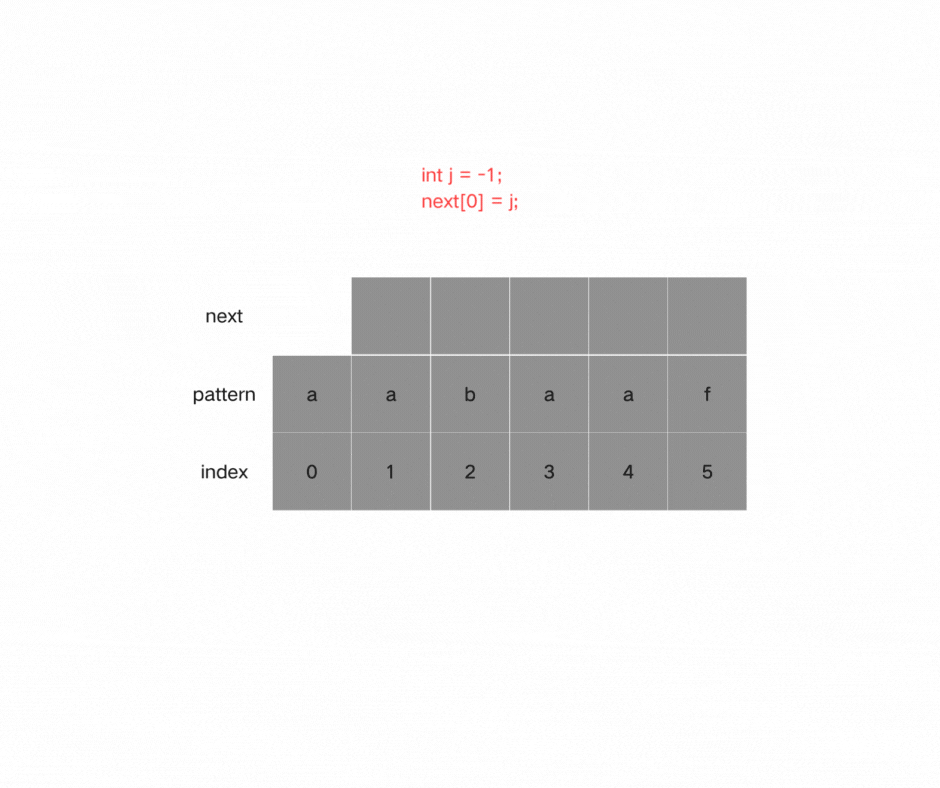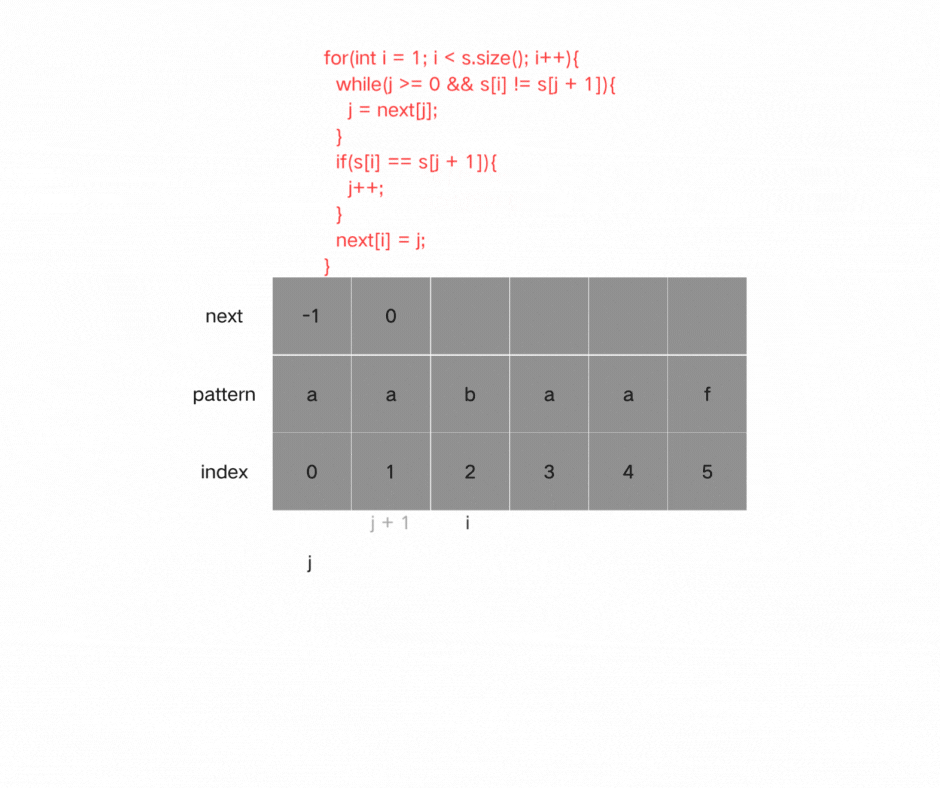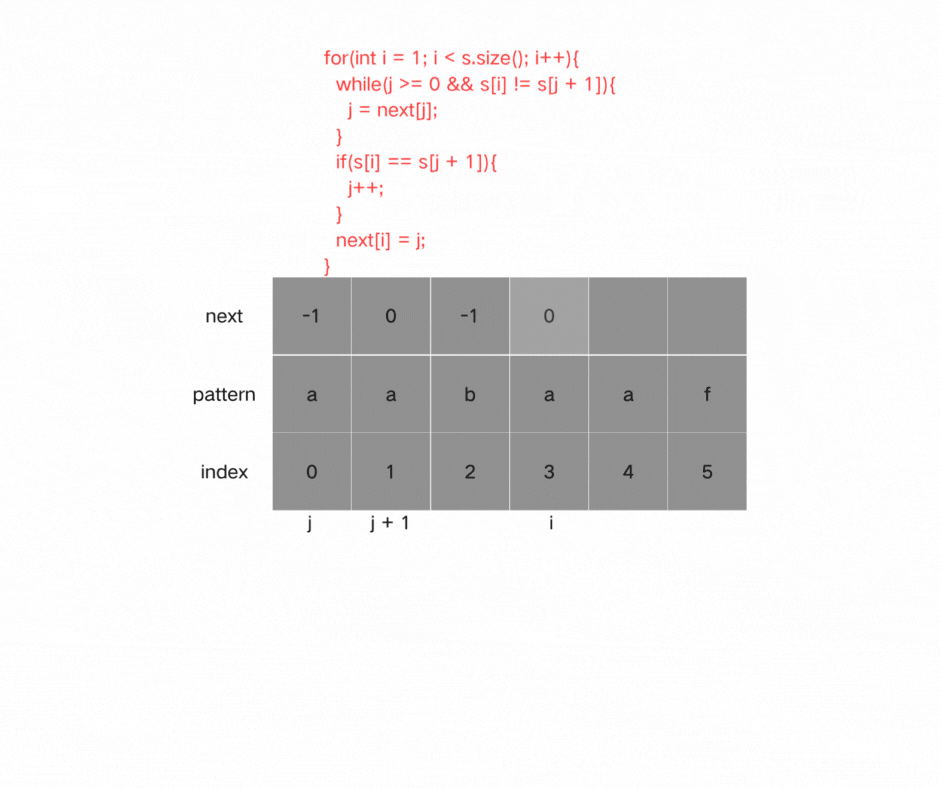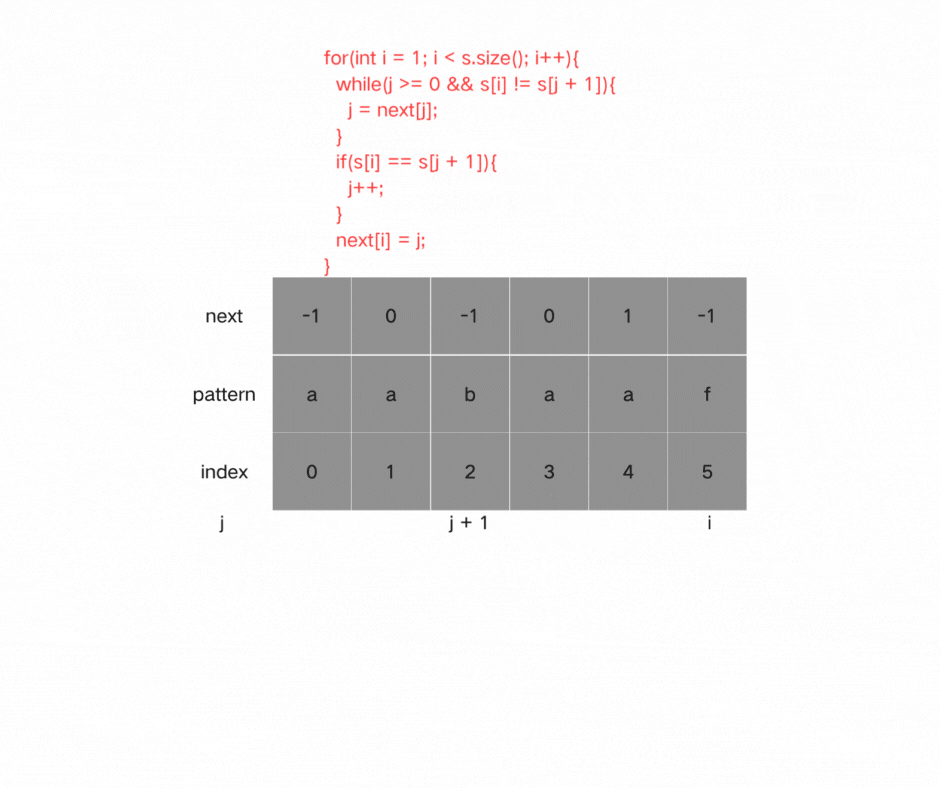
（1）初始化：
定义两个指针i和j，i指向后缀末尾位置，j指向前缀末尾位置，同时j还表示i之前（包括i）子串的最长相等前后缀长度。
对next数组进行初始化：

int j = -1;
next[0] = j;

这里采用前指标统一减一的实现方式，因此j初始化为-1；
next[i] 表示 i（包括i）之前最长相等的前后缀长度（也就是j）。

（2）处理前后缀不相同的情况：
因为j = -1，所以i = 1开始进行比较。
如果s[i] != s[j + 1]，即前后缀末尾不相同时，我们就需要向前回退。next[j]记录j之前字串的相同前后缀长度，因此我们需要找j + 1前一个元素在next数组的值next[j]。

for(int i = 1; i < s.size(); i++)
{
	while(j >= 0 && s[i] != s[j + 1])
	{
		j = next[j];
	}
}

（3）处理前后缀相同的情况：
如果s[i] == s[j + 1]，j向后移动。

if(s[i] == s[j + 1])
{
	j++;
}

（4）更新next[i]：
最后将j（前缀的长度）赋给next[i], 因为next[i]要记录相同前后缀的长度。

next[i] = j;

完整代码如下：

//前缀表统一减一
    int getNext(int *next, const string s)
    {
        int j = -1;
        next[0] = j;
        while(j >= 0 && s[i] != s[j + 1])
        {
            j = next[j];
        }
        if(s[i] == s[j])
        {
            j++;
        }
        next[i] = j;
    }

//前缀表
    void getNext(int* next, const string& s) {
        int j = 0;
        next[0] = 0;
        for(int i = 1; i < s.size(); i++) {
            while (j > 0 && s[i] != s[j]) { // j要保证大于0，因为下面有取j-1作为数组下标的操作
                j = next[j - 1]; // 注意这里，是要找前一位的对应的回退位置了
            }
            if (s[i] == s[j]) {
                j++;
            }
            next[i] = j;
        }
    }

---

● Leetcode28 实现 strStr()

题目链接：Leetcode28 实现 strStr()
视频讲解：代码随想录|实现 strStr()
题目描述：给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回 -1 。

示例 1：
输入：haystack = “sadbutsad”, needle = “sad”
输出：0
解释：“sad” 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ，所以返回 0 。
示例 2：
输入：haystack = “leetcode”, needle = “leeto”
输出：-1
解释：“leeto” 没有在 “leetcode” 中出现，所以返回 -1 。

● 解题思路

利用KMP算法对两个字符串逐一元素进行遍历比较，获得结果。
如果j指向了模式串needle的末尾，那么就说明模式串t完全匹配文本串haystack里的某个子串了。
本题要在文本串字符串中找出模式串出现的第一个位置 (从0开始)，所以返回当前在文本串匹配模式串的位置i 减去 模式串的长度，就是文本串字符串中出现模式串的第一个位置。

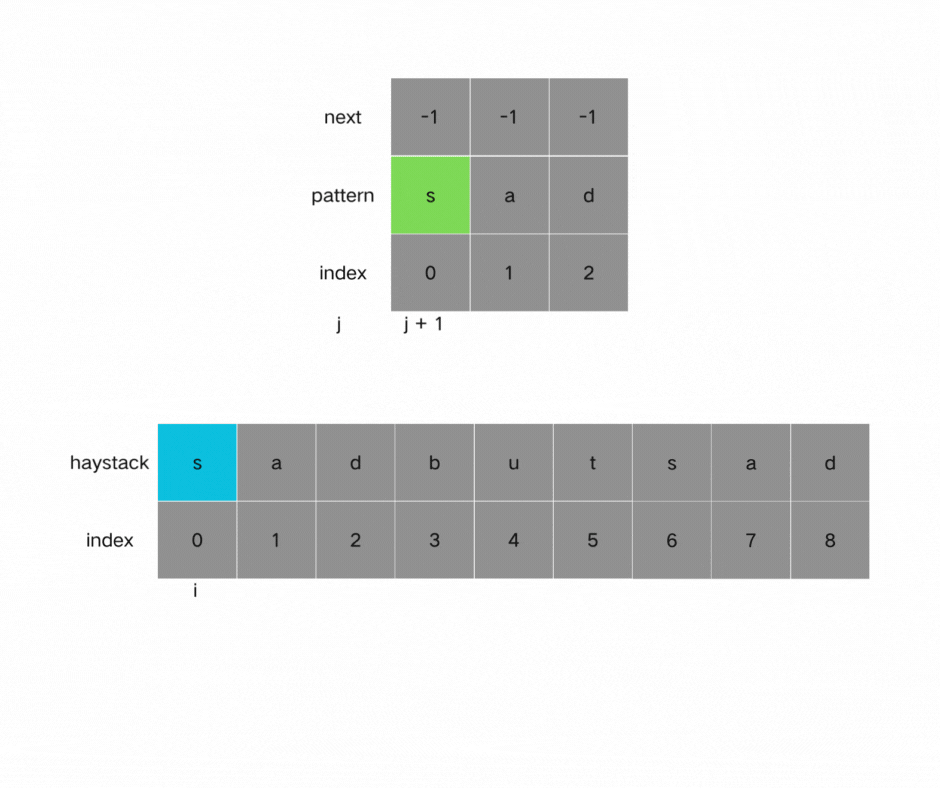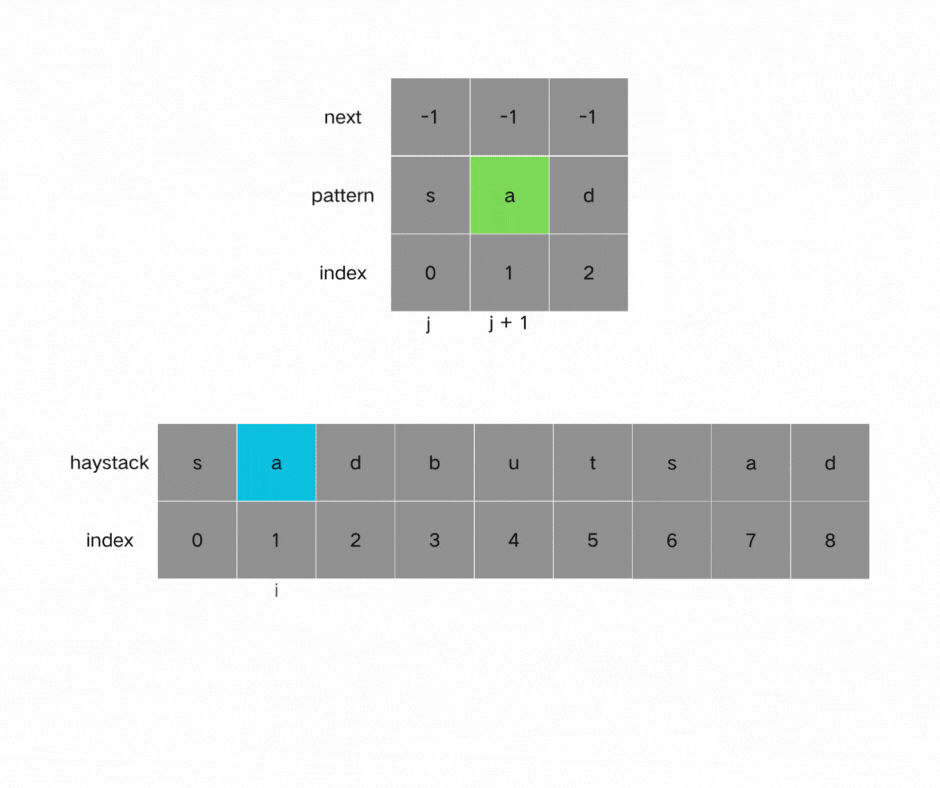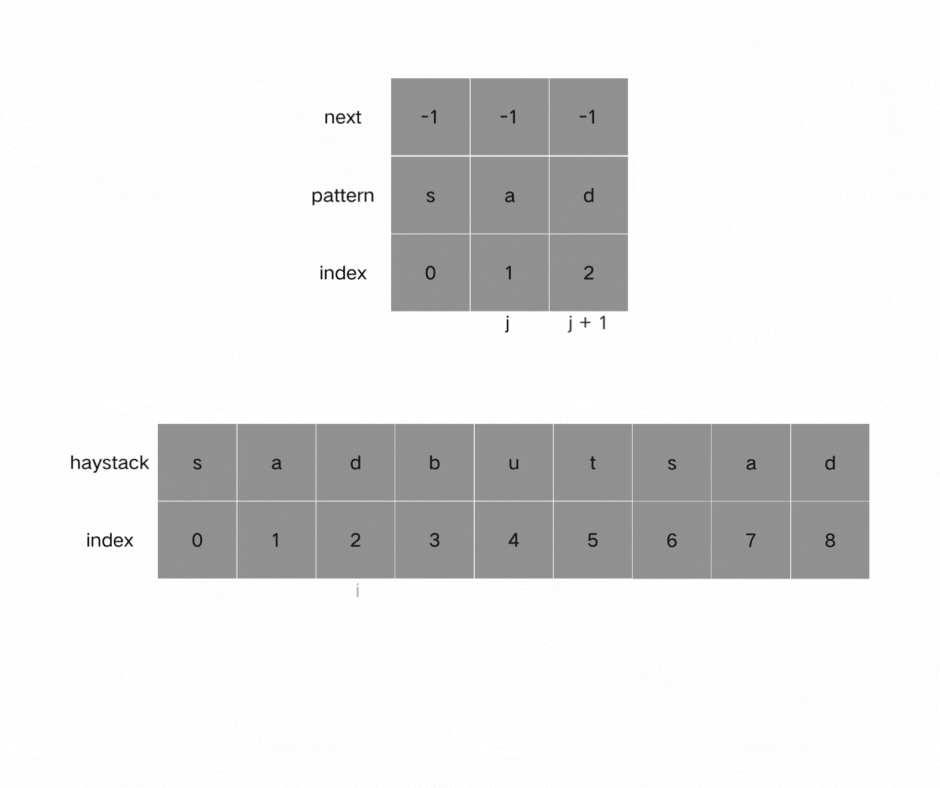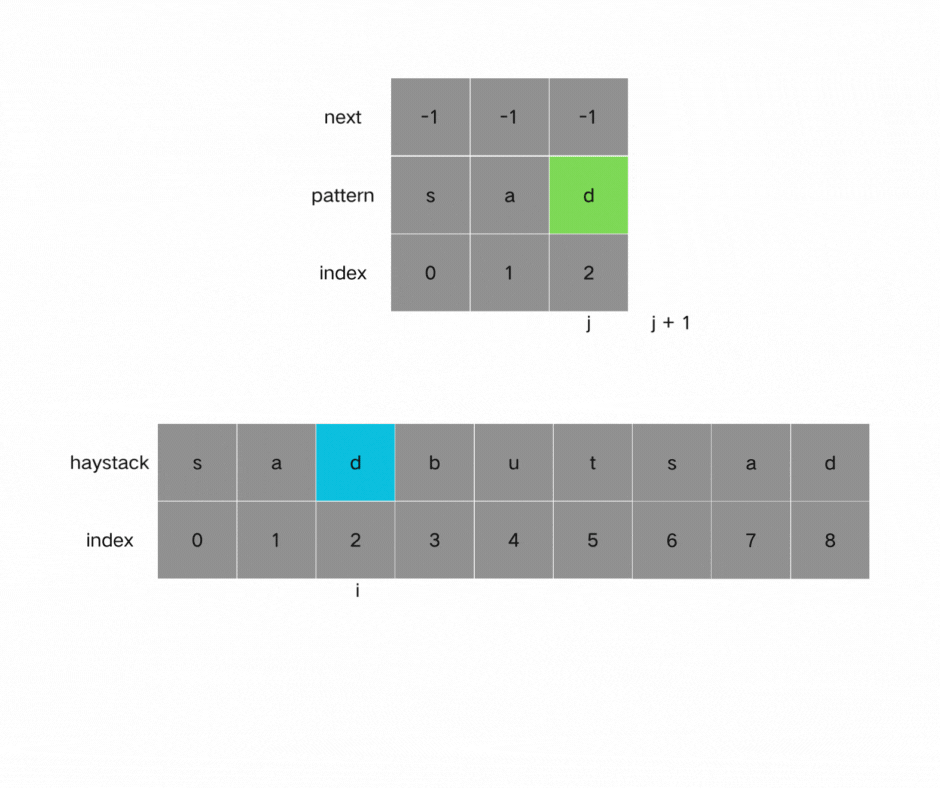
时间复杂度：O(n+m) 空间复杂度：O(m), 只需要保存字符串needle的前缀表
n为haystack的长度，m为needle的长度

● 代码实现

前缀表统一减一

class Solution {
public:
    void getNext(int* next, const string& s)
    {
        //初始化
        int j = -1;
        next[0] = j;

        for(int i = 1; i < s.size(); i++)
        {
            //处理不相等的情况
            while(j >= 0 && s[i] != s[j + 1])
            {
                j = next[j];
            }
            if(s[i] == s[j + 1])
            {
                j++;
            }
            next[i] = j;
        }
    }
    int strStr(string haystack, string needle) {
        if(needle.size() == 0)
        {
            return 0;
        }

        int next[needle.size()];
        getNext(next, needle);

        int j = -1;

        //haystack与needle逐字符对比
        for(int i = 0; i < haystack.size(); i++)
        {
            //不相等情况处理
            while(j >= 0 && haystack[i] != needle[j + 1])
            {
                j = next[j];
            }

            //相等情况处理
            if(haystack[i] == needle[j + 1])
            {
                j++;
            }

            //模式串t完全匹配文本串s里的某个子串了
            if(j == needle.size() - 1)
            {
                return (i - needle.size() + 1);
            }
        }
        return -1;
    }
};

前缀表

class Solution {
public:
    void getNext(int *next, const string& s)
    {
        int j = 0;
        next[0] = 0;

        for(int i = 1; i < s.size(); i++)
        {
            while(j > 0 && s[i] != s[j])
            {
                j = next[j - 1];
            }
            if(s[i] == s[j])
            {
                j++;
            }
            next[i] = j;
        }
    }
    int strStr(string haystack, string needle) {
        if(needle.size() == 0)
        {
            return 0;
        }

        int next[needle.size()];
        getNext(next, needle);

        int j = 0;
        for(int i = 0; i < haystack.size(); i++)
        {
            while(j > 0 && haystack[i] != needle[j])
            {
                j = next[j - 1];
            }
            if(haystack[i] == needle[j])
            {
                j++;
            }
            if(j == needle.size())
            {
                return (i - needle.size() + 1);
            }
        }
        return -1;
    }
};

● Leetcode459 重复的子字符串

题目链接：[Leetcode459 重复的子字符串]
视频讲解：[代码随想录|重复的子字符串]
题目描述：

● 解题思路

方法一：暴力枚举
使用两层for循环，因为最小循环子串必定从s[0]开始，所以第一层for循环遍历循环子串的结束位置，第二层for循环进行比对即可。

时间复杂度：O(n^2) 空间复杂度：O(1)

方法二：移除匹配
因为原字符串由一个最小循环子串循环构成，因此当原字符串+原字符串所构成的新字符串中，必定包含原字符串。但在判断之前需要移出首元素和尾元素，避免因为原字符串位置产生影响。

时间复杂度：O(n) 空间复杂度：O(1)

方法三：KMP算法
通过KMP算法我们可以得到最长相同前后缀，当最长相同前缀 - 最长相同后缀所得即为最小循环子串，得到最小循环子串之后，我们可以通过原字符串总长度对最小循环子串取余必为0从而进行判断。

以下证明最长相同前缀 - 最长相同后缀 = 最小循环子串：
假设最长相同前缀为t，最长相同后缀为k。

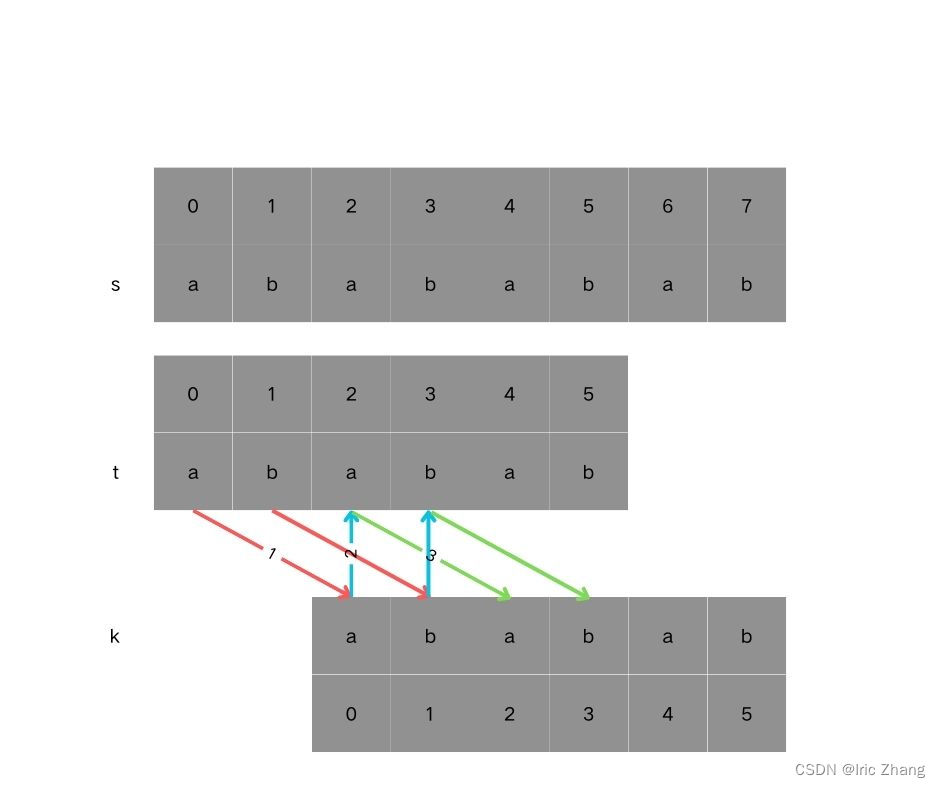
步骤一： 因为 这是相等的前缀和后缀，t[0] 与 k[0]相同， t[1] 与 k[1]相同，所以 s[0] 一定和 s[2]相同，s[1] 一定和 s[3]相同，即：，s[0]s[1]与s[2]s[3]相同 。
步骤二： 因为在同一个字符串位置，所以 t[2] 与 k[0]相同，t[3] 与 k[1]相同。
步骤三： 因为 这是相等的前缀和后缀，t[2] 与 k[2]相同 ，t[3]与k[3] 相同，所以，s[2]一定和s[4]相同，s[3]一定和s[5]相同，即：s[2]s[3] 与 s[4]s[5]相同。
步骤四： 循环往复。

所以字符串s，s[0]s[1]与s[2]s[3]相同， s[2]s[3] 与 s[4]s[5]相同，s[4]s[5] 与 s[6]s[7] 相同。正是因为最长相等前后缀的规则，当一个字符串由重复子串组成的，最长相等前后缀不包含的子串就是最小重复子串。

时间复杂度：O(n) 空间复杂度：O(n)

● 代码实现

方法一：暴力枚举

class Solution {
public:
    bool repeatedSubstringPattern(string s) {
        int n = s.size();
        for (int i = 1; i * 2 <= n; ++i) {
            if (n % i == 0) {
                bool match = true;
                for (int j = i; j < n; ++j) {
                    if (s[j] != s[j - i]) {
                        match = false;
                        break;
                    }
                }
                if (match) {
                    return true;
                }
            }
        }
        return false;
    }
};

方法一：移除匹配

class Solution {
public:
    bool repeatedSubstringPattern(string s) {
        string t = s + s;
        t.erase(t.begin());
        t.erase(t.end() - 1);
        if(t.find(s) != std::string::npos) return true;
        return false;
    }
};

string::npos参数 —— npos 是一个常数，用来表示不存在的位置

方法二：KMP算法

class Solution {
public:
    void getNext(int *next, const string& s)
    {
        int j = 0;
        next[0] = 0;

        for(int i = 1; i < s.size(); i++)
        {
            while(j > 0 && s[i] != s[j])
            {
                j = next[j - 1];
            }
            if(s[i] == s[j])
            {
                j++;
            }
            next[i] = j;
        }
    }
    bool repeatedSubstringPattern(string s) {
        if(s.size() == 0) return false;

        int next[s.size()];
        getNext(next, s);

        int len = s.size();
        if(next[len - 1] != 0 && (len % (len - next[len - 1]) == 0)) return true;
        return false;
    }
};