C语言乘除原理

C语言整数乘除原理

最近在阅读CSAPP时，发现其中讲解乘除原理这一小块内容还蛮有意思的，故自己写一遍帮助理解。

乘以常数

无符号（Unsigned）乘法

由于整数的乘法在机器中的开销相对于加减和移位来说慢得多，因此考虑将乘法转化为加减和移位可以减小开销，提高速度
对于unsigned整数乘以$2^k$的计算来说，就相当于将改整数向左移k位，下面给出证明：
假设该整数的二进制表示为
$$[x_{w-1},x_{w-2},x_{w-3},x_{w-4},\cdots ,x_2,x_1,x_0]$$
则将其转化为十进制的算式为：
$$B2U([x_{w-1},x_{w-2},x_{w-3},x_{w-4},\cdots ,x_2,x_1,x_0])=\sum _{i=0}^{w-1}{x}_i\cdot 2^i$$
将其乘以$2^k$我们可以得到如下推导
$$\begin{array}{r}\sum _{i=0}^{w-1}{x}_i\cdot 2^i\cdot 2^k=\sum _{i=0}^{w-1}{x}_i\cdot 2^{i+k}\end{array}$$
这就相当于将原来的数字左移k位，余位用0补全，用二进制表示为：
$$\begin{array}{rl}& U2B(\sum _{i=0}^{w-1}{x}_i\cdot 2^{i+k})\\ =& [x_{w-1},x_{w-2},x_{w-3},x_{w-4},\cdots ,x_2,x_1,x_0,0_{k-1},0_{k-2},\cdots ,0_2,0_1,0_0]\end{array}$$
由此确定unsigned整数乘以$2^k$等价于其相应二进制数向左移动k位，我们也可以举一个具体的例子来验证：

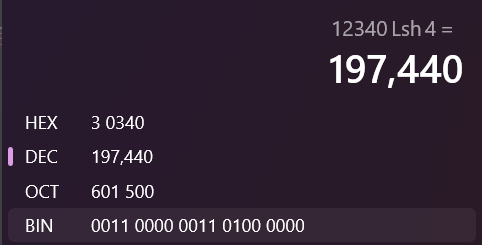
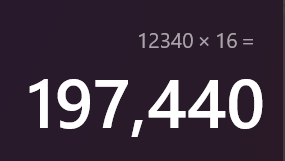
将乘以二的幂次的运算转化为位移运算可以在大部分情况下减小开销，那么如果乘以一个任一的整数呢？
由前面二进制转化为十进制的运算我们可以发现任意一个整数都可以转化为多个二的幂次运算之和，而乘法满足分配律。
因此，我们可以得到以下推导：
$$\begin{array}{rl}& X\cdot Y\\ =& [x_{w-1},x_{w-2},x_{w-3},x_{w-4},\cdots ,x_2,x_1,x_0]\cdot [y_{\lambda -1},y_{\lambda -2},\cdots ,y_0]\\ =& [x_{w-1},x_{w-2},x_{w-3},x_{w-4},\cdots ,x_2,x_1,x_0]\cdot (y_{\lambda -1}\cdot 2^{\lambda }+y_{\lambda -2}\cdot 2^{\lambda -1}+\cdots +y_0\cdot 2^0)\\ =& y_{\lambda -1}\cdot [x_{w-1},x_{w-2},x_{w-3},x_{w-4},\cdots ,x_2,x_1,x_0]\cdot 2^{\lambda }+\\ & y_{\lambda -2}\cdot [x_{w-1},x_{w-2},x_{w-3},x_{w-4},\cdots ,x_2,x_1,x_0]\cdot 2^{\lambda -1}+\\ & \cdots +\\ & y_0\cdot [x_{w-1},x_{w-2},x_{w-3},x_{w-4},\cdots ,x_2,x_1,x_0]\cdot 2^0\end{array}$$
由于y_i只能为0或1这样就可以把整数乘法分解成多个整数位移之和
当然，像14这样的数字，不仅可以转化为$2^3+2^2+2^1$还可以表示为$2^4-2^1$进一步减小运算量
由于无符号乘法的溢出也是通过截断高位来实现的，因此，位移在溢出的情况下得到的结果也相同

补码乘法

对于补码来说，由于无符号乘法和补码乘法的位级等价性，同时溢出也是通过截断高位实现，因此，补码位移也等价于补码的乘法

除以2的幂

在大多数机器上，整数的除法开销还要多余乘法开销，因此除以2的幂时使用移位运算来实现除法也可以减小开销。
但在作除法时，会遇到除不断的情况，此时c语言是如何处理的呢？我们可以先举个例子：

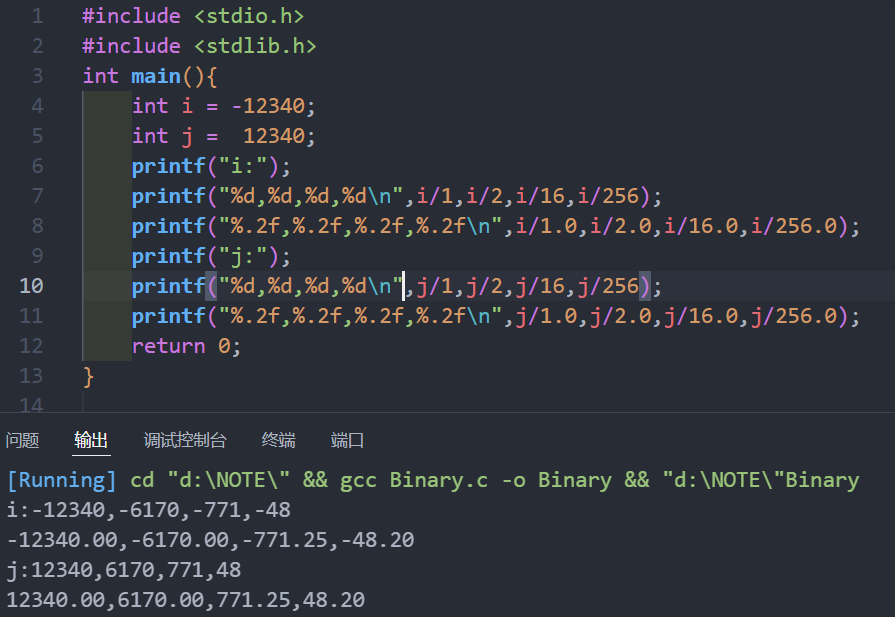
我们可以看到，不论是整数还是负数，c语言的除法都只将小数截断，即对于负数向上取整，对于正数向下取整

无符号除法

对于无符号的数来说，就相当于正数，因此右移就是逻辑右移，得到的结果一定是正确的，推导如下：
计算：$x÷2^k$令,
$$\begin{gathered} x=[x_{w-1},x_{w-2},x_{w-3},x_{w-4},\cdots ,x_2,x_1,x_0] \\ {x}^{\prime }=[x_{w-1},x_{w-2},x_{w-3},x_{w-4},\cdots ,x_k] \\ {x}^{\prime \prime }=[x_{k-1},\cdots ,x_2,x_1,x_0] \end{gathered}$$
则$x=2^k\cdot x^{\prime }+x^{\prime \prime }$,由于$0\le x^{\prime \prime }\le 2^k$因此，$x^{\prime \prime }÷2^k<1$即为小数部分，可以得出$x^{\prime }$就是除法的正确结果，逻辑右移与除法等价

补码除法

对于补码除法，如果是正数则与无符号除法无异，而对于负数，我们可以先举个例子看看：

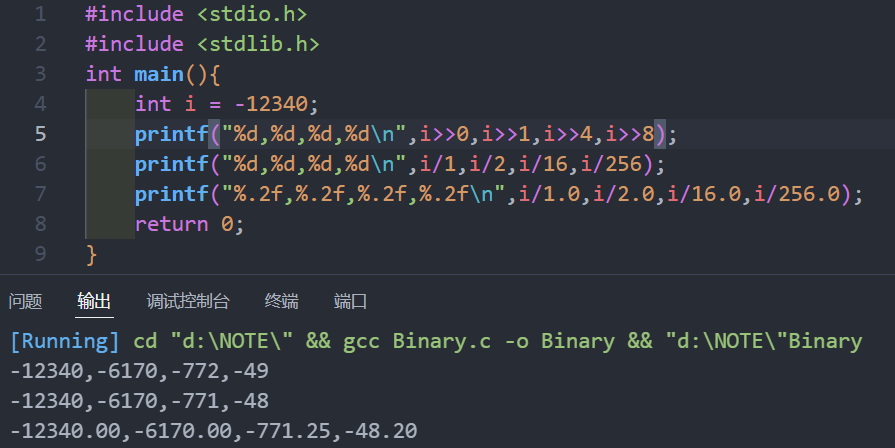
欸？我们发现对于移位来说，负数除法似乎变成像下取整了，这是为什么？
我们可以从数轴上数的关系来看：
对于补码奇数除法与其在数轴上左边相邻偶数除法结果相同。可以举个例子来理解：
对于-7和-8,对应的二进制补码为1111 1001和1111 1000（对于负数补码来说，右移高位补1）可以观察到就末位相差1，而当他们同时除以2时，右移动一位得到相同的结果，如果移动更多位也可以用相似的方式说明，这也就解释了为什么对于负数来说，右移是向下取整。
那么回到C语言中，要实现向零取整应该怎么做呢？
这时候就需要用到偏置技术，如果用$\lfloor \rfloor$表示向下取整，$\lceil \rceil$表示向上取整，则偏执技术的核心是这个公式：
$$\lceil x÷y\rceil =\lfloor (x+y-1)÷y\rfloor (x>y,x,y\in Z,y>0)$$
当x为负数时，我们需要的是$\lceil x÷y\rceil$而仅仅依靠位移能得到的只是$\lfloor x÷y\rfloor$，因此我们需要在做除法之前加上一个偏置$y-1$，令$x=ay+b(0\le b<y)$ :
$$\begin{array}{rl}\lceil (x+y-1)÷y\rceil & =\lfloor (ay+b+y-1)÷y\rfloor \\ & =a+\lfloor (b+y-1)÷y\rfloor \\ & =\{\begin{array}{rlrl}& a+1& & (b\ne 0)\\ & & & \\ & a& & (b=0)\end{array}\\ & =\lceil x÷y\rceil \end{array}$$
至此，我们已经证明加上偏置后作除法就相当于原数向上取整，用在负数的位移上效果也相同。因此，C语言在计算负数二的幂次除法时需要加上偏置
由于除法不满足分配律，因此，除了正二次幂的除法之外，不能使用上述方法，这里也不作其他讨论。