C语言基础9——逻辑结构和存储结构

目录

1、逻辑结构与存储结构

1.1 对比逻辑结构和存储结构

1.2 逻辑结构

1.3 存储结构

1.4 顺序存储与链式存储分析 

2、时间复杂度和空间复杂度

2.1 算法定义

2.2 时间复杂度

2.3 空间复杂度

---

##时间复杂度几乎是每一年大题必考内容！

1、逻辑结构与存储结构

1.1 对比逻辑结构和存储结构

        逻辑结构是数据元素之间的逻辑关系，是抽象的，为人类方便使用，但是想要在计算机中具体实现，就需要数据在计算机中的表示，也就是存储结构。

1.2 逻辑结构

                集合结构：没有特殊关系，共同是一个集合。

                线性结构：一对一的关系。

                树形结构：倒着的树状图。（每个节点，可以有多个孩子，但是只能有一个父亲）

                图形结构：多对多的网状结构。

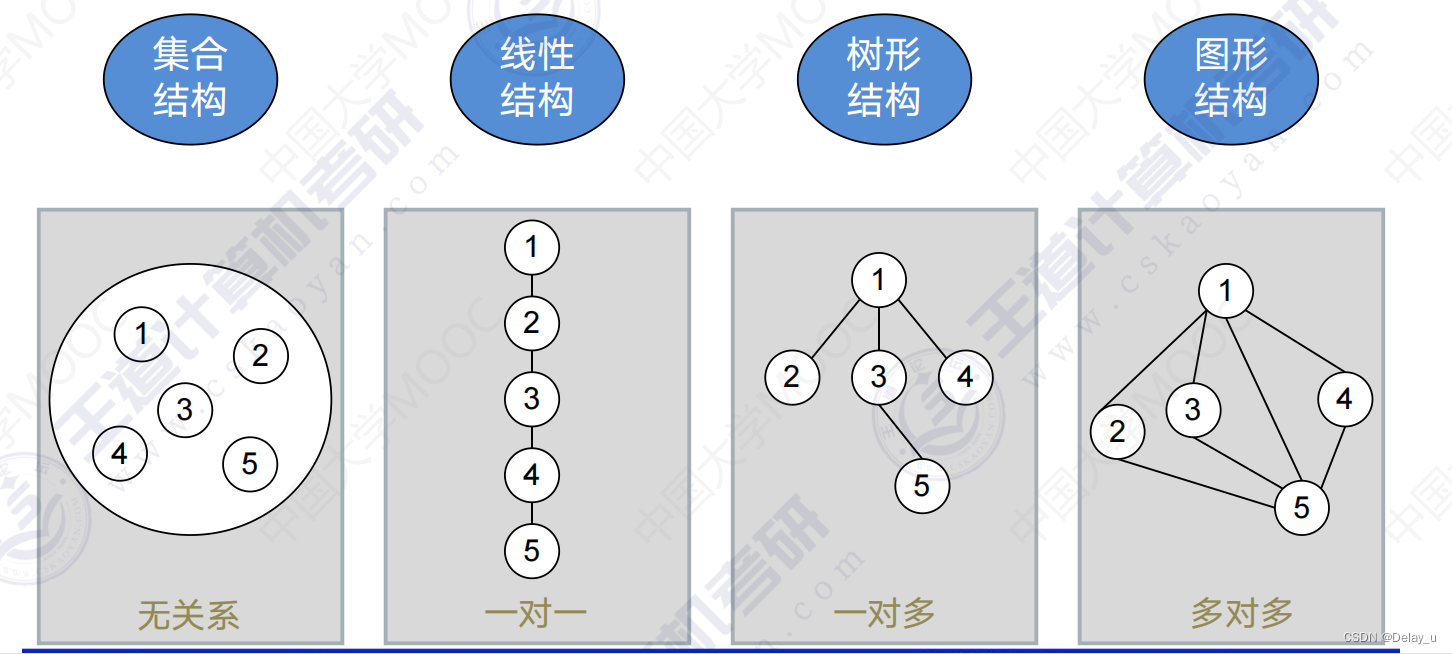
                这么多的逻辑结构如何用计算机代码去实现？

1.3 存储结构

                （就像一枚硬币只有两面一样，元素存储方式也只有挨着或者不挨着两种方式）

                顺序存储：数组就是典型的顺序存储结构，每一个元素都按顺序挨着，

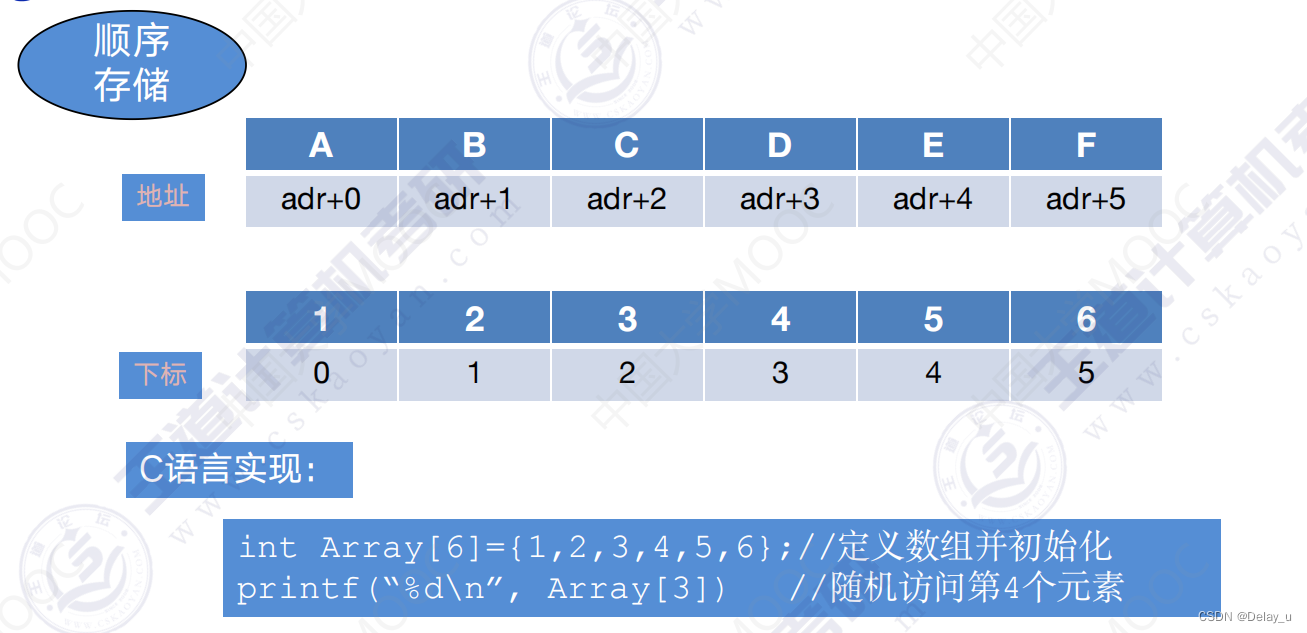（注意：图中随机访问并不是随机访问一个数，而是任意到某一个指定元素，而时间复杂度相同）

                链式存储：假如图中是一个内存段， 就像一列火车的每一个车厢，在车厢的尾部设一个指针指向了下一节车厢。

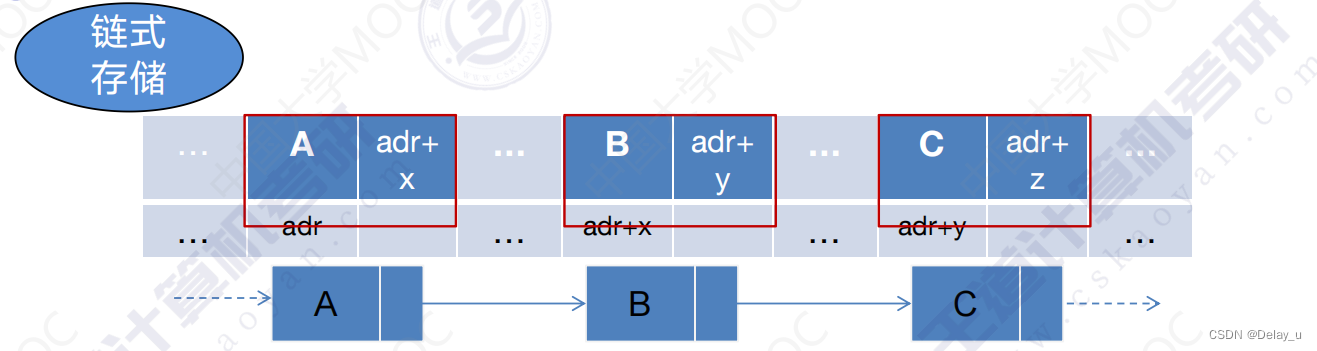
                索引存储，散列存储：（这两种存储依然是根据前两种存储方式完成，可以以后再学）

           总结来说，逻辑结构对人更友好，而存储结构对计算机更友好。而程序员就在解决逻辑结构与存储结构之间的鸿沟。

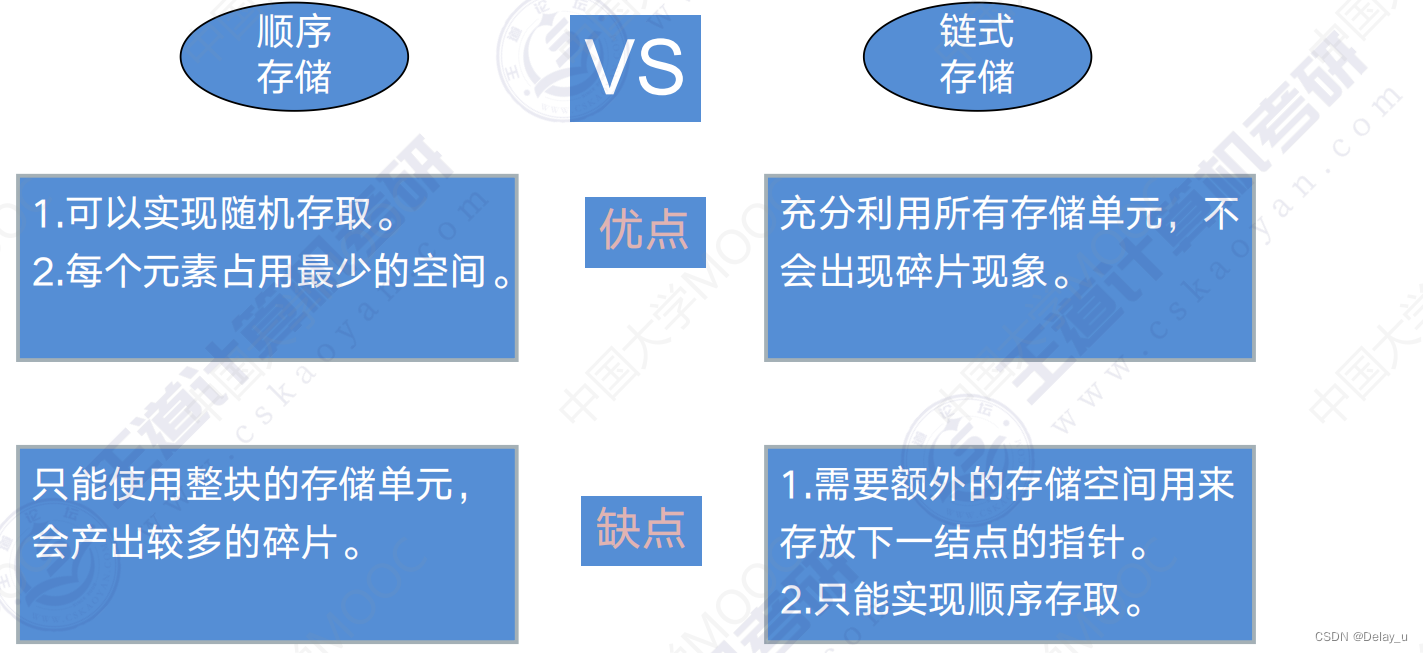
1.4 顺序存储与链式存储分析 

2、时间复杂度和空间复杂度

2.1 算法定义

        在计算时间复杂度和空间复杂度时是去描述某一个算法，例如一个for循环的遍历。

        对特定问题求解步骤的描述，称之为算法，算法的特性有：有穷性、确定性、可行性、输入、输出。

2.2 时间复杂度

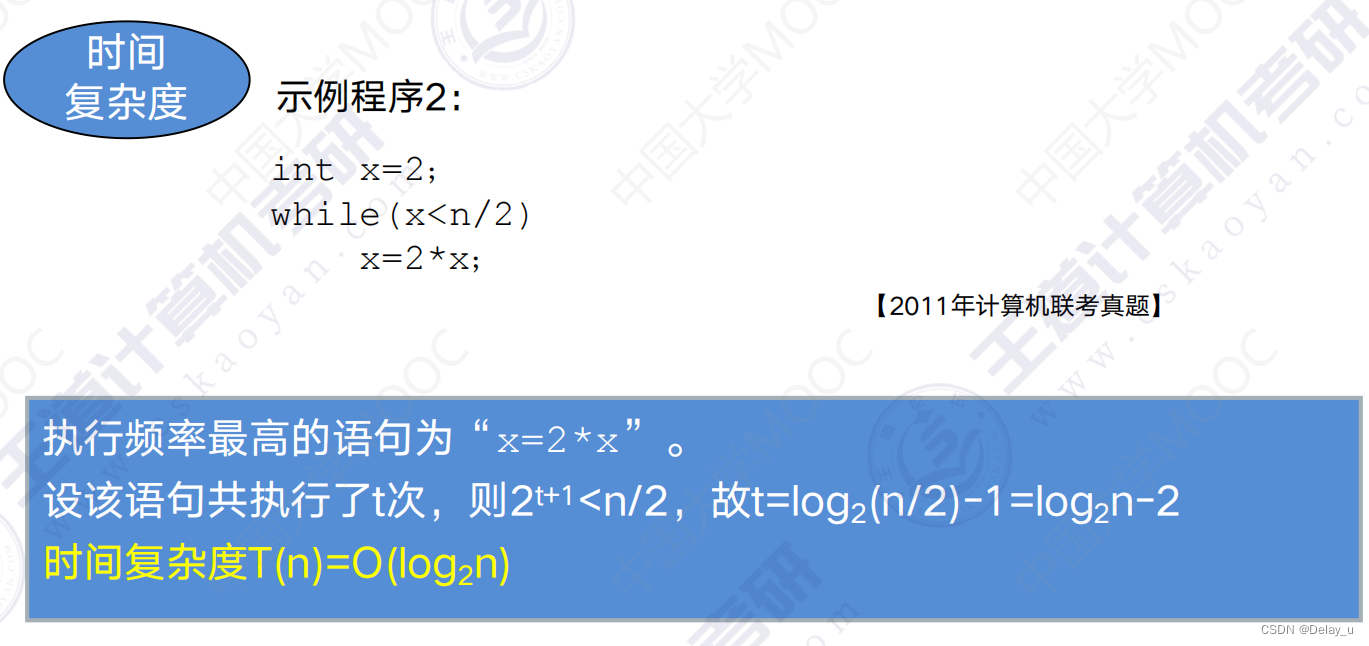
       时间复杂度指算法中所有语句的频度（执行次数）之和。 记为： T(n)=O(f(n))  

       其中，n是问题的规模；f(n)是问题规模n的某个函数。表示随着问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同。

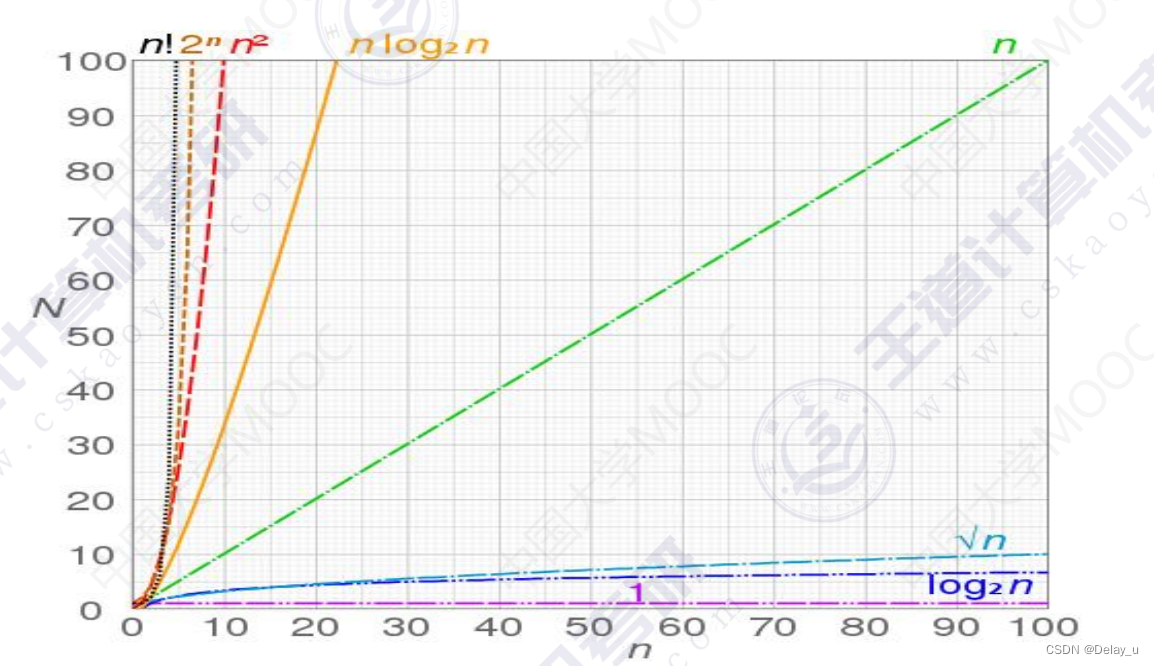
        常见的时间复杂度： Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n^2)＜Ο(n^3)＜Ο(2n) ＜Ο(n!)         最高阶数越小，说明算法的时间性能越好。 

如果一个算法的执行次数 为 3n^3+5n,那么该算法的时间复 杂度为多少？

        D：n^3, 因为时间复杂度的计算会忽略高阶项系数和低阶项。

2.3 空间复杂度

        空间复杂度S(n)指算法运行过程中所使用的辅助空间的大小。 记为： S(n)=O(f(n))

• 除了需要存储算法本身的指令、常数、变量和输入数据外，还需要存储对数据操作的存储单元。
• 若输入数据所占空间只取决于问题本身，和算法无关，这样只需分析 该算法在实现时所需的辅助单元即可。
• 算法原地工作是指算法所需的辅助空间是常量，即O(1)。

        n个元素数组，排序的时候，不使用额外的空间（随着n的增长而增长的空间的叫额外空间），空间复杂度就是O(1)。