动态规划刷题

DeerMer

已于 2022-04-11 15:24:20 修改

阅读量2.2k

点赞数 2

CC 4.0 BY-SA版权

分类专栏：动态规划力扣文章标签： leetcode 算法动态规划

于 2022-03-26 16:24:41 首次发布

本文链接：https://blog.youkuaiyun.com/DeerMer/article/details/123756798

动态规划同时被 2 个专栏收录

1 篇文章

订阅专栏

力扣

1 篇文章

订阅专栏

本文详细解析了多个经典的动态规划问题，包括01背包问题、最长递增子序列、连续子数组最大和等，并提供了清晰的代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

01背包问题

https://www.cnblogs.com/kkbill/p/12081172.html
感觉写的真好！

最长递增子序列（力扣300题）

给定一个整数数组nums，找出其中最长递增子序列的长度

注意：非连续！！！！
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

1、定义状态
dp[i]:以nums[i]为结尾的递增子序列的长度
2、状态转移方程
只要nums[i]严格大于它位置之前的某个数，那么dp[i]=dp[j]+1;
(i是当前数，j是当前数i位置之前的任意一个数，但有可能存在多个大于当前数的数，故dp[i]要实时更新！！)
3、初始化
dp[i]=1;
4、输出
dp数组的最后一个值并不是最长递增子序列的值！！！
dp数组中最大值才是最长递增子序列的值！

public int lengthOfLIS(int[] nums) {
        int[] dp=new int[nums.length];
        //初始化dp数组
        Arrays.fill(dp,1);
        //i表示当前数
        //j表示当前数位置之前的数
        for(int i=1;i<dp.length;i++){
            for(int j=0;j<i;j++){
            //先判断是否符合递增要求
                if(nums[j]<nums[i])
                //若符合递增要求，因可能存在多个符合要求的数，故要实时更新
                dp[i]=Math.max(dp[i],dp[j]+1);
            }
        }
        int max=dp[0];
        //最后遍历dp数组，找到最长递增子序列
        for(int i=1;i<dp.length;i++){
            if(dp[i]>max) max=dp[i];
        }
        return max;
    }

最长子数组和（力扣53题）

给定一个整数数组nums，找出一个具有最大和的连续子数组，返回其最大和
注意：连续子数组！！！
输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

1、定义状态
dp[i]:以nums[i]为结尾的连续子数组的的最大和。
2、状态转移方程
因为要求是连续子数组，且定义的状态时以当前数为结尾的最大和，所以nums[i]一定会被选上。

若dp[i-1]<=0，nums[i]加上他之后，反而变得更小，故dp[i]=nums[i];
若dp[i-1]>0,那么dp[i]=nums[i]+dp[i];

3、初始化
4、输出

public int maxSubArray(int[] nums) {
        int[] dp=new int[nums.length];
        dp[0]=nums[0];
        for(int i=1;i<nums.length;i++){
            if(dp[i-1]>0) dp[i]=dp[i-1]+nums[i];
            else dp[i]=nums[i];
        }
        int max=dp[0];
        for(int i=0;i<dp.length;i++){
            if(dp[i]>max) max=dp[i];
        }
        return max;
    }

打家劫舍（力扣198）

如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你不触动警报装置的情况下，一夜之内能够偷窃到的最高金额。

输入：[1,2,3,1]
输出：4

定义状态
dp[i]：表示前i间房子所能偷盗的最大金额
状态转移方程
假如偷第i间房子，那么dp[i]=dp[i-2]+nums[i-1]
假如不偷第i间房子，那么dp[i]=dp[i-1];
这取决于偷与不偷那个获得的金额最高。

   public int rob(int[] nums) {
        //dp[i]表示 前i间房子所能偷盗的最大金额 
        // 也就解释了 dp数组为啥要申请 n+1的大小
        if(nums.length==0) return 0;
       int n=nums.length;
       int[] dp=new int[n+1];
       dp[0]=0;
       dp[1]=nums[0];
       for(int i=2;i<n+1;i++){
           dp[i]=Math.max(dp[i-2]+nums[i-1],dp[i-1]);
       }
       int max=dp[0];
       for(int i=0;i<n+1;i++){if(max<dp[i]) max=dp[i];}
       return max;
    }

打家劫舍Ⅱ（力扣213）

所有的房屋都围成一圈，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。在不触动警报装置的情况下，今晚能够偷窃到的最高金额。

输入：nums = [2,3,2]
输出：3

和上题类似，只需要分两种情况：

第1间房子~第n-1间房子偷盗的最大金额
第2间房子~第n间房子偷盗的最大金额
取两种情况的最大值即可。
同样 dp[i] 表示前i间房子所能偷盗的最大金额。故dp数组的大小应为n。

 public int rob(int[] nums) {
        int n=nums.length;
        if(n==0) return 0;
        if(n==1) return nums[0];
        //dp[i]前i间房子所能偷盗的最大金额
        int[] dp1=new int[n];
        int[] dp2=new int[n];
        dp1[0]=0;
        dp2[0]=0;
        //dp1表示偷盗第1间到第n-1间
        dp1[1]=nums[0];
        //dp2表示偷盗第2间到第n间
        dp2[1]=nums[1];
        
        //这里的下标比较难搞，手动模拟一下就知道了
        //情况1
        for(int i=2;i<n;i++){
            dp1[i]=Math.max(dp1[i-1],dp1[i-2]+nums[i-1]);
        }

        int max1=dp1[0];
        for(int i=1;i<n;i++){
            if(max1<dp1[i])
            max1=dp1[i];
        }
        //情况2
         for(int i=2;i<n;i++){
            dp2[i]=Math.max(dp2[i-1],dp2[i-2]+nums[i]);
        }
        int max2=dp1[0];
        for(int i=1;i<n;i++){
            if(max2<dp2[i])
            max2=dp2[i];
        }
        return Math.max(max1,max2);
    }

打家劫舍Ⅲ（力扣337）

这个地方的所有房屋的排列类似于一棵二叉树，如果两个直接相连的房子在同一天晚上被打劫，房屋将自动报警。给定二叉树的 root 。返回在不触动警报的情况下，小偷能够盗取的最高金额。

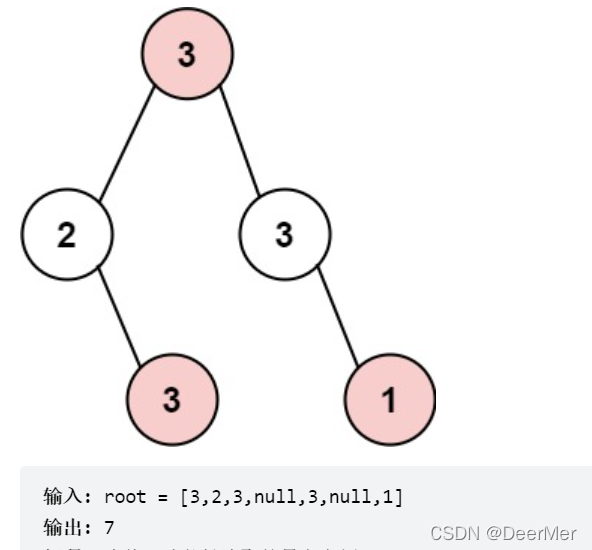
请添加图片描述
首先要明确，这个题需要后序遍历。
思路：一个节点所获得的最大金额取决于两个：

偷这个节点，那么就不能偷这个节点的孩子节点，所以
最大金额=此节点金额+不偷左孩子时，左孩子节点能获得的最大金额+不偷右孩子时，右孩子节点能获得的最大金额
不偷这个节点，那么就可偷可不偷这个节点的孩子节点，所以
最大金额=左孩子能获得的最大金额（可偷可不偷左孩子）+右孩子能获得的最大金额（可偷可不偷右孩子）

最后要注意输出，输出的值是根节点最后的最大值。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
 /**
 1、深度优先遍历（后序遍历）！！
 2、针对一个节点，有两个选择，最后选择root节点的max
  偷此节点所得到的最大值 f(o)，那它的左孩子就不能偷，得到最大值 g(l),右孩子不能偷，得到最大值g(r)
  不偷它所得到的最大值，也就是左孩得到的最大值+右孩得到的最大值 g(o)，左孩右孩可偷可不偷，取决于那个更大？
  */
class Solution {
    //f存放情况1
    Map<TreeNode,Integer> f=new HashMap();
    //g存放情况2
    Map<TreeNode,Integer> g=new HashMap();
    public int rob(TreeNode root) {
        dfs(root);
        return Math.max(f.getOrDefault(root,0),g.getOrDefault(root,0));
    }
    public void dfs(TreeNode root){
        if(root==null) return;
        dfs(root.left);
        dfs(root.right);
        f.put(root,root.val+g.getOrDefault(root.left,0)+g.getOrDefault(root.right,0));
        g.put(root,Math.max(f.getOrDefault(root.left,0),g.getOrDefault(root.left,0))+Math.max(f.getOrDefault(root.right,0),g.getOrDefault(root.right,0)));
    }
}

跳跃游戏（力扣55）

给定一个非负整数数组 nums ，你最初位于数组的第一个下标。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

思路：每次在上次能跳的范围内选一个能跳的最远的位置。

 public boolean canJump(int[] nums) {
        int k=0;
        for(int i=0;i<=k;i++){
        //k实时刷新
            k=Math.max(i+nums[i],k);
            if(k>=nums.length-1) return true;
        }
        return false;

    }

跳跃游戏Ⅱ（力扣45题）

思路：每次在上次能跳的范围内选一个能跳的最远的位置

    public int jump(int[] nums) {
       //思路：每次在上次能跳的范围内选一个能跳的最大的范围
       int max=0;//目前能跳到的最远位置
       int end=0;//上一跳能跳到的最远位置
       int step=0;

       for(int i=0;i<nums.length-1;i++){
       //注意：这里的最后一步到length-1
           max=Math.max(max,i+nums[i]);
           if(i==end){
               end=max;
               step++;
           }
       }
       return step;
    }

买卖股票的最佳时机（力扣121）

 public int maxProfit(int[] prices) {
        //动态规划思想 dp[i]表示第i天的最小值（也就是0~i的最小值） dp[i]=min(dp[i-1],price[i]);
        //只是这里只用到了dp[i-1],故优化为min
        //第i天的最大收益就是 price[i]-dp[i]
        int minprice=prices[0];
        int maxprice=0;
        for(int i=0;i<prices.length;i++){
            if(prices[i]<minprice){
                minprice=prices[i];
            }else{
                if(prices[i]-minprice>maxprice){
                    maxprice=prices[i]-minprice;
                }
            }
        }
        return maxprice;

    }