1046 Shortest Distance (20分)

最新推荐文章于 2024-12-13 11:01:16 发布

原创最新推荐文章于 2024-12-13 11:01:16 发布 · 379 阅读

0 ·

CC 4.0 BY-SA版权

PTA 专栏收录该内容

41 篇文章

订阅专栏

本文探讨了一种计算环形路径上两点间最短距离的算法，通过两次尝试优化解决方案，最终采用预计算节点到起点距离和环总长的方法，实现高效查询。代码示例使用C++编写。

题目描述

原题链接
在这里插入图片描述

思路分析

这个题的意思是求一个环中两点之间的最短距离，当时，第一想法就是先顺着来一圈，再逆着来一圈，最后取这两的最小值就行了。可是……w(ﾟДﾟ)w
在这里插入图片描述

#include <iostream>
using namespace std;
int arr[100010];
int main()
{
	ios::sync_with_stdio(false);
	int n;
	cin >> n;
	for (int i = 1; i <= n; ++i)
	{
		cin >> arr[i];
	}
	int m;
	cin >> m;
	for (int i = 1; i <= m; ++i)
	{
		int a, b;
		cin >> a >> b;
		if (a>b)
		{
			int tmp = a;
			a = b;
			b = tmp;
		}
		int sum1 = 0;
		for (int j = a; j < b; ++j)
		{
			sum1 += arr[j];
		}
		// cout << sum1 << endl;
		int sum2 = 0;
		for (int j = b; ; ++j)
		{
			if (j > n)
			{
				j = 1;
			}
			if (j==a)
			{
				break;
			}
			sum2 += arr[j];
		}
		// cout << sum2 << endl;
		cout << min(sum1, sum2) << endl;
	}
	return 0;
}

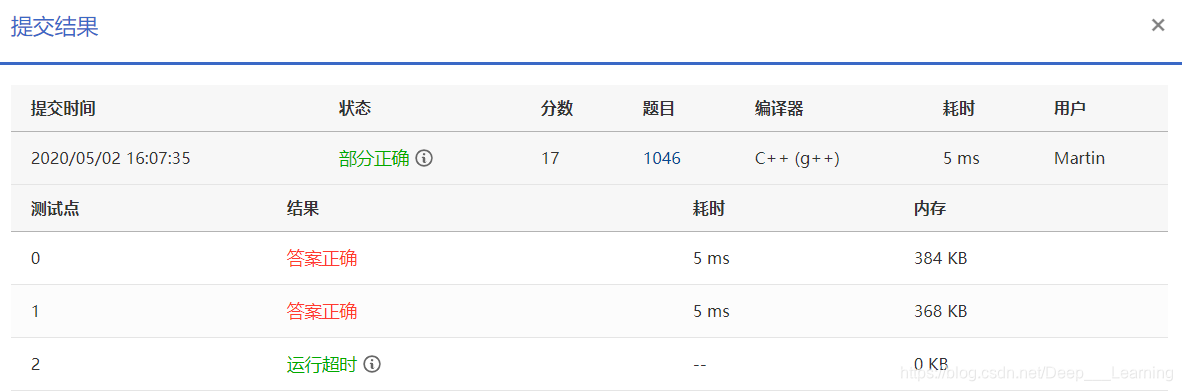
在这里插入图片描述

在这里插入图片描述
最后一个点超时了，木得办法，只能再换一个思路。
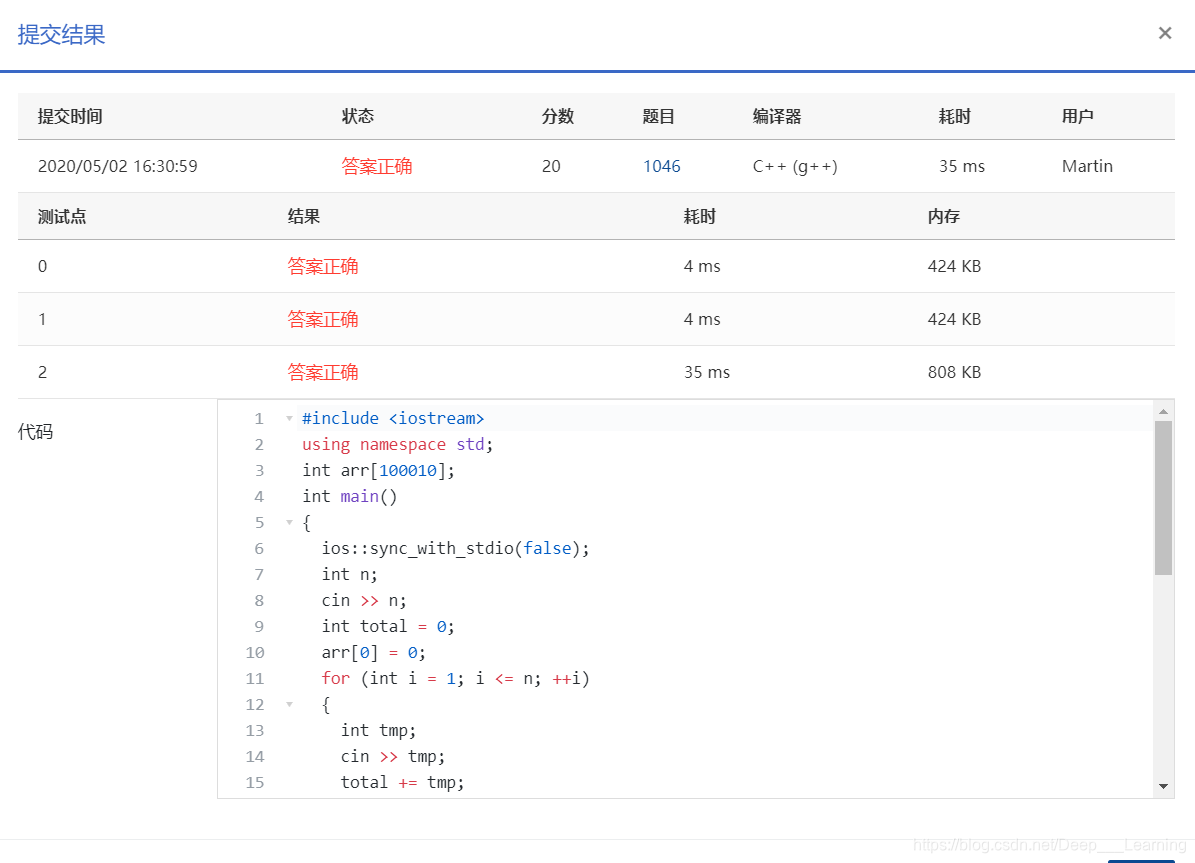
A与B之间的距离不就是A到原点的距离与B到原点的距离之差吗？而任意结点到原点的距离以及环的总长度，在输入的时候就可以求出来了。OK，懂了，这就写代码。(σﾟ∀ﾟ)σ…:*☆哎哟不错哦
在这里插入图片描述

AC代码

#include <iostream>
using namespace std;
int arr[100010];
int main()
{
	ios::sync_with_stdio(false);
	int n;
	cin >> n;
	int total = 0;
	arr[0] = 0;
	for (int i = 1; i <= n; ++i)
	{
		int tmp;
		cin >> tmp;
		total += tmp;
		arr[i] = arr[i-1] + tmp;
	}
	int m;
	cin >> m;
	for (int i = 0; i < m; ++i)
	{
		int a, b;
		cin >> a >> b;
		if (a > b)
		{
			int t = a;
			a = b;
			b = t;
		}
		int sum1 = arr[b-1] - arr[a-1];
		int sum2 = total - arr[b-1] + arr[a-1];
		cout << min(sum1, sum2) << endl;
	}
	return 0;
}